И снова за кривизну
Продолжим говорить о локальных кривизнах поверхности (ранее мы обсуждали измерение кривизны вдоль ребра). Свойства поверхности «в малом» опрашивает инструментальный класс GeomLProp_SLProps библиотеки OpenCascade. Он вычисляет главные направления и кривизны поверхности, а также среднюю и полную (гауссову) кривизны в данной точке $(u,v)$. На картинке ниже изображен сплайн и результаты измерений его кривизн в некоторой внутренней точке.
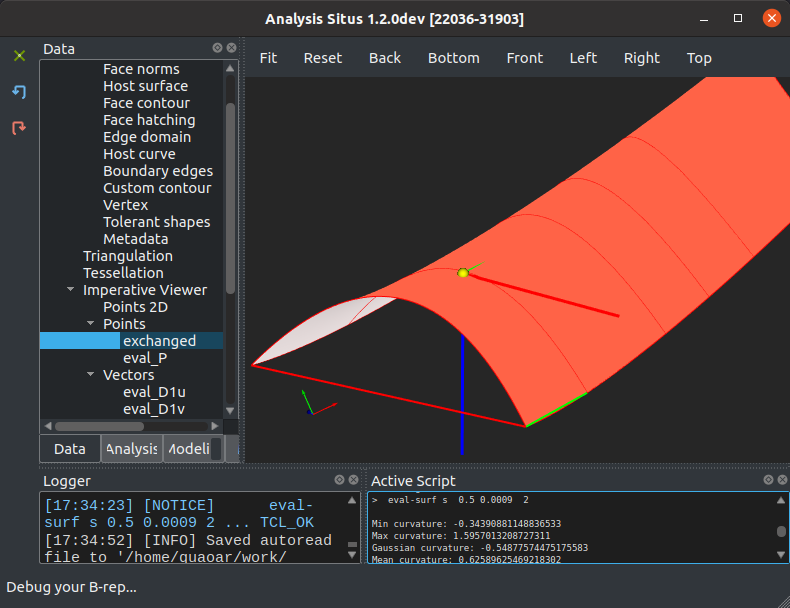 |
Сплайн-поверхность и ее кривизны в произвольной точке. |
Min curvature: -0.34390881148836533 Max curvature: 1.5957013208727311 Gaussian curvature: -0.54877574475175583 Mean curvature: 0.62589625469218302
Поскольку мы рассматриваем вычисление кривизн не абстрактно, а с позиций геометрического моделирования, большое значение приобретает также ориентация поверхности, то есть направление ее нормалей. Выбор параметризации поверхности в известном смысле произволен, однако направление нормали оказывает влияние на знак вычисляемых кривизн. Действительно, согласно определению, кривизна показывает насколько сильно нормальное сечение поверхности загибается по отношению к вектору нормали $\textbf{m}$ в данной точке (см. [Рашевский «Курс дифференциальной геометрии», пар. 57]. Ниже изображен лоскут седловидного сплайна, чья геометрическая ориентация изменена на противоположную. При этом значения кривизн также меняют знак (кроме значения главной кривизны).
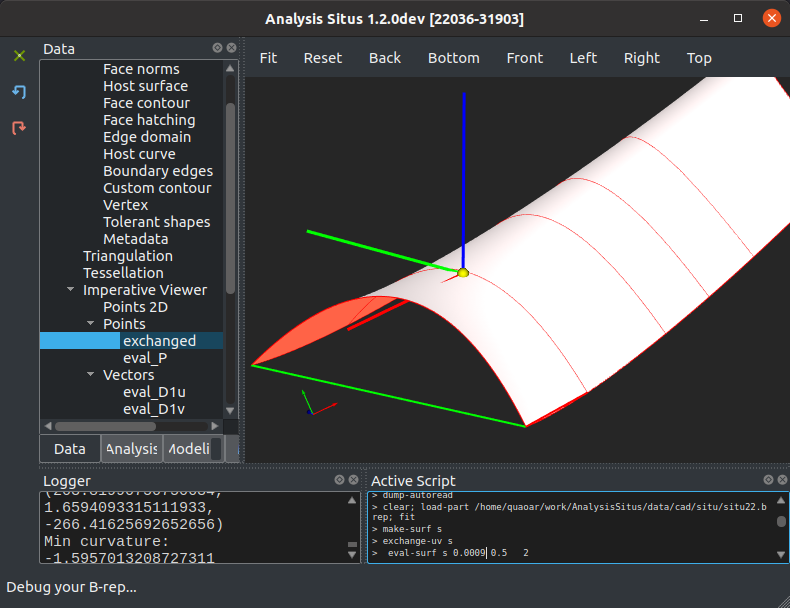 |
Инвертированная сплайн-поверхность. |
Min curvature: -1.5957013208727311 Max curvature: 0.34390881148836527 Gaussian curvature: -0.54877574475175583 Mean curvature: -0.62589625469218302
Знак кривизны становится существенным для определения локальной выпуклости или локальной вогнутости. Вогнутость поверхности может стать препятствием для изготовления соответствующей грани на станке с ЧПУ, поскольку она накладывает ограничение на максимально допустимый диаметр инструмента. Условно проблематичными можно считать все поверхности, имеющие локально гиперболический тип (гауссова кривизна отрицательна), а также поверхности с хотя бы одной положительной кривизной в силу своей топологической ориентации. Последнее обстоятельство в коде обыгрывается следующим образом:
double k1 = ...; // Max curvature.
double k2 = ...; // Min curvature
if ( face.Orientation() == TopAbs_REVERSED )
{
k1 *= -1;
k2 *= -1;
}
if ( k1 > 0 || k2 > 0 )
std::cout << "Surface is locally concave." << std::endl;
Таким образом, мы полагаемся на знак главных кривизн, имея в виду корректировку знака в связи с ориентацией поверхности. Заметим, что независимая проверка главных кривизн $k_1$ и $k_2$ позволяет отловить гиперболические, эллиптические и параболические точки одинаково хорошо. Мы полагаем здесь, что для объявления всей поверхности локально вогнутой достаточно положительной кривизны этой поверхности хотя бы в одном направлении в хотя бы одной точке. Действительно, наличие такого «дефекта» затрудняет производство детали, и здесь неважно, является ли поверхность вогнутой в малом или глобально.
Want to discuss this? Jump in to our forum.