Convert B-spline curves and surfaces to Bézier form
OpenCascade provides a range of tools to represent curves and surfaces in different but compatible ways. For example, a surface patch might have to be represented as C1 or C2 NURBS or a patchwork of CN Bézier surfaces depending on the capacities of the receiving software. One of such tools is the class ShapeUpgrade_ConvertSurfaceToBezierBasis aimed at turning B-spline surfaces into Bézier representation.
It is known from theory (see "The NURBS Book") that a B-spline curve or a surface can be turned into a piecewise Bézier representation quite easily. We only have to increase the multiplicities of all knots until G0 continuity is achieved. As a result of this repetitive knot insertion, the initial geometry falls apart onto the desired Bézier segments. This conversion, however, does not entail modifying the polynomial degrees of the Bézier segments used. It comes as an unpleasant surprise that OpenCascade does not support degree reduction, which is, by the way, one of the most fundamental NURBS modeling operators.
So, how can we lower the polynomial degrees of our splines? The OpenCascade community suggests to reapproximate the input geometry with a certain degree limit. This idea paraphrases what you can read in the official shape healing docs, where a dedicated tool is proposed for that purpose (it is ShapeCustom::BSplineRestriction). The problem with such an approach is that geometry approximation is proven to be a bad idea. Reapproximation may easily deform your shape, not to mention its fairly humble performance.
At the same time, we have no choice left, unless we go and implement something like A5.11 from the aforementioned "NURBS Book." With reapproximation employed, Bézier conversion of a spline curve can be achieved as follows:
// Split to Bezier.
Handle(ShapeUpgrade_ConvertCurve3dToBezier)
bzConverter = new ShapeUpgrade_ConvertCurve3dToBezier;
//
bzConverter->Init( curve, curve->FirstParameter(), curve->LastParameter() );
bzConverter->Perform();
//
Handle(TColGeom_HArray1OfCurve) curves = bzConverter->GetCurves();
// Reduce degrees by reapproximation.
std::vector<Handle(Geom_BSplineCurve)> bCurves;
//
for ( int i = curves->Lower(); i <= curves->Upper(); ++i )
{
const Handle(Geom_Curve)& bzSeg = curves->Value(i);
// Since in OpenCascade there is no function for degree reduction, we can only
// reapproximate each segment to achieve the desired degree.
GeomConvert_ApproxCurve approx(bzSeg, 1e-15, GeomAbs_C1, 1, 3);
//
Handle(Geom_BSplineCurve) bsplSeg = approx.Curve();
bCurves.push_back(bsplSeg);
}
// Concatenate curves.
GeomConvert_CompCurveToBSplineCurve concat;
//
for ( const auto& seg : bCurves )
{
concat.Add( seg, Precision::Confusion() );
}
//
converted = concat.BSplineCurve();
Here the input curve is represented with the curve variable. It is turned into a series of Bézier segments with the ShapeUpgrade_ConvertCurve3dToBezier utility provided by OpenCascade. Then, our idea is to lower degrees for each segment using the approximation algorithm named GeomConvert_ApproxCurve. Finally, once all segments are turned into 3-degree polynomials (i.e., Bézier), we concatenate them back into a sole curve with the help of GeomConvert_CompCurveToBSplineCurve utility.
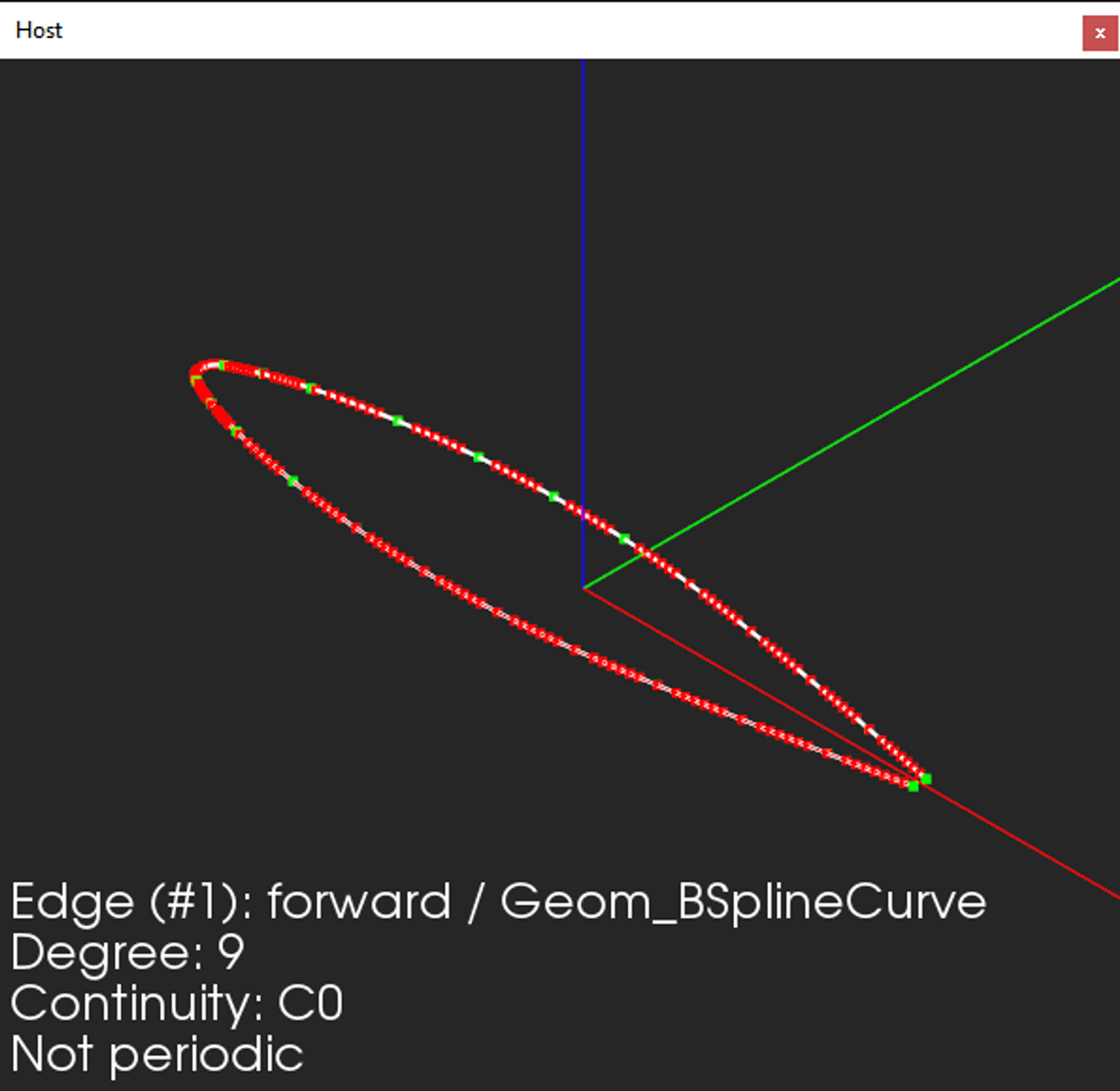 |
A curve before conversion (high degree, C0). |
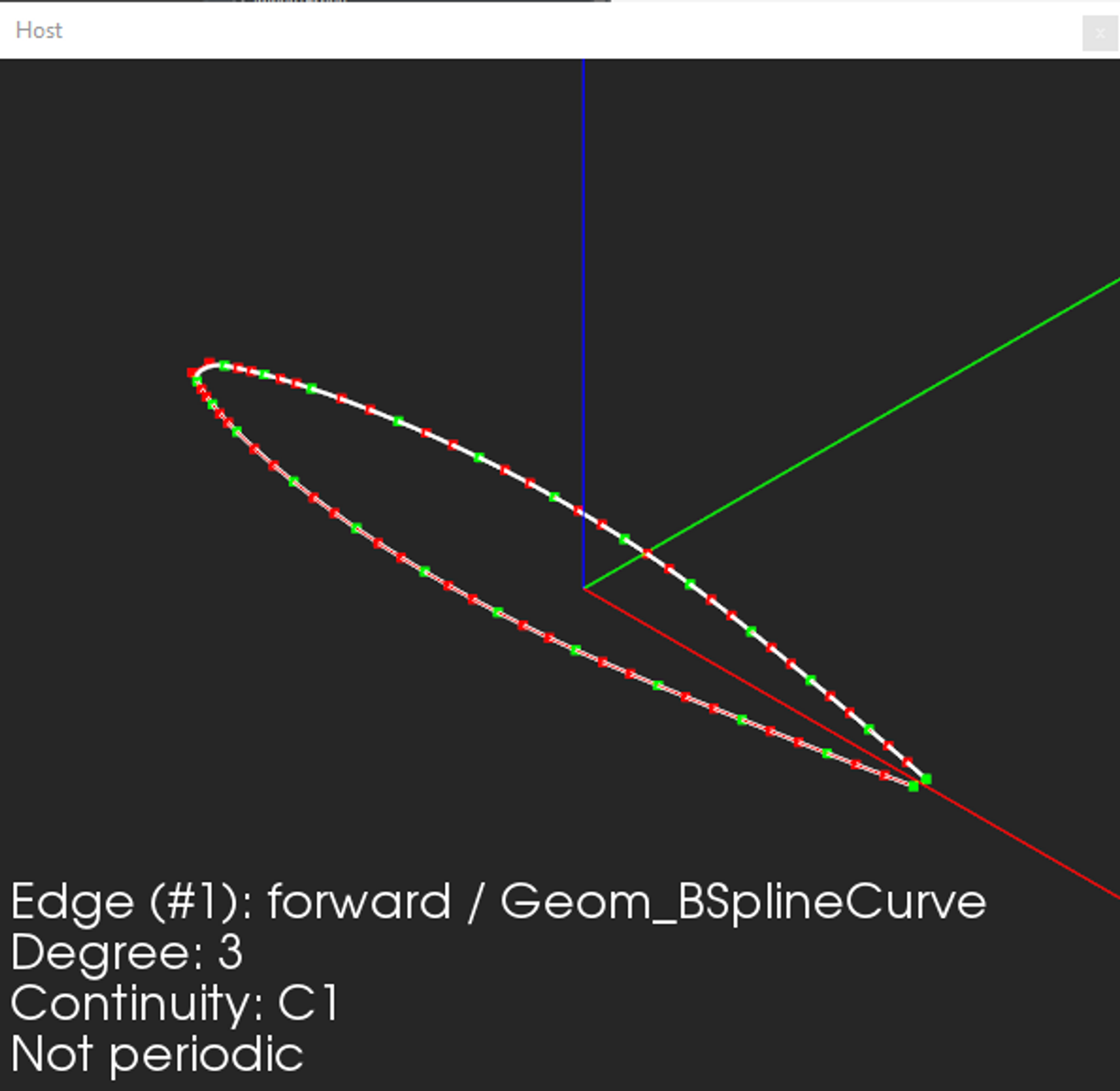 |
A curve after conversion (lower degree, C1). |
Surface conversion is a more difficult process. Degree reduction for surfaces, like curves, is not a simple algorithm. We break higher-degree spline surfaces into Bézier patches and then apply further processing to each patch separately.
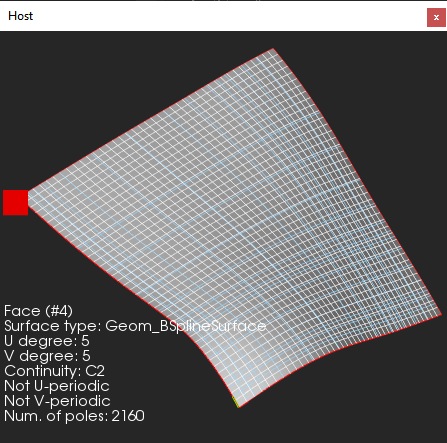 |
A surface before conversion (C2). |
If the initial surface is a 3-degree spline, we just need to make it C1-continuous. If the surface degree is higher, we must generally reapproximate each patch to achieve the necessary degree. Alternatively, we may just disregard some poles and construct a similar surface with degree 3, potentially adding more knots to reduce the influence of such a brute force conversion. The second variant is presented in the picture below:
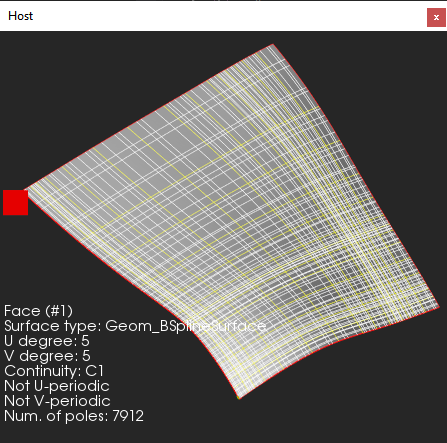 |
A surface after conversion (same degree, C1). |
If we utilize reapproximation, we get a true cubic spline while compromising accuracy.
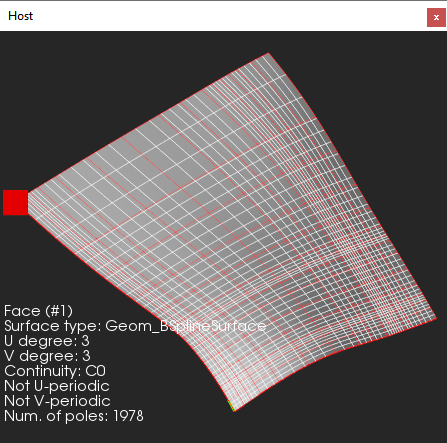 |
A surface after conversion (lower degree, C0). |
The described conversion capability, like many other surface modeling methods provided to Analysis Situs this year, is now open source.
Want to discuss this? Jump in to our forum.