A technical addendum to abandoned threads and HLR
 |
So, the proposed architecture of abandoned threads may seem OK if we have our application running indefinitely long and let the detached threads finish up whenever they like. The key motivation here was to keep our application responsive while background threads are bubbling up, no matter how slow they are. One implicit assumption here was that our application lives long enough for the detached threads to access the allocated resources of the owner process, so their execution "sandboxes" stay safe and sound.
The Trap
Let's imagine now that the process is being shut down while abandoned threads are still running. As we know, exiting a process (with return 0) implies killing all its threads, but that does not happen instantly. It may actually happen that a worker thread to be killed does some extra cycles on the shared data whose destructors have been just called. This is when darkness descends and SIGSEGV monsters randomly materialize here and there. The output in the stderr channel might look pretty much like this:
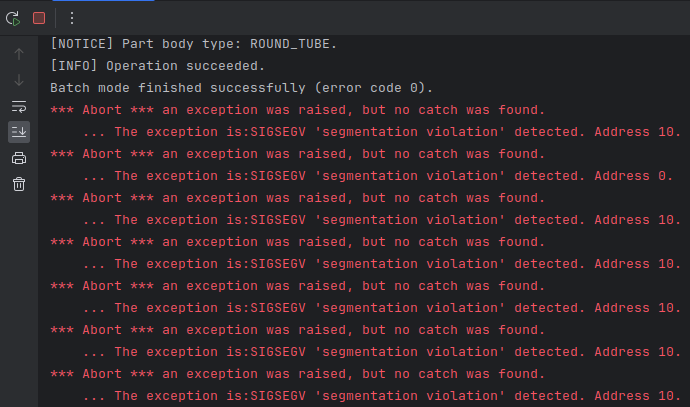 |
Notice that this happens at the very end, so the application pretty much did its job, but the abandoned threads mess everything up at the final moment. It is hopeless to debug such faults because they do not come from the broken algorithm's logic or imperfect data, so the occurrence of these faults is quite sporadic and conditional (may vary between release and debug, depend on context switching time, etc.). The process crashes because a thread is still alive while its data has already been released. The return code of such a process is not 0 (success) but something else:
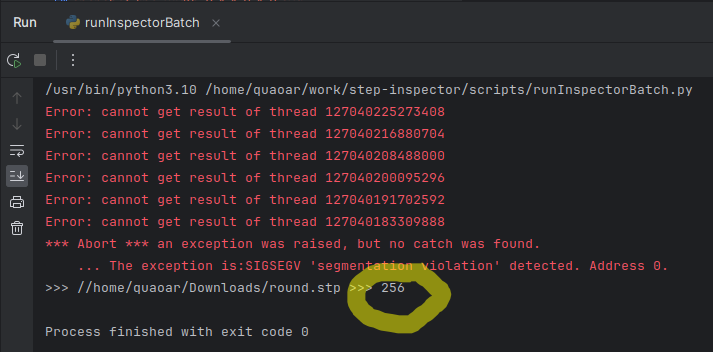 |
Trying to understand the frequency of this issue, I came up with the following little script in Python. It runs batch Analysis Situs (well, it's actually another commercial software derived from it) and prints out the return codes:
import os
import subprocess
data_folder = '../data'
install_folder = '../AnalysisSitus/install/bin'
logfile = '../scripts/log.txt'
outdir = '../out'
cmdname = 'xxx-perform'
timeout_s = 30
exename = install_folder + "/asiExe.sh"
open(logfile, 'w').close()
data_file_paths = []
for root, dirs, files in os.walk(data_folder):
if len(dirs) == 0:
data_file_paths += [os.path.join(root, file) for file in files if file[-3:] == 'stp']
codes = {}
for data_file_path in data_file_paths:
t = data_file_path.split(" ")
if len(t) > 1:
print("several tokens in filename, skipping...")
continue
arg = "'/runcommand=" + cmdname + " " + data_file_path + " " + outdir + "/outcome.json" + " -svg'"
print("arg: " + arg)
with open(logfile, "a") as outfile:
p = subprocess.Popen([exename, arg], stdout=outfile, stderr=subprocess.PIPE, text=True)
try:
p.wait(timeout_s)
except subprocess.TimeoutExpired:
print("Timeout " + arg + " sec. exceeded. Killing the process...")
p.kill()
retval = p.returncode
print(">>> " + str(retval))
codes[retval] = codes.get(retval, 0) + 1
for code in codes:
print ("code ", code,':',codes[code])
The procedure behind xxx-perform reads a STEP file and generates a number of HLR projection views to compose a PDF drawing later on. The Python script invokes Analysis Situs using the subprocess module and reads back the exit codes. The distinct exit codes are counted, so that we can check how many times the app finishes with a non-success state.
The tests have been conducted in the following computational environment:
CPU: Intel(R) Core(TM) i9-12900HX RAM: 32GiB Machine Type: Notebook OS: Ubuntu 22.04.3 LTS
For the reference, we start with the code base having no HLR enabled. The results are quite clean: just three faults where STEP files are somewhat broken and could not be read:
| Return code | Num. of cases |
| 0 (success) | 1727 |
| 1 (SIGSEGV or anything) | 3 |
Now, if we enable HLR with abandoned threads, the situation gets worse and some of the detached threads tend to crash at the very end of the process execution:
| Return code | Num. of cases |
| 0 (success) | 1690 |
| 1 (SIGSEGV or anything) | 37 |
| 134 (SIGABRT) | 3 |
We observe that 37 cases have crashed, while three more cases appear to have been aborted (why is unclear to me). To avoid these segfaults, all threads must finish their jobs when the process terminates. We need to inform them to be ready for graceful death, but it's difficult because these threads are detached and we have no control over them. An architecturally sound solution would be to flag the shared data such that a worker thread is notified of the termination event, allowing it to complete its thread function earlier. However, this is not an option when a worker thread executes third-party code, such as infinite HLR logic, Boolean operations, meshing, you name it. You cannot flag the data that you do not own. One alternative I considered was the OS-dependent API for forcibly canceling an abandoned thread. I.e., using the pthread_cancel() posix function.
As one can find out reading the documentation, the pthread_cancel() function sends a cancellation request to the specified thread. If a thread is marked with the PTHREAD_CANCEL_ASYNCHRONOUS cancel state, then, according to the documentation, this thread can be canceled at any time (usually immediately, but the system does not guarantee this).
The situation with the tests changes slightly when thread cancellation is enabled. First, some formerly successful runs are now classified as aborted. This would have been normal if SIGSEGV failures had been eliminated, but that does not appear to be the case. Instead, we find that some of the cases with the former 0 exit code now return 134, but the failing cases continue to fail no matter what.
| Return code | Num. of cases |
| 0 (success) | 1660 |
| 1 (SIGSEGV or anything) | 39 |
| 134 (SIGABRT) | 31 |
Eventually, this situation started to smell like a real trap. There is not much you can do when a thread function freezes in the code you can't control and the operating system fails to respond appropriately. It should be pointed out that a non-zero exit code is probably not going to be a show-stopper. Indeed, because these sporadic crashes occur at the end of the process, the application has essentially completed its task, and you can simply ignore the return value and collect the application's outputs. Still, I doubt you'd want to compromise on your application's return code. Not at all. It feels pretty much like putting a good deal of "goto" statements in the code, if not worse. Just haram. Period.
Copy & Paste & Waste
The conceptual problem of HLR is that it has never been finished by Matra Datavision. It is incomplete and the chances to see it finished and polished are equal to zero. This story just got too old. Unfortunately, copying and pasting the OpenCascade sources just to be able to use an otherwise unstable algorithm is becoming a usual practice for us. It breaks my heart but I found myself copying and pasting yet another hundred of source files to Analysis Situs to be able to patch it the way I need. Now, instead of talking about nice and cool algorithmic nuances of HLR, I will tell you how to copy & paste successfully.
Look here:
#define ThePSurface Standard_Address #define ThePSurface_hxx <Standard_Address.hxx> #define ThePSurfaceTool HLRBRep_SurfaceTool #define ThePSurfaceTool_hxx <asiAlgo_HLRBRepSurfaceTool.h> #define IntCurveSurface_Polyhedron HLRBRep_ThePolyhedronOfInterCSurf #define IntCurveSurface_Polyhedron_hxx <asiAlgo_HLRBRepThePolyhedronOfInterCSurf.h> #include <IntCurveSurface_Polyhedron.lxx> #undef ThePSurface #undef ThePSurface_hxx #undef ThePSurfaceTool #undef ThePSurfaceTool_hxx #undef IntCurveSurface_Polyhedron #undef IntCurveSurface_Polyhedron_hxx
This is something you'll have to put into your project together with tons of other legacy code if you choose to copy & paste stuff. Whenever you come across lxx file extension be aware that such files declare inline methods. It essentially means that you should keep these methods defined right in the header file as otherwise you risk to lose the corresponding symbols from the finally cooked dynamic library. Look at these functions whose definitions I incorrectly moved to the cpp file while keeping inline qualifier:
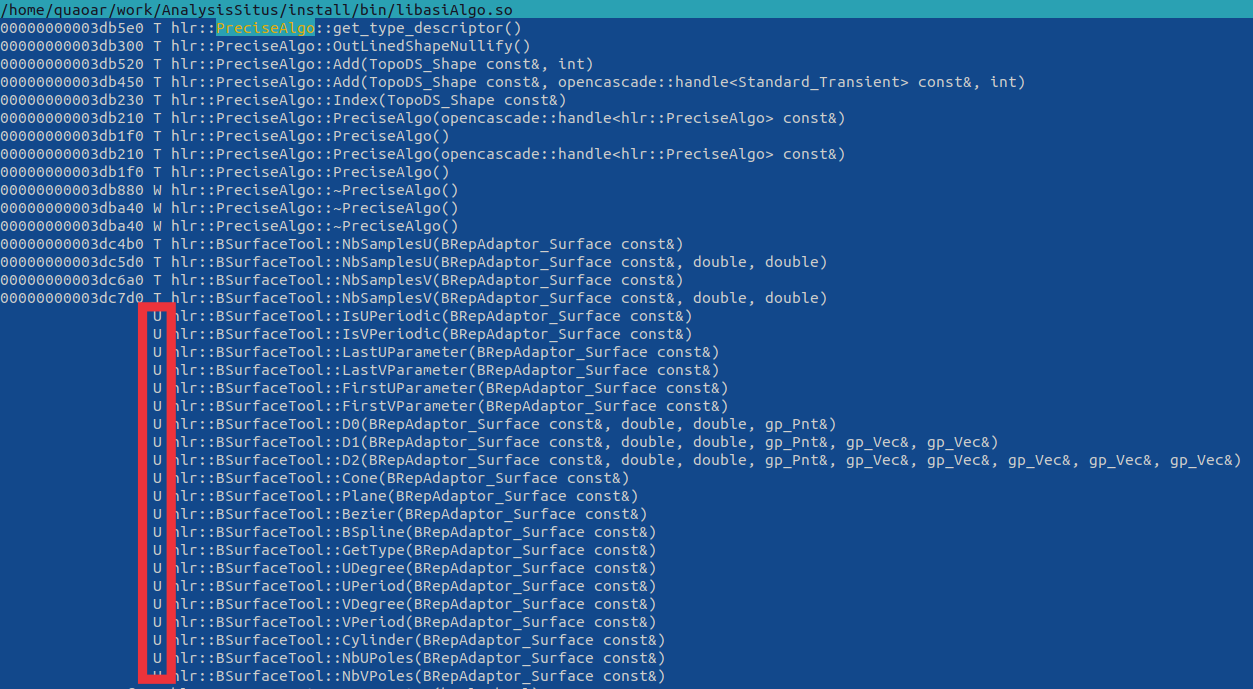 |
They all got wiped out, so I ended up with quite a bunch of weird linker errors. Also, you may wonder why this include statement is surrounded with all these strange macro definitions like ThePSurface, etc. This mystery is called "generics" in OpenCascade. The idea was to have something like C++ templates, i.e., parameterized types, back in times when templates were not broadly supported. Unfortunately, this mechanism would only work if you don't have namespaces in your class names. If you add namespace for your classes and keep using generics, the macro substitution will end up in syntactically broken code. Apparently, all generic classes of OpenCascade have to be remastered with the use of C++ templates to provide better reusability and ease debugging.
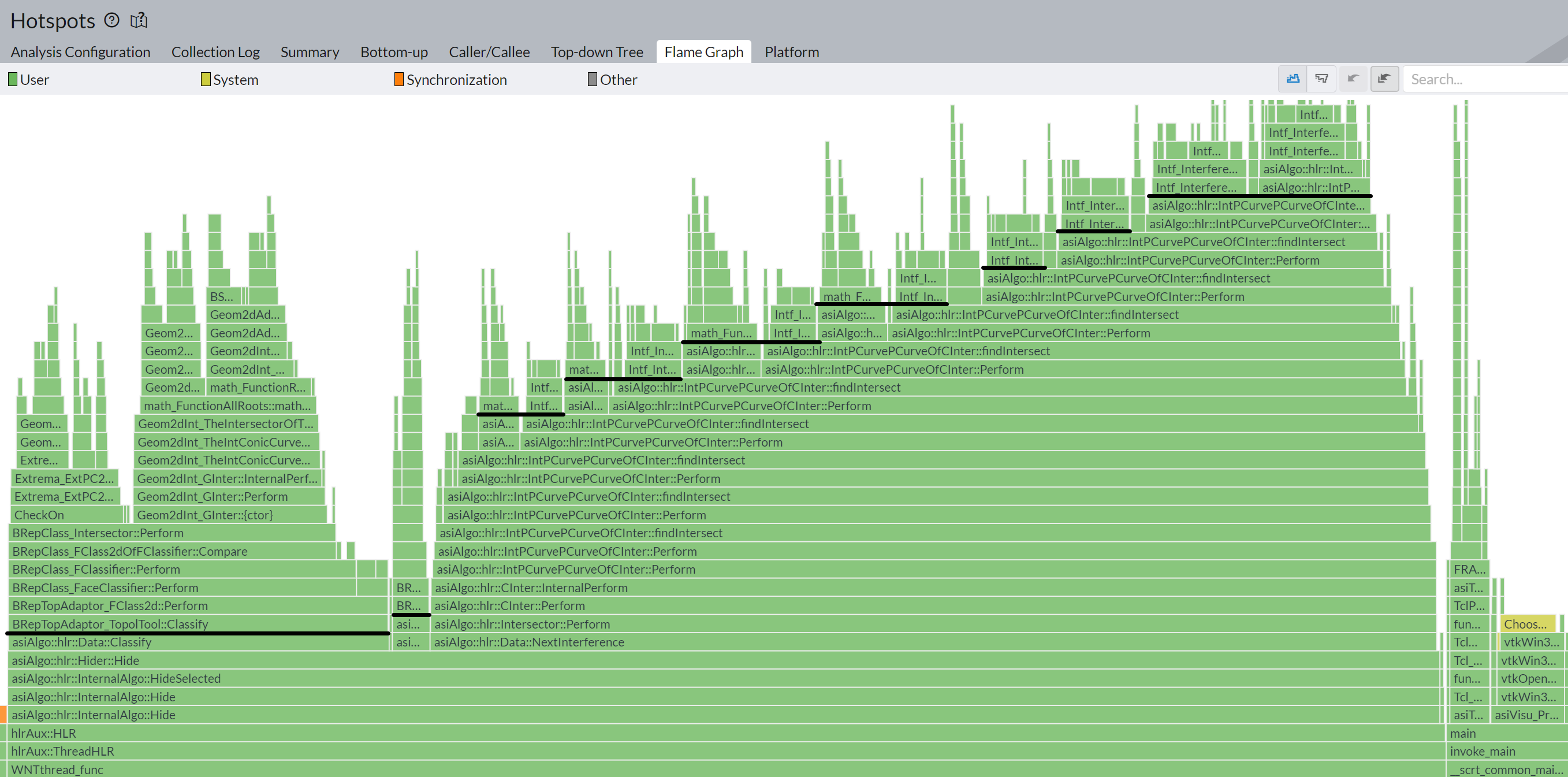 |
In the flame chart above, you can see how the forked HLR algorithm distributes its work among several internal classes. Almost entire work is being done in the "Hider" class (originally HLRBRep_Hider), so this is essentially where we can inject our cancellation instructions. If abandoned threads are canceled right after they exceed the time limit, the situation with segmentation faults becomes much better:
| Return code | Original | Fork |
| 0 (success) | 1708 | 1727 |
| 1, SIGSEGV, SIGABRT, timeout | 23 | 4 |
The injected cancellation mechanism is sort of "polite," i.e., the abandoned thread is informed that the caller code asks it to finish. Then it is up to the thread to continue working up until the next cancellation point in the code, and the trick is to check the cancellation condition as frequently as possible.
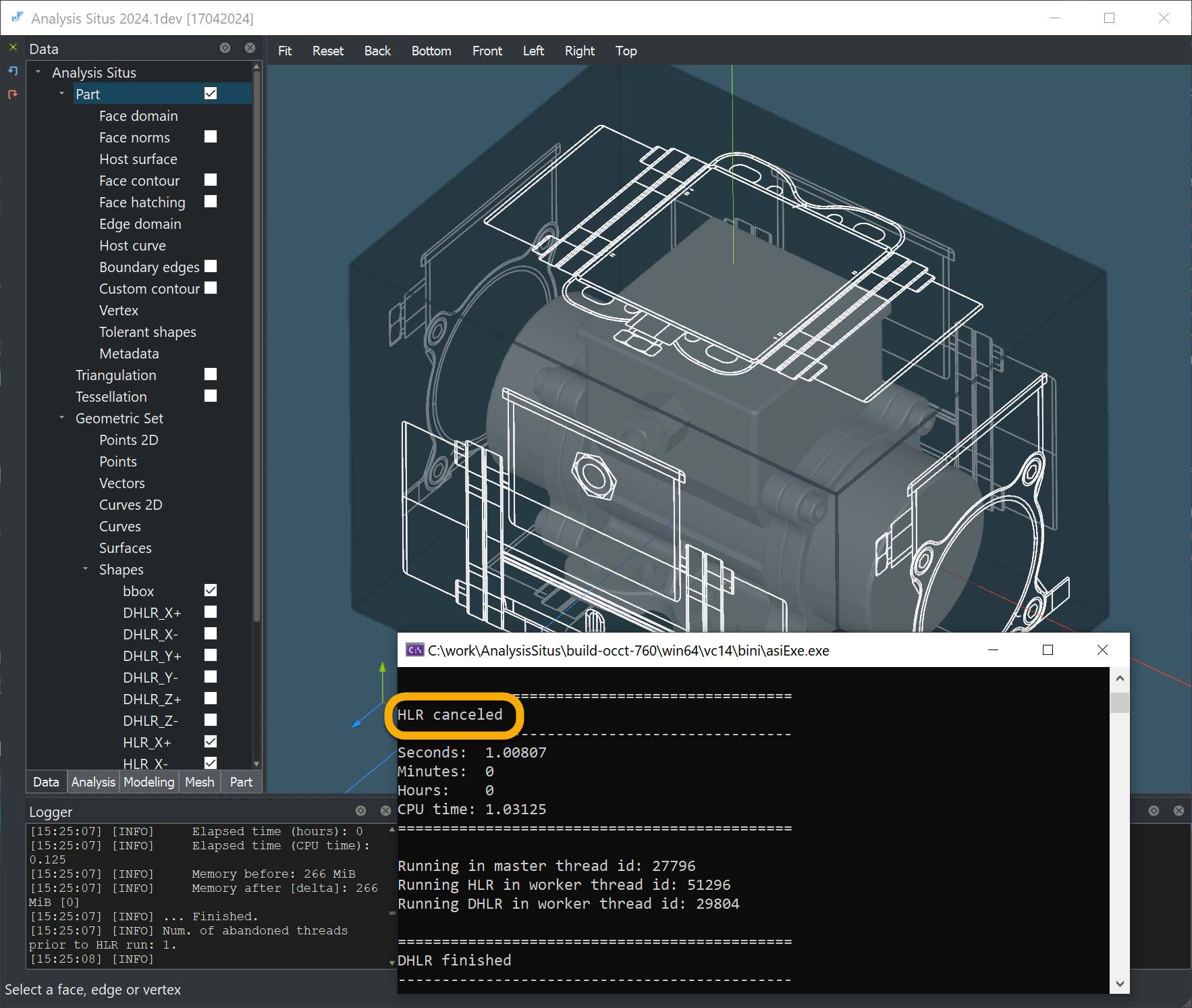 |
In reality, to properly patch HLR, you do not need to copy and paste its complete source code. We ended up altering only four classes in the hopes that one day the HLR algorithm will get an improved execution control, allowing us to securely discard all of these dirty changes.
Want to discuss this? Jump in to our forum.