Concatenate pcurves
Overview
As practice proves, it is often challenge to prepare an existing geometry to finite element simulation, because such preparation inevitably requires quite delicate manipulations with curves and surfaces. Our team has got an opportunity to develop quite a couple of things in the open source Analysis Situs to streamline CAD preparation workflows in a plenty of ways. In this and the following articles to be published over 2023, we are going to touch on different aspects of shape simplification, adaptation and idealization. Such operations are normally aimed at getting the possibility to run other software packages that pose their own specific requirements on the input geometry. Sometimes, it is not simplification as such but a somewhat trickier shape morphing that might remain invisible for a human being but makes a lot of sense computationally.
The topic for today is the concatenation of edges. This operation aims at reducing the number of trimming curves surrounding the CAD faces and, this way, making the boundary representation cleaner. We have already spoken about a somewhat similar functionality, but it was a global operation whose effects are hard to predict. In this and the following articles, we do not require geometric operators to be fully automatic anymore. If guided by the user, such operators have better chances to bring the desired outcome.
 |
P-curves selected for concatenation. |
Let's assume we have just a couple of edges to join. If we know how to concatenate a pair of adjacent edges, then we can reuse the implemented logic for an edge chain of arbitrary length. The first step would be identifying which of the passed edges is the first one and which one is the second. Such a check should employ special treatment for orientation as the orientation swaps the order of start and end points in an edge. Also, we assume that the user selects pcurves in the Domain Viewer of Analysis Situs rather than the 3D edges in the modeling space. That's simply because selecting unstitched 3D curves would be ambiguous: there are two edges in the same location but belonging to different faces.
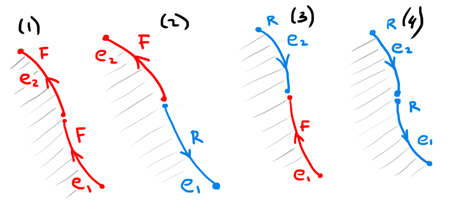 |
Four different cases for a pair of adjacent edges. |
The indexation of edges and thereby the choice of e1 and e2 can be based on the local indices of these edges in their owner contour. In a good contour, the edges are ordered following their topological connectivity.
 |
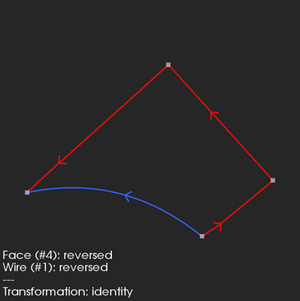 |
Example 1. |
 |
 |
Example 2. |
Lessons learned
The concatenation is largely done by the OpenCascade kernel itself but the hard thing is always making it work as expected. Let's omit pure mechanics here as you can always consult the sources of asiAlgo_JoinEdges, where we have it all put together. Instead, we'll list a couple of interesting details revealed during the implementation process.
How to update a contour?
Once the selected edges are merged, their owning contour needs to be updated. We followed a lazy road here and tried to compose another wire using a tool named ShapeExtend_WireData. The thing about this tool is the simplicity of use. Instead of composing a contour in the order of connectivity, you just put all the edges into an unordered collection and let the tool figure out how to permute the edges. Well, as practice proved, no permutations would happen automatically as this tool is simply not designed for that.
 |
Unexpected connectivity issues at vertices due to the broken order of edges in a wire. |
You have two options for obtaining the constructed contour from ShapeExtend_WireData: call its Wire() or WireAPIMake() methods. When the Wire() method is used, the constructed contour has the same edge order as the ShapeExtend_WireData tool. As a result, because the OpenCascade's validity rules require that topologically connected edges follow one another, we could easily end up with a broken wire. To repair the wire after construction, we'll have to apply the following function (notice the FixReorder() modifier in the chain):
//! Restores the validity of the passed wire.
TopoDS_Wire FixWire(const TopoDS_Wire& W,
const double tol)
{
ShapeFix_Wire wireFixer;
wireFixer.Load(W);
wireFixer.FixReorder();
wireFixer.FixClosed(tol);
wireFixer.FixGaps2d();
wireFixer.FixConnected();
return wireFixer.Wire();
}
Another method for obtaining a wire from ShapeExtend_WireData is via its WireAPIMake() method. The difference between this method and Wire() is in how the final contour is built. While Wire() can return topologically invalid contours (which must be corrected later on), WireAPIMake() tries to be more consistent by placing the edges as they go geometrically. The issue here is that any misordered edges will be skipped, resulting in large gaps in the final contour. Still, this method has a significant advantage over Wire(): by constructing the edges with OpenCascade's API, we ensure that their vertices are stitched together and the contour is perfectly manifold.
To summarize, it is critical to ensure that the edges are added to ShapeExtend_WireData in the correct order, and then use the WireAPIMake() method to obtain the closed contour.
Seeeeeewing
What has been discussed thus far is intended for a single CAD face. In practice, however, you're more likely to be dealing with shells and solids. The bad news is that if you stitch the corresponding face with another where pcurves haven't been merged, all merged pcurves will be split again. This is not surprising behavior, and it would be the same in Catia. To overcome this effect, the following simple procedure can be employed:
- First, concatenate pcurves in each face separately. The affected faces will be topologically detached from their neighbors automatically at this point.
- Stitch faces back together with a prescribed tolerance.
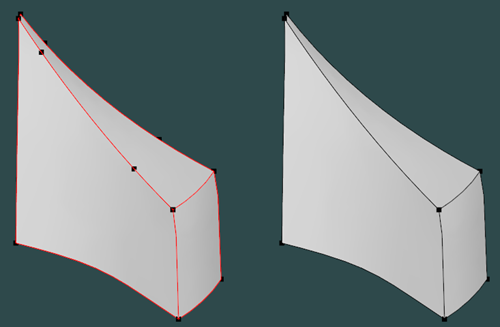 |
Refined and stitched model. |
The image above shows how an unordered set of faces with excessive topology was simplified into an eight-verticed, twelve-edged hexahedral body homeomorphic to a cube. That is exactly what we are looking for when partitioning a model prior to hexa meshing.
Surfaces with angular dimensions
Surfaces of revolution as well as cylinders and cones are hard to manipulate with in the Domain viewer, because they have an angular curvilinear axis defined in radians. Visually, such domains are tall and narrow, thereby selecting the pcurves of interest and even understanding their mutual configurations becomes a pretty annoying fuss.
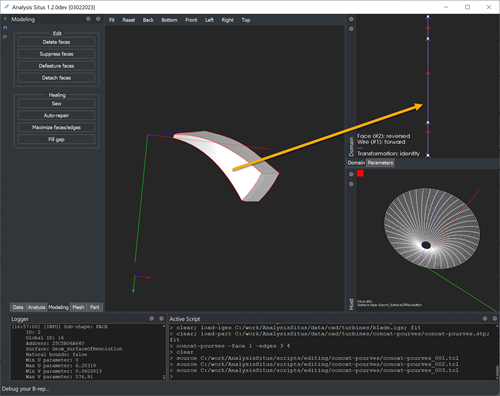 |
Surfaces of revolution are hard to manipulate in the UV domain because the U coordinate is not metric (it's the angle defined in radians). |
To ease the end user's life, we have introduced a long awaited function of temporary UV scaling. By pressing the <U> and <V> keyboard buttons, the user is able to scale up the corresponding dimensions of the parameters portrait and this way make pcurves better selectable.
 |
U/V scaling. |
Internal instancing
A while back, we discussed the B-rep instancing effect, which appeared to be quite an unpleasant thing to discover. The good news was that face instancing would magically fade away on STEP import/export, so you do not necessarily have to worry about it. But. Recent experiments have revealed that some strange instancing may appear on STEP translation when you least expect it. To get such weird surprises, you just need to save a shell to the STEP file and read it back. Viola:
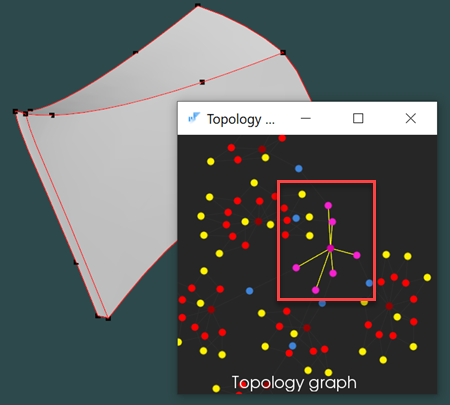 |
You wouldn't want to see those yellow links, I promise. |
By element instancing we understand the situation when a boundary element is associated with a transformation matrix right within a single part. Because the original model was a compound, it may have been handled as an "assembly" during STEP translation (that would explain some transformation matrices popping up on individual faces). These matrices are not only meaningless (they are all identities), but they also significantly complicate computations. We now have to pass the corresponding locations every now and then, keeping in mind that those locations are generally different objects even if their values are just identical (OpenCascade would have probably benefited if these matrices were manipulated by value). The consequences of ignoring locations when you're not supposed to are difficult to articulate. To give an example, you will end up with crashes everywhere for no apparent reason, such as because a located edge could not be found on a surface without the corresponding location.
The fix for this issue often consists in forcibly nullifying transformations associated with faces. That might make your code look a bit ugly, but that's the reality we must accept.
How to use it
> concat-pcurves -face 1 -edges 3 4
Want to discuss this? Jump in to our forum.