Optimal part orientation
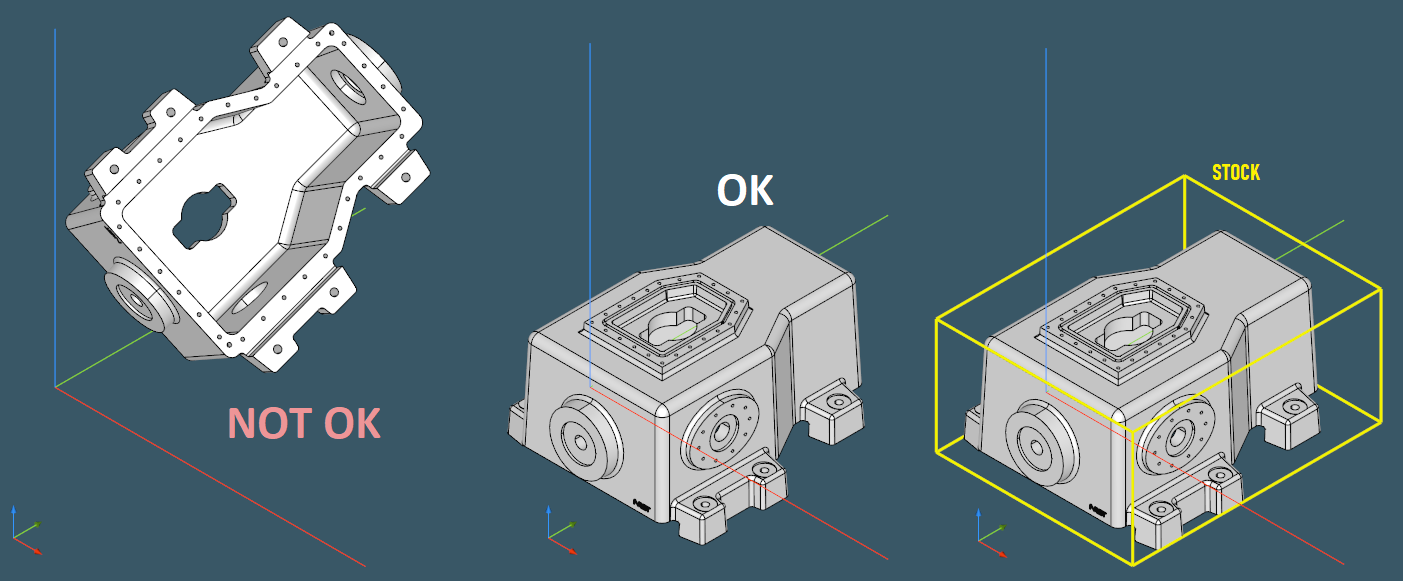
Volume decomposition techniques for feature recognition require a part to be properly oriented relative to a stock. As we'll be paying more attention to volume decomposition techniques, it seems right to talk about proper part alignment. Below are some examples of the parts whose positions leave a lot to be desired:
 |
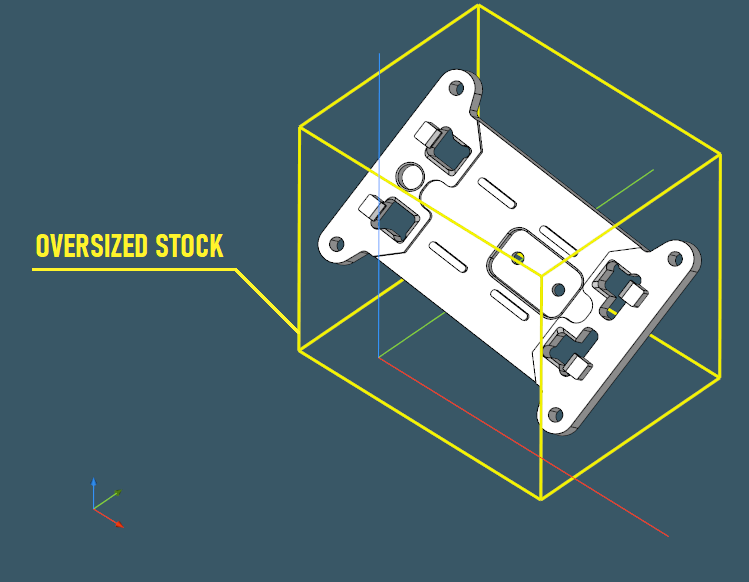 |
When a solid is imported from a CAD file, it may be placed anywhere in the modeling space. In the majority of cases, a part will be aligned with the global axes because that is how people design. In rare situations, however, a part may be exported from an assembly arrangement with a custom location that is not always aligned with X±Y±Z±. In such cases, a part must be repositioned to better match the hypothetical stock shape.
 |
Let's present a simple strategy that we believe is highly efficient for finding the optimal position of a part. The algorithm can be briefly outlined as follows:
- Realign the part using its symmetries along the OZ axis (orient-part Tcl command).
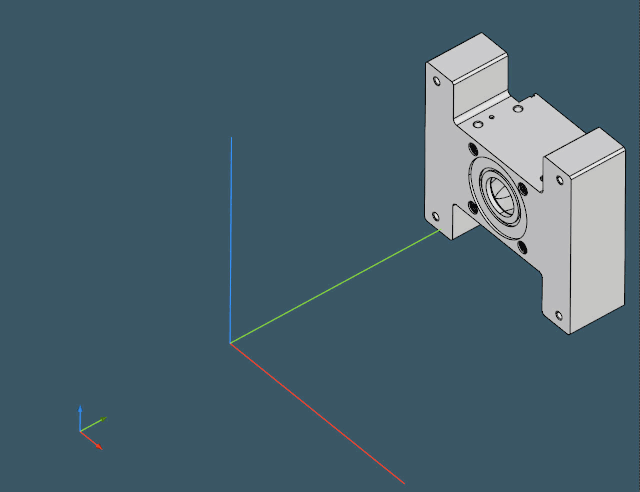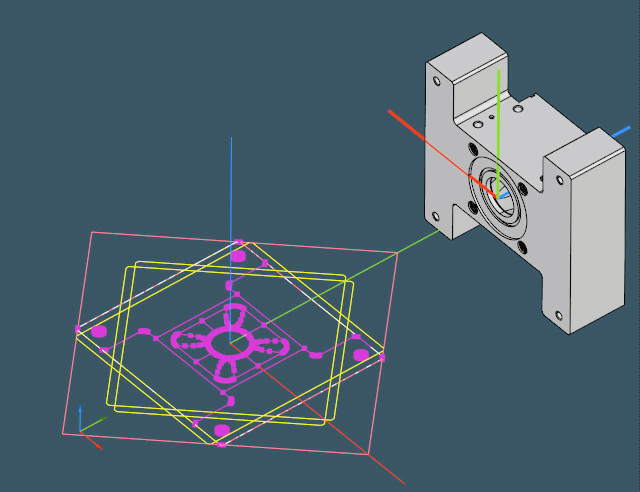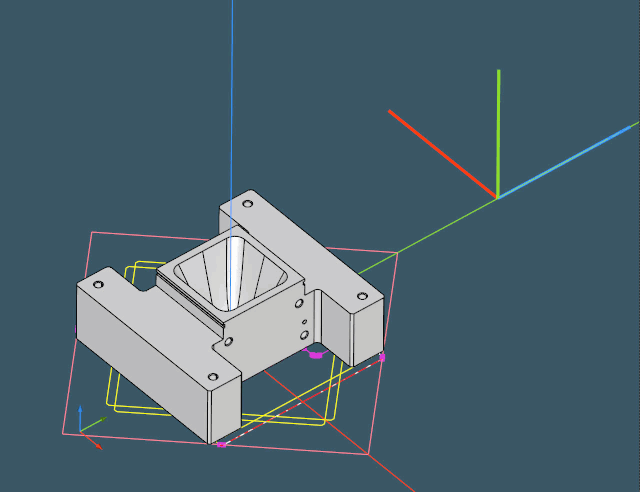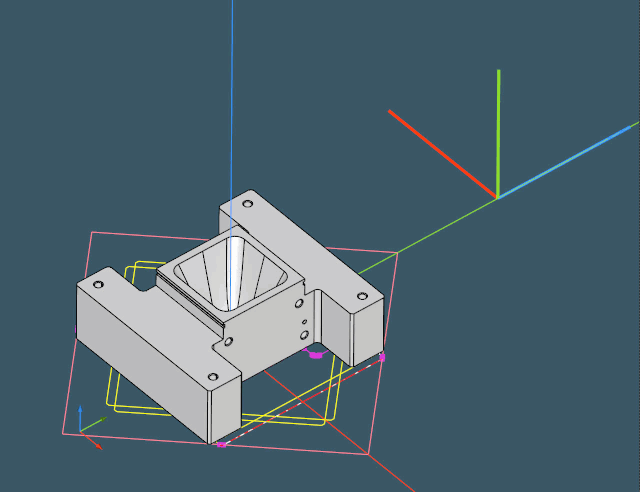
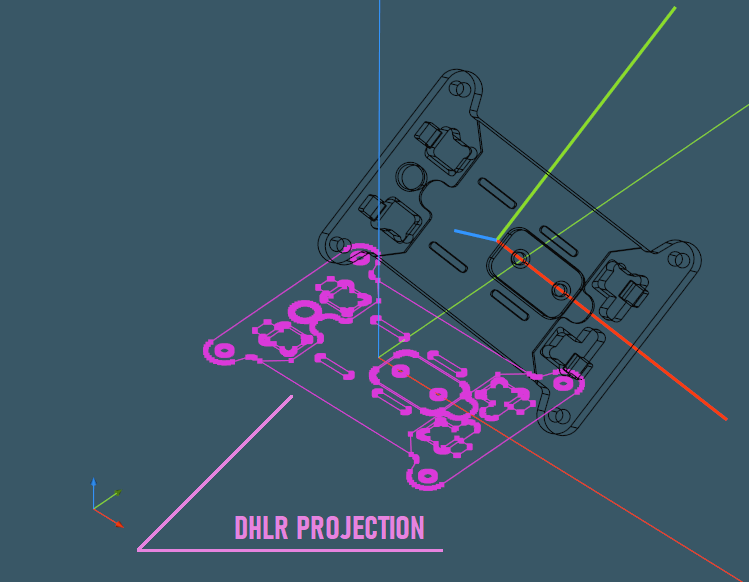
- Use DHLR to project the part onto XOY.
- Build a two-dimensional convex hull of the projection.
- In a manner similar to the "rotating calipers" method, find the minimal area rectangle over the convex hull.
- Rotate the part around the OZ axis at the computed angle.
 |
The first step is a somewhat "feature recognition junior." Instead of trying to identify all machining features in the model and orient the part properly (which should be done eventually for setup planning), we rely on surface normals and axes as feature hints. The objective is to calculate the overall "gravity" of each intrinsic axis in a part and select the most "significant" axis as the new OZ orientation. Fair, easy, and quick. As a result, we obtain the movable axis frame baked into the part:
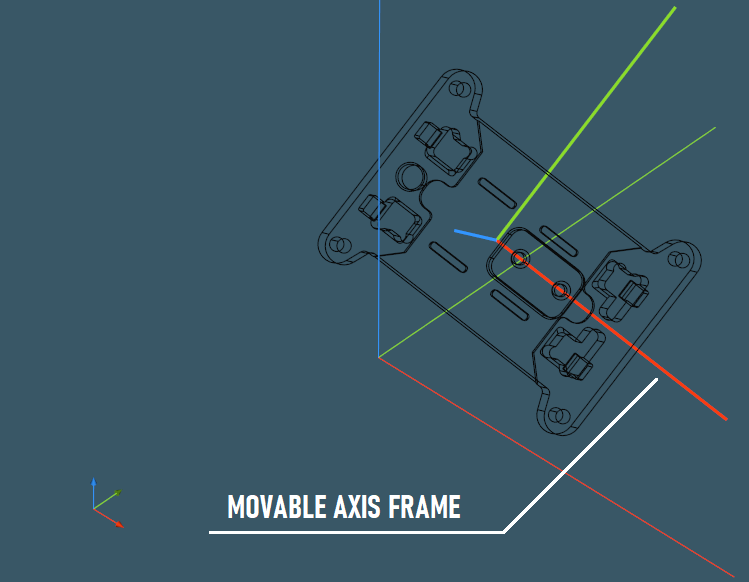 |
This frame can now be used to realign the part with the global OZ axis, and this way we get rid of one dimension in our three-dimensional relocation problem. Once done, we can project the part onto the XOY plane for further assessment.
 |
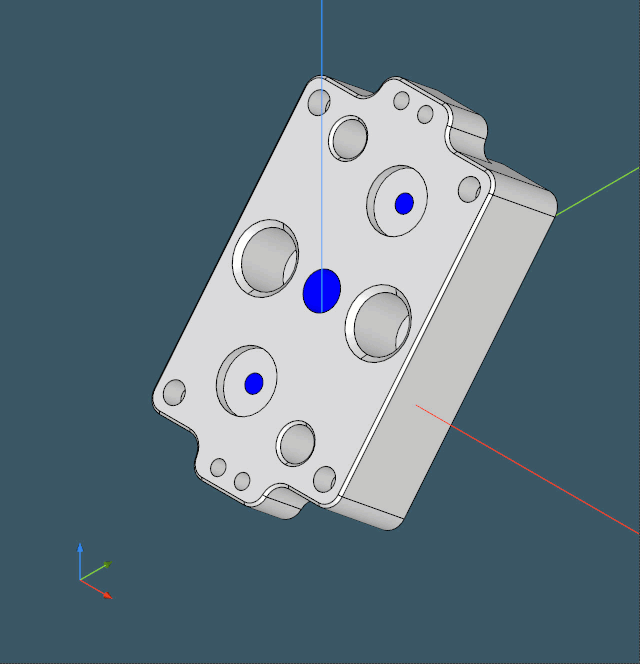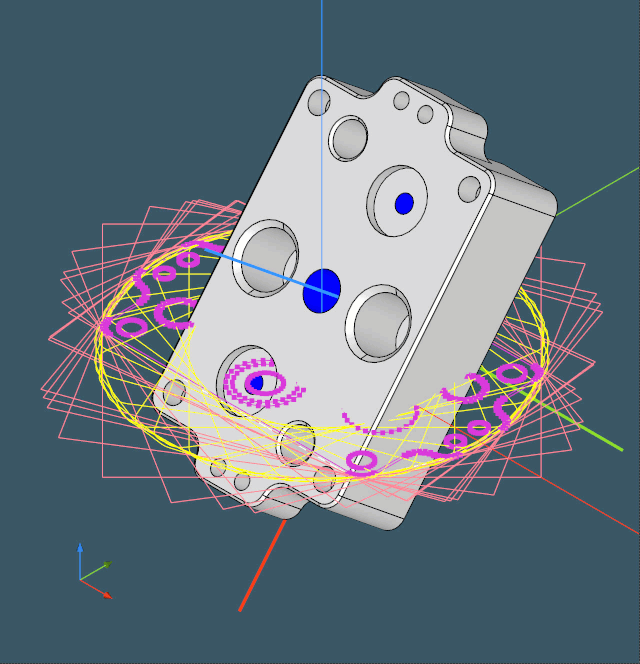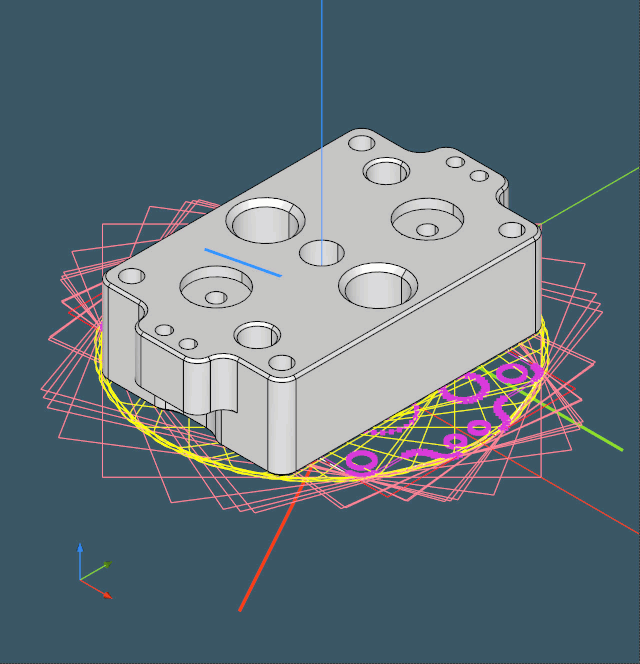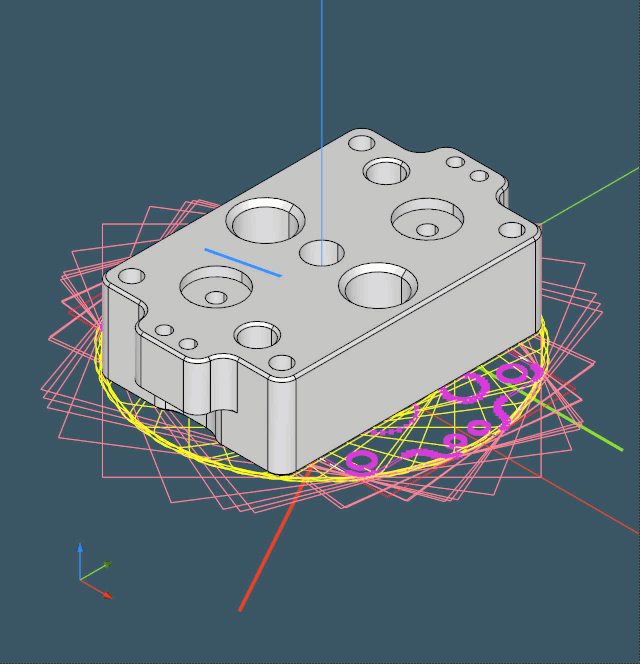
The next stage is to construct a two-dimensional convex hull, as we're going to use its segments for "calipers."
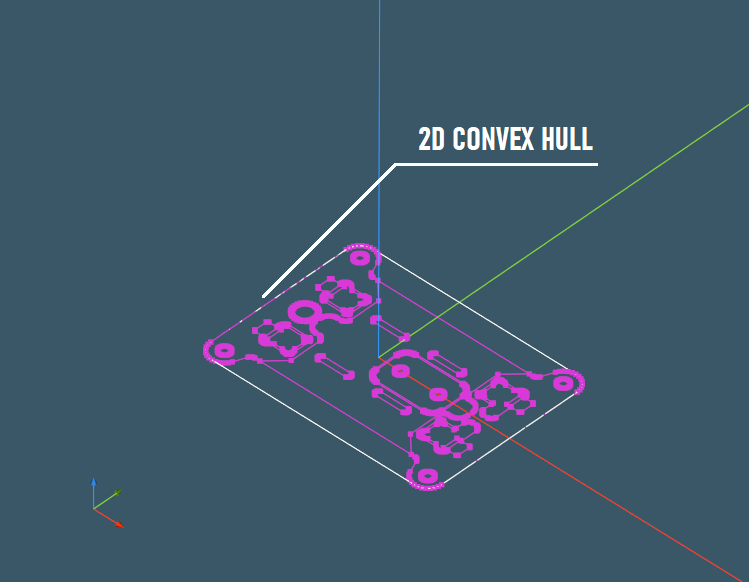 |
The algorithm then iterates all the straight edges of the convex hull and estimates the area of each bounding rectangle. The best one is chosen together with the corresponding rotation angle around the OZ axis.
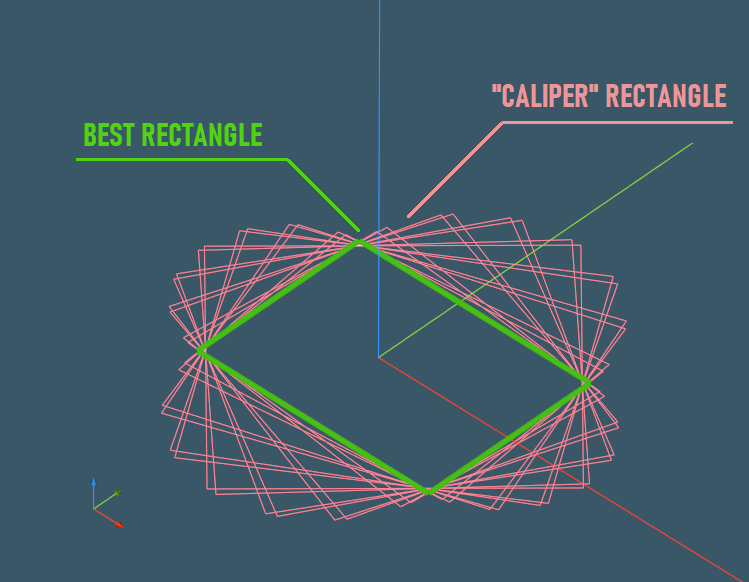 |
This algorithm is simple yet efficient, given that all steps are properly implemented. For example, it is critical to employ DHLR instead of precise HLR in order to quickly get the projected view of a part that we can subsequently rotate.
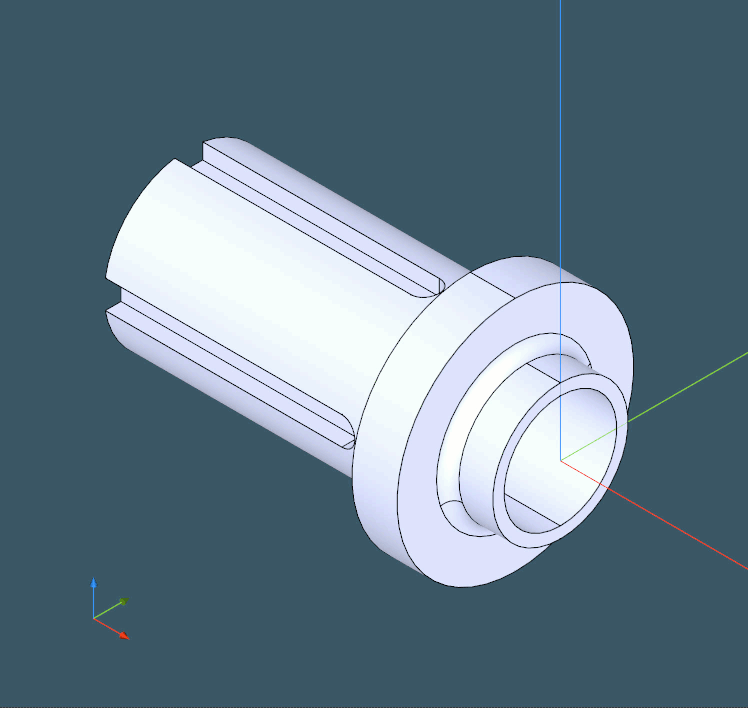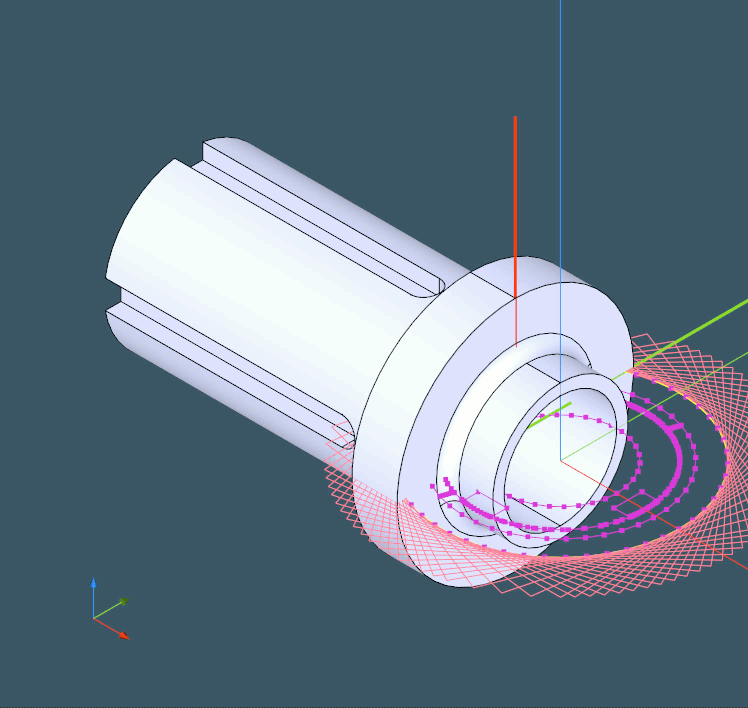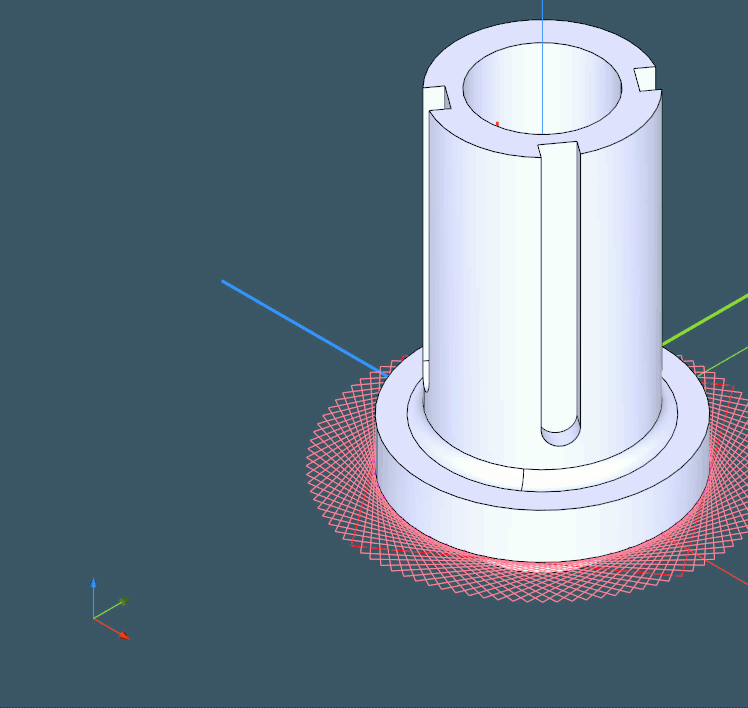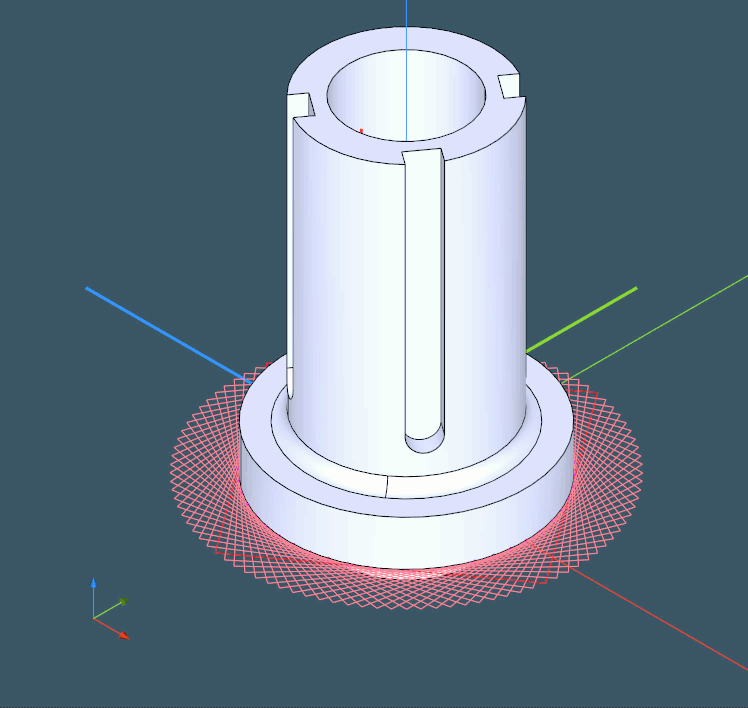 |
Once the part is positioned within a stock, it's time to proceed with volume decomposition, but that is another story which we leave for another day.
Want to discuss this? Jump in to our forum.