Кривизна грани вдоль ребра
«In order to begin an analysis, there must already be a synthesis present in the mind». Йохан Хёйзинга.
В этой короткой заметке мы дадим некоторые сведения по вычислению кривизны поверхности вдоль произвольной кривой при помощи библиотеки OpenCascade. Дело в том, что API библиотеки дает доступ только к «классическим» дифференциальным свойствам, таким как гауссова и средняя кривизны, а также их компоненты — главные кривизны и направления. В большинстве приложений этого достаточно, но бывает, что необходим и более тонкий анализ. Вопросы подобного рода задавались на официальном форуме OpenCascade, поэтому будет нелишним данную тему «подраскрыть».
Для вычисления свойств поверхности «в малом» OpenCascade предоставляет инструментальный класс BRepLProp_SLProps (B-Rep Local Properties / Surface Local Properties). На вход подается точка параметрического пространства поверхности (u, v) и сама поверхность, дифференциальные свойства которой подлежат расчету. Напомним, что дифференциальная геометрия поверхности в классическом изложении начинается с введения кривой, лежащей на этой поверхности — CONS (Curve ON Surface, рис. 1). Изучение дифференциальных свойств этой кривой позволяет вывести дифференциальные свойства поверхности, и, прежде всего, ее первую и вторую фундаментальные формы. Мы говорим здесь об этом потому, что коэффициенты фундаментальных форм дадут нам возможность рассчитать кривизну поверхности для произвольного направления в ее параметрическом пространстве. Повторим кратко основные положения теории, чтобы было проще перейти к реализации.
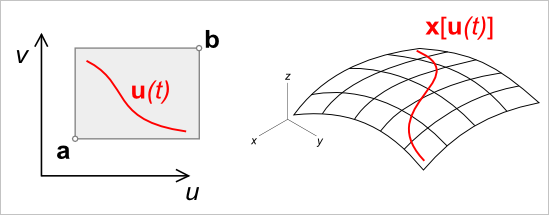
Рис. 1. Кривая на поверхности в параметрическом пространстве (слева) и пространстве моделирования (справа).
Изучение метрических свойств кривой приводит к первой фундаментальной форме. Если ds — это элемент дуги кривой, то коэффициенты первой фундаментальной формы имеют следующий вид:
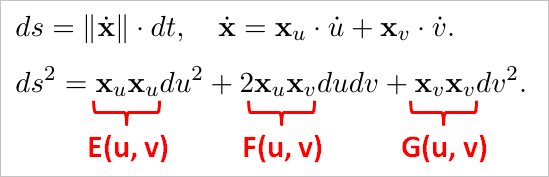
Коэффициенты E, F и G называют метриками поверхности. Изучение кривизны CONS приводит ко второй фундаментальной форме, коэффициенты которой принято обозначать как L, M и N.
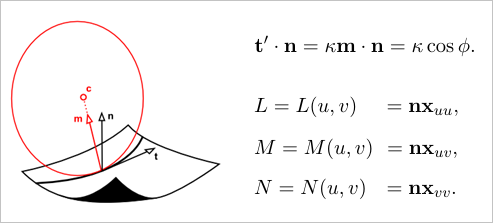
В теории доказывается теорема Мёнье, которая гласит, что кривизна любой кривой на поверхности может быть выражена через нормальную кривизну поверхности с тем же локальным направлением. Здесь мы начинаем подбираться к сути. Независимо от того, как ведет себя исходная CONS, мы получаем собственную дифференциальную характеристику поверхности, а именно ее нормальную кривизну, т.е. кривизну нормального сечения. Именно эту характеристику мы и желаем получить, когда говорим о кривизне поверхности вдоль направления.
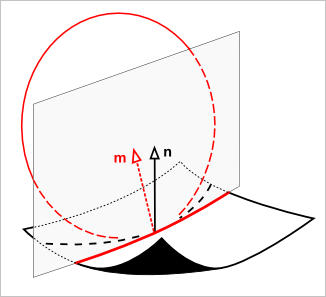
Учитывая, что локальная система координат поверхности зафиксирована и находится в нашем распоряжении, направление можно представить как направляющий тангенс (рис. 2).
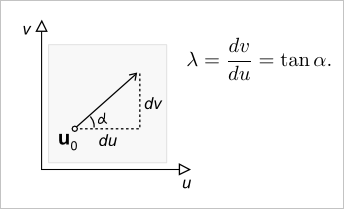
Рис. 2. Направление в параметрическом пространстве поверхности.
Теперь можно воспользоваться известной формулой и подсчитать нормальную кривизну по направлению лямбды:
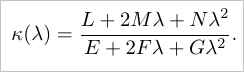
Заметим, что для вертикального направления в параметрическом пространстве тангенс окажется бесконечным, а в вычислительной практике это приведет к элементарному делению на ноль. В этом случае лямбду считать не нужно, так как достаточно заметить асимптотическое стремление нормальной кривизны к значению N / G (рис. 3).
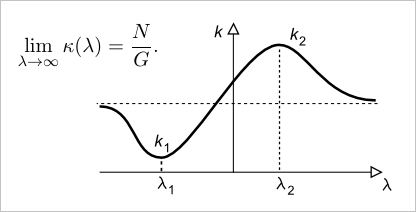
Рис. 3. Зависимость нормальной кривизны от направления в параметрическом пространстве. Минимум и максимум графика соответствуют главным кривизнам, которые нас здесь не интересуют (нам интересны не эти характерные точки функции, а значение функции в произвольной точке, включая бесконечность).
В качестве примера возьмем ребро и рассчитаем нормальную кривизну поверхности вдоль этого ребра. Будем считать, что направление задается касательным вектором для значения параметра t (аргумент функции).
//! This function is designed to evaluate curvature of the surface along the
//! the given edge. It takes the tangent direction of the edge's curve for
//! the passed parameter value and calculates the normal curvature at the
//! corresponding point on surface.
bool EvaluateAlongCurvature(const TopoDS_Face& face,
const TopoDS_Edge& edge,
const double t,
double& k)
{
// Get host geometries
double f, l;
Handle(Geom2d_Curve) c2d = BRep_Tool::CurveOnSurface(edge, face, f, l);
BRepAdaptor_Surface surf(face);
// Evaluate curve
gp_Pnt2d UV;
gp_Vec2d T;
c2d->D1(t, UV, T);
// Calculate differential properties
BRepLProp_SLProps Props(surf, UV.X(), UV.Y(), 2, 1e-7);
//
if ( !Props.IsCurvatureDefined() )
{
std::cout << "Error: curvature is not defined" << std::endl;
return false;
}
// Get differential properties
const gp_Vec Xu = Props.D1U();
const gp_Vec Xv = Props.D1V();
const gp_Vec Xuu = Props.D2U();
const gp_Vec Xuv = Props.DUV();
const gp_Vec Xvv = Props.D2V();
const gp_Vec n = Props.Normal();
// Coefficients of the FFF
const double E = Xu.Dot(Xu);
const double F = Xu.Dot(Xv);
const double G = Xv.Dot(Xv);
// Coefficients of the SFF
const double L = n.Dot(Xuu);
const double M = n.Dot(Xuv);
const double N = n.Dot(Xvv);
// Calculate curvature using the coefficients of both fundamental forms
if ( Abs( T.X() ) < 1.0e-5 )
k = N / G;
else
{
const double lambda = T.Y() / T.X();
k = (L + 2*M*lambda + N*lambda*lambda) / (E + 2*F*lambda + G*lambda*lambda);
}
return true;
}
Примеры использования данного кода показаны на рис. 4 и 5.
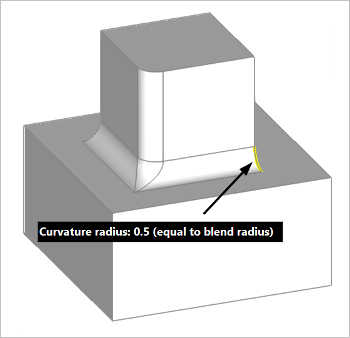
Рис. 4. Кривизна поверхности вдоль поперечного ребра скругления равна кривизне самого скругления.
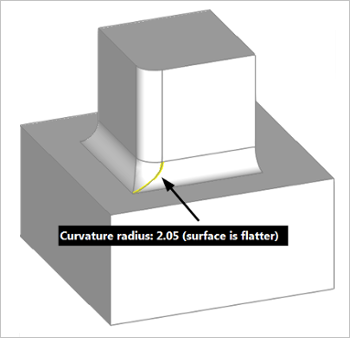
Рис. 5. Кривизна поверхности вдоль стыкующего ребра меньше кривизны вдоль ребра поперечного, так как стыкующее ребро более «пологое».
- [1] Farin G., Curves and Surfaces for CAGD. A Practical Guide, Morgan Kaufmann Publishers, 2001, 499p.
- [2] Рашевский П. К. Курс дифференциальной геометрии. - 3-е изд. - М.-Л.: ГИТТЛ, 1950. - 428 с.
Want to discuss this? Jump in to our forum.