Позиционирование развертки листовой модели

Вторник, 10 марта 2020 г. / Просмотров: 1938

Geometric modeling / Analysis Situs / Sheet metal / Прямое редактирование CAD / Тестирование и эксперимент

Распознавание и развертка листовых деталей — одно из приложений автоматического детектирования конструктивных элементов на базе аппарата AAG. В результате развертки формируется т.н. плоский шаблон — образ листового металла, из которого может быть получен чертеж для автоматизации производства. Эта же функциональность необходима для оценки стоимости изготовления листовой детали, поскольку нас интересуют габариты бланка, а также количество операций резания, сверления, сгибания и проч. Вообще, листовые металлы — это геометрически «удобный» класс моделей, допускающий полную алгоритмизацию вычислений без необходимости привлечения таких слабо детерминированных подходов, как, например, машинное обучение. Грубо говоря, используя наборы правил и эвристик, гораздо проще распознать листовую деталь, чем, например, деталь токарную или фрезерную.

Сегодня мы оставим в стороне сам принцип распознавания листовых деталей и рассмотрим подробнее небольшую, но интересную задачу о корректном позиционировании развертки. Допустим, что листовая деталь размещена в пространстве моделирования с некоторой трансформацией, соответствующей, например, ее реальному положению в сборке. В результате развертки плоский шаблон ляжет в пространстве сообразно положению исходной детали, то есть, вообще говоря, окажется невыровненным относительно проекционных видов. Это неудобно, поскольку произвольное расположение развертки затрудняет автоматическое создание чертежей. Желательно, поэтому, переместить развертку в одну из основных проекций (XOY, XOZ или YOZ) и выровнять ее таким образом, чтобы занимаемая ею площадь оказалась минимальной. Для корректного позиционирования следует выполнить две геометрические операции:

Переместить развертку в проекционную плоскость.
Довернуть ее так, чтобы она оказалась выровненной.

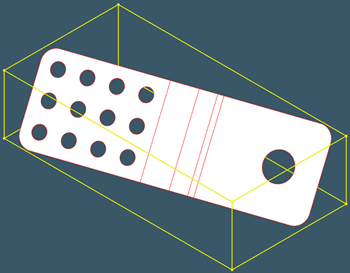Плоский шаблон после развертки произвольно ориентированной детали.

Первый шаг этой процедуры мы уже рассматривали. Он состоит в том, чтобы обеспечить совмещение координатных реперов развертки и целевой проекционной плоскости. Рассмотрим теперь второй этап, то есть «доворачивание» плоского шаблона до оптимального положения. Будем искать такой угол вращения $\phi$, который минимизирует площадь габаритного прямоугольника развертки в плоскости чертежа. Таким образом, мы имеем действительную функцию одного переменного $A(\phi)$, значением которой является площадь габаритного прямоугольника. Доворот шаблона есть задача $A \to \min$, причем угол $\phi$ задает вращение вокруг геометрического центра развертки.

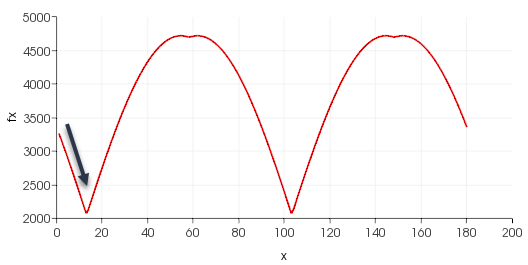Функция площади на интервале $phi in [0,180]$.

Для минимизации функции площади можно использовать один из алгоритмов локальной оптимизации. На практике хорошо себя зарекомендовал квазиньютоновский метод BFGS (Broyden-Fletcher-Goldfarb-Shanno), доступный в открытой библиотеке OpenCascade. Начинаем с задания функции площади — наследника базового класса math_MultipleVarFunctionWithGradient.

Мы используем BFGS для минимизации функции одной переменной, но следует иметь в виду, что тот же подход применим и для функций многих переменных.

Интерфейс класса-функции приведен ниже:

class DrawingAreaFunc : public math_MultipleVarFunctionWithGradient
{
public:
  
  //! Ctor accepting the shape representing a flat pattern.
  DrawingAreaFunc(const TopoDS_Shape&       shape,
                  const Handle(Geom_Plane)& refPlane);
  
public:
  
  //! Returns the number of variables.
  virtual int NbVariables() const
  {
    return 1;
  }
  
public:
  
  //! Evaluates this function.
  virtual bool
    Value(const math_Vector& X, double& F);
  
  //! Computes the gradient of a function.
  virtual bool
    Gradient(const math_Vector& X, math_Vector& G);
  
  //! Computes the function value together with its gradient.
  virtual bool
    Values(const math_Vector& X, double& F, math_Vector& G);
  
protected:
  
  TopoDS_Shape       m_shape;    //!< Flat pattern shape.
  Handle(Geom_Plane) m_refPlane; //!< Reference plane.
  gp_Pnt2d           m_center2d; //!< Center of the flat pattern in the reference plane.
  gp_Pnt             m_center;   //!< Center point in 3D.
  
};

Конструктор класса принимает развертку и плоскость, в которой будет производиться вращение. Заметим, что плоскость не должна выбираться из несущих граней самой развертки, т.к. в противном случае никакого вращения не получится: в собственной локальной системе координат плоский шаблон почти наверняка описан прямоугольником минимальной площади (за исключением случаев «странной» параметризации, когда ребра модели не направлены вдоль изопараметрических линий плоскости).

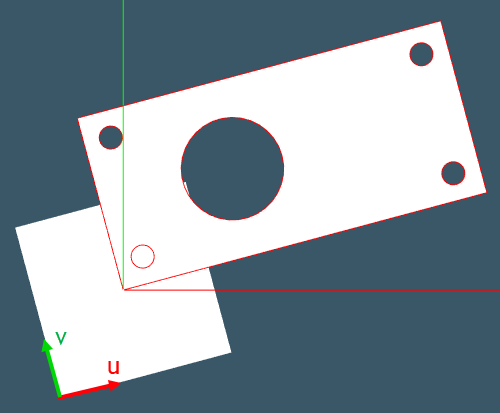К выбору плоскости отсчета: плоскость, параметризованная как показано на рисунке, не годится для оптимизации, т.к. развертка в ее локальной системе координат уже выровнена.

Роль конструктора состоит также в том, чтобы выбрать центр вращения модели.

DrawingAreaFunc::DrawingAreaFunc(const TopoDS_Shape&       shape,
                                 const Handle(Geom_Plane)& refPlane)
: math_MultipleVarFunctionWithGradient(), m_shape(shape), m_refPlane(refPlane)
{
  // Get the COG.
  GProp_GProps gprops;
  BRepGProp::SurfaceProperties(m_shape, gprops, 1e-3);
  m_center = gprops.CentreOfMass();
  
  // Compute the pinned center point.
  double cu, cv;
  GeomAPI_ProjectPointOnSurf(m_center, m_refPlane).Parameters(1, cu, cv);
  m_center2d.SetX(cu);
  m_center2d.SetY(cv);
}

Метод Value() вычисляет значение функции как площать двумерного габаритного прямоугольника. Аргумент функции — угол, заданный в радианах. Вращение вокруг центра есть произведение трех элементарных движений: перенос центра в начало координат (T1), вращение вокруг начала координат (RR) и возврат центра в исходное положение (T2). Габаритный прямоугольник формируется поточечно координатами $(u,v)$ вершин модели-развертки.

bool DrawingAreaFunc::Value(const math_Vector& X, double& F)
{
  if ( m_refPlane.IsNull() )
    return false;
  
  Bnd_Box2d aabb;
  
  // Move center point to the origin (T1), rotate (RR), then move back (T2).
  gp_Trsf2d T, T1, T2, RR;
  T1.SetTranslation( gp_Vec2d( m_center2d.XY() ).Reversed() );
  T2.SetTranslation( gp_Vec2d( m_center2d.XY() ) );
  RR.SetRotation( gp::Origin2d(), X(1) );
  T = T2*RR*T1;
  
  // Populate the two-dimensional AABB.
  for ( TopExp_Explorer vexp(m_shape, TopAbs_VERTEX); vexp.More(); vexp.Next() )
  {
    gp_Pnt P = BRep_Tool::Pnt( TopoDS::Vertex( vexp.Current() ) );
    
    // Get projection on the reference plane.
    double u, v;
    GeomAPI_ProjectPointOnSurf(P, m_refPlane).Parameters(1, u, v);
    //
    gp_Pnt2d Pproj(u, v);
    
    // Apply transformation.
    gp_Pnt2d PprojRot = Pproj.Transformed(T);
    
    // Add to the bounding box.
    aabb.Add(PprojRot);
  }
  
  double xMin, yMin, xMax, yMax;
  aabb.Get(xMin, yMin, xMax, yMax);
  
  // Compute area.
  F = Abs(xMax - xMin)*Abs(yMax - yMin);
  
  return true;
}

Метод BFGS — гладкий метод, поэтому целевая функция должна быть непрерывно дифференцируемой. В многомерном случае у целевой функции должен существовать градиент. Его мы вычисляем по центральной разностной формуле с фиксированным шагом $h = 1e^{-4}$:

bool DrawingAreaFunc::Gradient(const math_Vector& X, math_Vector& G)
{
  if ( m_refPlane.IsNull() )
    return false;
  
  const double h = 1.e-4;
  math_Vector  X_next = X + math_Vector(1, 1, h);
  math_Vector  X_prev = X - math_Vector(1, 1, h);
  
  double F_next, F_prev;
  this->Value(X_next, F_next);
  this->Value(X_prev, F_prev);
  
  const double dF = (F_next - F_prev) / (2*h);
  G = math_Vector(1, 1, dF);
  return true;
}

Также базовый класс требует реализации метода Values(), вычисляющего как значение функции, так и ее градиент. Реализация тривиальна:

bool DrawingAreaFunc::Values(const math_Vector& X,
                             double&            F,
                             math_Vector&       G)
{
  if ( !this->Value(X, F) )
    return false;
  
  return this->Gradient(X, G);
}

Запуск алгоритма оптимизации осуществляется следующим образом:

DrawingAreaFunc func(flatPattern, refPlane);
  
math_BFGS optimizer(1);
optimizer.Perform( func, math_Vector(1, 1, 0.) );
const math_Vector& resPhi = optimizer.Location();

Аргументами метода Perform() являются функция вычисления площади и начальное приближение, соответствующее значению $\phi = 0$, то есть развертке без доворота.

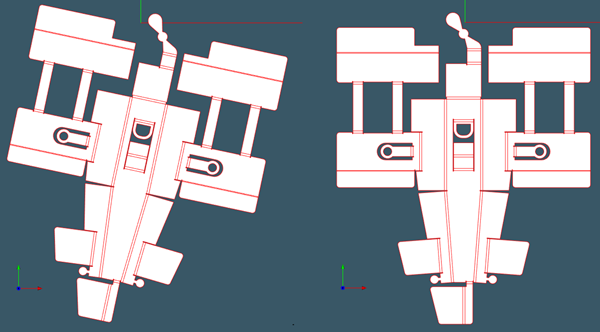Доворот плоского шаблона на 12 градусов за 4 итерации BFGS.

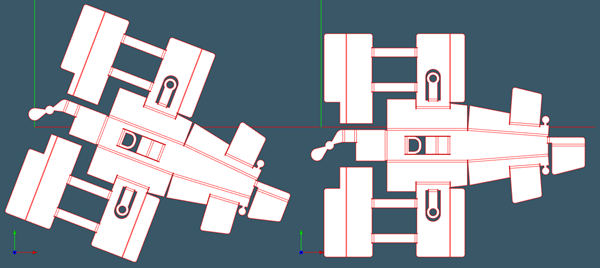Доворот плоского шаблона на 21 градус за 3 итерации BFGS.

Примеры выше демонстрируют удовлетворительное поведение алгоритма при сравнительно небольших отклонениях плоского шаблона от оптимального положения. Однако следует помнить, что BFGS — локальный метод, то есть с его помощью удается находить только локальные минимумы функции. Если начальное условие выбрано неудачно, развертка не займет желаемого положения в проекционном виде.

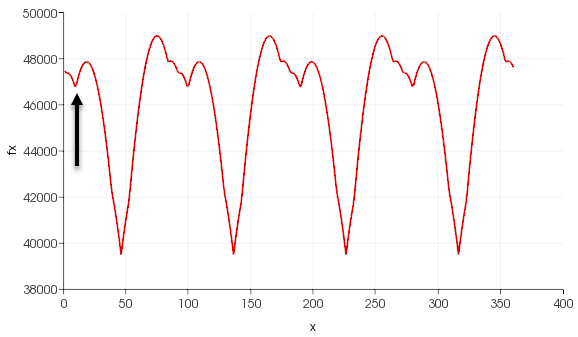Функция площади со множеством локальных минимумов — «ловушек» BFGS.

Для исправления этой ситуации требуется предварить локальный поиск глобальным, таким, например, как PSO. Не следует также забывать о том, что положение плоского шаблона выбирается в два этапа, о чем было сказано в начале этой заметки (совмещение координатных реперов и собственно оптимизация). Выполнение первого этапа может дать достаточно хорошее начальное приближение для успешного поиска оптимума.

Want to discuss this? Jump in to our forum.