Штрафная схема PSO для вычисления расстояния между кривыми
Постановка задачи
Допустим, что заданы две пространственные параметрические кривые $c(t)$ и $r(p)$. Требуется эти кривые пересечь, либо найти минимальное расстояние между ними. Заметим, что кривые, вообще говоря, параметризованы по-разному, следовательно, искомое решение (пересечение, либо пара точек минимального расстояния) описывается двумя компонентами $(t, p)$ параметров этих кривых. Оптимальных точек может быть несколько, и найти обычно нужно все (рис. 1). Заметим также, что в геометрических ядрах принято работать со специальными видами параметрической геометрии, выделяя из общего класса прямые, конические сечения, кривые Безье и т.д. Естественно, что в специальных случаях задача упрощается, однако мы рассмотрим общую ее постановку.
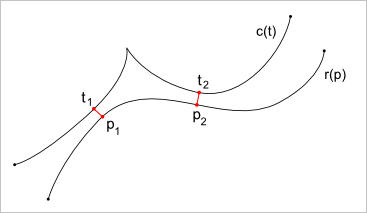
Рис. 1. Две оптимальные точки.
Итак, решение задачи о минимальном расстоянии есть точка в двумерном параметрическом пространстве — пространстве решений. В этом пространстве решений, вообще говоря, необходимо выделить некоторую область $D$, на которой заданы обе исходные кривые. Понятно, что речь идет о прямоугольнике (рис. 2), из границ которого выходить нельзя, так как вне области $D$ кривые $c(t)$ и $r(p)$ не существуют.
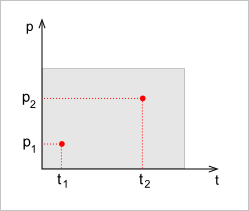
Рис. 2. Две оптимальные точки в пространстве решений.
Для каждой точки $(t, p) \in D$ можно подсчитать значение $\rho(t, p) = \left( c(t) - r(p) \right)^2$, т.е. квадратичное расстояние между точками кривых (здесь мы пользуемся нормой $\lVert c(t) - r(p) \rVert$, определенной, как корень из скалярного квадрата функции). Ясно, что решение задачи доставляет минимум функции $\rho$, т.е. ставится задача оптимизации. Размерность задачи всего-лишь 2 (у нас два независимых параметра $t$ и $p$), поэтому какой бы численный метод мы ни использовали, решение всегда можно проверить при помощи «грубой силы», т.е. «сэмплируя» функцию $\rho$ на некоторой сетке по области $D$ (мы проделаем это ниже).
Методы оптимизации — обширная и динамично развивающаяся область знаний, которую можно отнести к синтетической науке кибернетике. Оптимизация широко применяется в различных прикладных областях, где требуется из серии возможных решений выбрать некоторое наилучшее. Эти задачи не просто сложны. По словам Нестерова [1], «главное, что следует знать каждому, работающему с оптимизационными моделями, — это то, что задачи оптимизации, вообще говоря, численно неразрешимы». Это означает, что универсального рецепта в оптимизации нет. В каждой ситуации необходимо четко знать, к какому классу задач относится решаемая, и какие методы могут быть правомерно помещены в обойму вычислителя. Так, если задача негладкая (т.е. производная функции $\rho$ терпит разрыв), то методы, использующие градиент должны быть исключены. Если задача невыпуклая, то поисковая оптимизация становится еще сложнее, так как на каждом шаге мы не можем быть уверены, что позади выбранного направления поиска не осталось возможно упущенной оптимальной точки. Существует множество нюансов, связанных со скоростью сходимости и оценкой шага поискового метода. Кроме того, методы оптимизации существенно различны для линейных и нелинейных задач. Поэтому, прежде чем мы сможем выбрать подходящий метод, следует выяснить, к какому классу относится задача $\rho \to min$.
Рассмотрим две кривые, заведомо полагая, что гладкость любой из них не выше $C^0$ (рис. 3). В случае нормированных базисных сплайнов мы имеем область определения в виде единичного квадрата $D = \Pi = [0,1] \times [0,1]$.
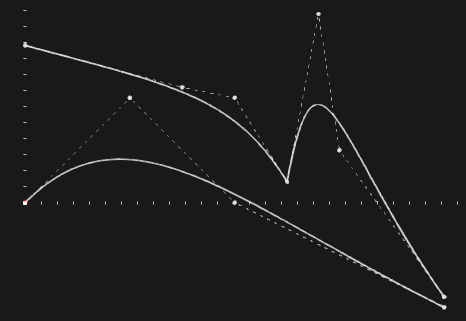
Рис. 3. Две плоские B-кривые степени 3. Верхняя кривая негладкая.
Изучим поведение функции $\rho$ путем тривиального «сэмплирования» квадрата $\Pi$. Для этого с некоторым шагом осуществим перебор точек $(t,p)$ и подсчитаем для каждой пары значение целевой функции. Условимся значение функции отображать цветом на диаграме уровня (рис. 4).
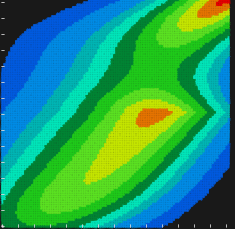
Рис. 4. Диаграмма уровня целевой функции, полученная путем «сэмплирования» области $\Pi$.
Из диаграммы очевидно (впрочем, это было ясно и без нее), что целевая функция оказывается многоэкстремальной и негладкой (обратите внимание на клиновидный фронт в правой части диаграммы). Более того, вне области $\Pi$ целевая функция не определена, следовательно, метод поисковой оптимизации не должен «вываливаться» за пределы этого квадрата. Аналогичные диаграммы удобно строить для задач минимальных размерностей (двумерных и трехмерных). Здесь мы не только видим, какова природа целевой функции, но для выбранного метода оптимизации мы можем дополнительно проследить траекторию поиска и сделать некоторые выводы о его скорости сходимости. В нашем случае речь должна идти о негладкой многоэкстремальной оптимизации с простыми ограничениями на границы области $\Pi$. Популярным методом такой оптимизации является Рой Частиц (Particle Swarm Optimization).
Рой Частиц (Particle Swarm Optimization)
Введение
Рой частиц (PSO — Particle Swarm Optimization) представляет собой простой и прозрачный метод поисковой оптимизации. В методах оптимизации принято говорить о так называемых «испытаниях», которые состоят в получении некоторой информации о целевой функции на каждой итерации. Например, в случае гладкой оптимизации испытание может состоять в вычислении значения функции, ее градиента и гессиана. Если вычисляется только значение функции, то мы не знаем, в каком направлении она убывает (нет градиента), поэтому часто используется некоторая эвристика. PSO — это популярный эвристический способ перебора, эффективность которого достигается за счет хитро организованной схемы испытаний. Метафорически выражаясь, ход испытаний эмулирует движение пчелиного роя, отчасти стохастическое. Частицы (пчелы, агенты, etc.) пролетают в области $D$, снимая информацию о том, где целевая функция «лучше» или «хуже». Каждая частица описывает некоторую траекторию, которая, вообще говоря, зависит как от личных испытаний частицы, так и от совокупных результатов всего роя или его подмножества. Эти два фактора называют когнитивным и социальным поисковыми параметрами (детерминантами). Согласно [2], можно утверждать, что чем выше когнитивный детерминант пчелы (он отвечает за «ностальгию», то есть стремление частицы вернуться в ту область, где значение целевой функции на ее личных испытаниях было наилучшим), тем медленнее сходимость. С другой стороны, чем больше социальный детерминант, тем выше сходимость, но тем больше и вероятность угодить в «ловушку» локального минимума, т.е. упустить из вида одно или несколько оптимальных решений, проведя весь рой мимо них. Социальный детерминант пчелы определяется теми социальными связями, которые мы для нее установим. Так, если каждая пчела имеет социальные связи со всеми остальными, то она движется сообразно целому рою, из которого не выделяются независимые группы. В оригинальной работе [3] указывается, что лучше всего иметь оба детерминанта сбалансированными. Сказать что-то более определенное можно лишь экспериментируя над конкретным классом задач.
Эмулирование роя частиц для нужд оптимизации было подсказано поведением птиц. Стоит бросить где-нибудь корм, как через некоторое время вы обнаружите стайку птиц, слетающихся к нему, причем заведомо нельзя предположить, что птицы знали, где именно этот корм находится. Появление одной птицы вызывает социальную реакцию у сородичей, в результате чего сразу несколько особей совершают посадку в одном месте. Заметим здесь, что метафорическая красота метода не должна приводить читателя в благоговейный трепет. Достаточно вспомнить, что классический PSO не использует в испытаниях никакую другую информацию о целевой функции, кроме ее значений. Следовательно, это не более чем изящный способ перебора, т.е. метод не самый быстрый и притом далеко не самый точный. Но об этом мы подробнее поговорим ниже.
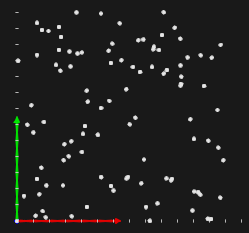
Рис. 5. Начальное стохастическое распределение 100 агентов в области $\Pi$.
Начальное распределение агентов при отсутствии какой-либо априорной информации о виде целевой функции удобно выбирать равномерным (рис. 5). В идеале используемый генератор псевдослучайных чисел (RNG, Random Number Generator) должен всегда выдавать одно и то же распределение для данного seed-числа. Если это не так, то чисто стохастическое поведение алгоритма существенно усложнит подход к его автоматизированному тестированию. Кроме того, RNG должен быть по возможности очень быстрым. Отличный обзор по теме сделал Ян Буллард, представивший алгоритм, код которого с небольшими изменениями приведен ниже.
//! RNG based on code presented by Ian C. Bullard (more
//! accurate than standard C rand() and at least 10 times
//! faster).
class BullardRNG
{
public:
inline BullardRNG(const unsigned seed = 1)
{
this->Initialize(seed);
}
inline void Initialize(const unsigned seed)
{
m_iHi = seed;
m_iLo = seed ^ 0x49616E42;
}
inline unsigned RandInt()
{
static const int shift = sizeof(int) / 2;
m_iHi = (m_iHi >> shift) + (m_iHi << shift);
m_iHi += m_iLo;
m_iLo += m_iHi;
return m_iHi;
}
inline double RandDouble()
{
return RandInt() / (double) (0xFFFFFFFF);
}
protected:
unsigned m_iLo, m_iHi;
};
Следует заметить, что число агентов обычно выбирается небольшим (50-100). Если плотность точек высока (рис. 6), то PSO фактически вырождается в обыкновенный перебор, производительность которого на практике редко бывает приемлема. Особенно это относится к случаю многомерной оптимизации. Вычислительные эксперименты, проводимые над пространственными параметрическими кривыми показали, однако, что для небольших популяций частиц (до 100 агентов) метод выдает плохие результаты. Это вынуждает нас увеличивать количество агентов до тех пор, пока результат не станет удовлетворительным. Кроме того, имеет смысл «насильно» добавить дополнительных агентов вдоль границ области, так как в задачах нахождения минимального расстояния часто экстремум достигается на границах.
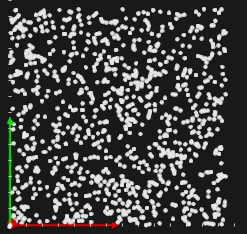
Рис. 6. Начальное стохастическое распределение 1000 агентов в области $\Pi$.
На первом этапе каждый агент проводит испытание с целью получить глобально (среди всех агентов) наилучший результат (рис. 7). Здесь происходит обыкновенный перебор значений.
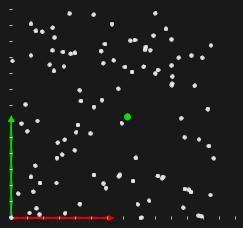
Рис. 7. Зеленым маркером отмечено наилучшее начальное приближение.
Динамика роя частиц подчиняется двум основным уравнениям. Скорость частицы вычисляется по следующей формуле:
$v := mv + (p_{best}^{individual} - p) \mu_{cognition} \mu_{random} + (p_{best}^{social} - p) \nu_{social} \nu_{random}$
Имея предыдущее положение частицы и скорость, мы вычисляем ее новое положение следующим тривиальным способом:
$p := p + v$
Мы видим, что скорость каждой частицы складывается из трех компонент:
- Скорость на предыдущем шаге с коэффициентом инерции $m$.
- Когнитивная составляющая, направляющая частицу в зону наилучшего личного результата $p_{best}^{individual}$.
- Социальная составляющая, направляющая частицу в зону наилучшего результата целого роя $p_{best}^{social}$.
Параметры $\mu_{cognition}$ и $\nu_{social}$ выбираются из соображений сходимости и не изменяются в ходе вычислений. Параметры $\mu_{random}$ и $\nu_{random}$ есть псевдослучайные числа из интервала $(0, 1)$. Они вычисляются заново для каждой частицы на каждой итерации, поэтому производительность используемого RNG должна быть хорошей. В простейшем случае рой частиц ведет себя как целое, то есть, если хотя бы одна частица в ходе испытаний смогла улучшить коллективный результат, то все прочие частицы роя устремляются (в силу социального детерминанта) в эту зону. Простейшим критерием останова может служить проверка того, что все частицы имеют скорости близкие к нулю.
Нетрудно видеть, что алгоритм подобного рода способен дать лишь одно решение. Никакая частица на практике не может осесть в «чашке» локального минимума, если какая-то другая частица нашла более оптимальное значение функции. Даже если несколько экстремумов являются глобально оптимальными, весь рой будет направлен в единственную точку $p_{best}^{social}$, т.е. множественность решений здесь исключена. Для решаемой нами задачи это ограничение очень существенно, так как кривые могут приближаться друг к другу сразу в нескольких местах. Следовательно, метод PSO нуждается в модификации.
Мультимодальные функции
Выделим следующие виды целевых функций:
- Унимодальная функция — один минимум (глобальный).
- Мультимодальная функция с одним глобальным минимумом и множеством локальных минимумов.
- Мультимодальная функция со множеством локальных минимумов, среди которых есть несколько глобально оптимальных.
Понятно, что в задаче о нахождении ближайших точек двух кривых мы имеем дело с третьим случаем. По существу, здесь мы должны говорить о существовании нескольких глобальных минимумов (в нестрогом смысле). Далее заметим, что в вычислительной практике нам непозволительно отсеивать те минимумы, в которых значение целевой функции всего-лишь немного хуже глобально оптимального. Всегда нужно иметь в виду наличие ошибок округления, а также погрешности самой задачи, которые могли превратить глобально оптимальное решение в локально оптимальное. В инженерной практике для мультимодальных функций часто нужно уметь находить все локальные (глобальные) минимумы. В дальнейшем те из них, что не представляют интереса для вычислителя, могут быть отброшены, исходя из каких-то прикладных соображений.
В мультимодальной оптимизации посредством PSO можно выделить два существенно различных подхода. Первый состоит в разделении всего роя на подмножества (маленькие рои), каждое из которых имеет собственный наилучший коллективный результат. В силу независимости этих множеств мы можем надеяться, что частицы «осядут» в разных «чашечках» локально оптимальных решений. Здесь, однако, надо гарантировать, что маленькие рои частиц не разбросаны по области поиска, т.е. все агенты сосредоточены рядом друг с другом. В противном случае некоторый агент может вторгнуться в область другого, нежелательного для нас минимума, уведя за собой весь рой. Можно поступить иначе. Другой способ мультимодальной оптимизации состоит в том, что PSO используется несколько раз (последовательно или параллельно) до тех пор, пока не будут найдены все решения. При этом с каждым новым запуском PSO целевая функция изменяется таким образом, чтобы она была лишена локальных минимумов, найденных на предыдущих этапах. В результате мы шаг за шагом находим все экстремумы на обновленной целевой функции. Так или иначе, нашей целью является получение не одной, а всех оптимальных точек, что особенно востребованно в системах автоматизированного принятия решений.
Модификация целевой функции для последовательного исключения найденных ранее экстремумов — способ обманчиво простой. Его суть состоит в добавлении к исходной функции некоторого «всплеска» $s(t, p; t_0, p_0)$, который должен «приподнять» ранее полученный минимум, естественным образом исключив его из последующих результатов:
$\rho(t, p) := \rho(t, p) + s(t, p; t_0, p_0)$
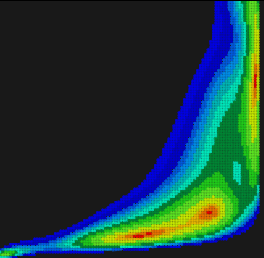
Рис. 8. Исходная функция.
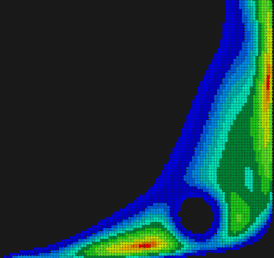
Рис. 9. Модифицированная функция после нахождения первого экстремума.
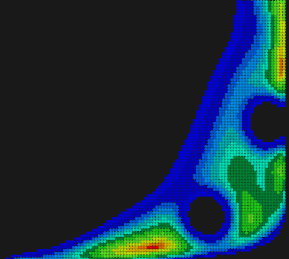
Рис. 10. Модифицированная функция после нахождения второго экстремума.
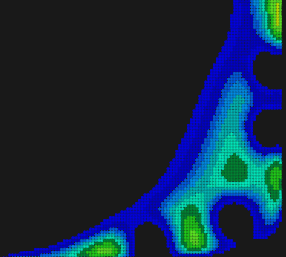
Рис. 11. Модифицированная функция после нескольких итераций.
На диаграммах уровня 8-11 модификация целевой функции выглядит как прокалывание дырок. Понятно, что для успешного применения такого подхода экстремумы должны быть изолированными. Кроме того, заранее непросто настроить разрешающую способность подобного метода, то есть указать радиус «дырки», которую следует «проколоть». Этот радиус не должен быть слишком мал, чтобы его хватило на поглощение преобладающей части «чашки» минимума. Но он также не должен быть и слишком велик, чтобы не пострадали соседние изолированные минимумы. Процесс прокалывания дырок следует остановить, когда все вновь получаемые решения начнут становиться хуже допустимых в смысле значения целевой функции. В задаче нахождения минимальных расстояний дальнейший поиск не имеет смысла, если следующая найденная дистанция существенно превосходит предыдущую. Данное обстоятельство усугубляет дело, так как нам требуется одна заведомо избыточная итерация всего-лишь затем, чтобы вовремя остановиться. Функция для «прокалывания дырки» назвается штрафной (penalty function). Она должна иметь локальный носитель и быть вычислительно эффективной. Удобным, но не лучшим способом задания такой функции является произведение базисных сплайнов, формирующих своеобразный всплеск целевой функции (рис. 12).
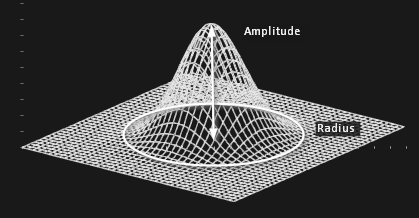
Рис. 12. Штрафная функция в виде произведения двух B-сплайнов.
В целом излагаемый подход идеологически близок к работе [6], где вместо сплайнового всплеска используется гауссова форма штрафной функции. Кроме того, вместо последовательного запуска PSO в работе [6] используется параллельный, что вполне естественно для данного метода в силу слабой зависимости данных. При этом на каждой итерации все действующие популяции обмениваются своими глобально наилучшими результатами с тем, чтобы правильно наложить штраф в популяциях-компаньонах. Излагаемый метод хорош тем, что он очень прост в реализации и по сути представляет собой не модификацию PSO, а вычислительную схему надстоящую PSO. С другой стороны, как мы видели, есть проблема, связанная с адекватным выбором радиуса дырки, а также с критерием останова.
Повышаем точность
PSO — не особенно точный метод. На практике им можно удовлетвориться лишь в том случае, если погрешность самой задачи довольно высока (например, при наличии серьезного «шума» в исходных данных). Но в области САПР, а особенно в направлении CAGD (Computer-Aided Geometric Design), имеющем дело с задачами геометрического моделирования, как правило, точность PSO оказывается неудовлетворительной. Так, нахождение расстояний между двумя кривыми — дело существенно тонкое, где обычно требуется выдерживать очень малую ошибку (порядка 1e-9 или 1e-11). Это, однако, не означает, что от PSO следует отказаться. Напротив, PSO дает отличный способ приближения к экстремумам, то есть его результаты могут использоваться как начальные условия для вторичного локального поиска.
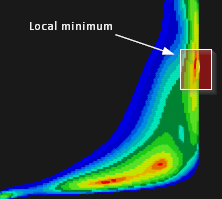
Рис. 13. Локальный минимум подлежащий уточнению.

Рис. 14. Траектория уточнения результата PSO (вид издалека).
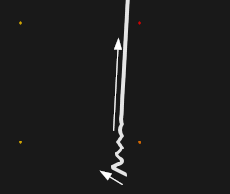
Рис. 15. Траектория уточнения результата PSO (вид вблизи).
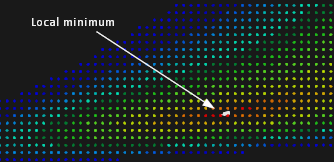
Рис. 16. Уточнение результата PSO (вид издалека).
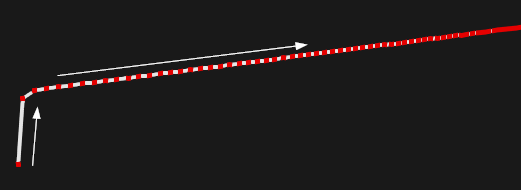
Рис. 17. Уточнение результата PSO (вид вблизи). Красным показаны точки, в которых проводились испытания.
Для уточнения результатов PSO мы пользовались простейшим методом градиентного спуска. Известно, что это далеко не самый эффективный метод локальной оптимизации (см., например, [4]), так как он может делать много лишних шагов, не приближаясь к минимуму. Это особенно актуально для овражных функций, что для нашей задачи означает ситуацию, когда кривые выходят на касание. На рис. 16-17 показан портрет сходимости для неовражного случая. Здесь использовался метод градиентного спуска с фиксированным шагом. Последнее обстоятельство не должно вводить в заблуждение. Фиксированный шаг не означает, что поиск осуществляется с равномерным смещением вдоль антиградиента. Действительный шаг испытаний зависит еще и от модуля самого антиградиента, который постоянно уменьшается, что мы и видим на рис. 17.
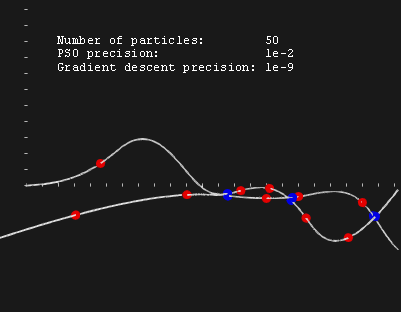
Рис. 18. Уточнение результатов PSO.
На рис. 18 показан результат решения задачи методом PSO с модификацией целевой функции (красные шарики), а также результаты уточнения методом градиентного спуска (синие шарики). Мы видим, что модифицированный PSO нанизывает бусины начальных приближений в грубой окрестности реальных решений. Затем локальный поиск корректирует положения бусин, доводя результат до требуемой точности. Мы могли бы увеличить точность самого PSO, чтобы избежать необходимости локального поиска. Однако это было бы неразумное решение, так как локальные методы в целом более эффективны. Они учитывают дифференциальные свойства функции (если она гладкая) и требуют меньшего количества шагов. Так, в приведенном случае было бы правильнее использовать локальную оптимизацию методом Ньютона (если функция гладкая до второго порядка), либо BFGS (если есть гладкость только до первого порядка) вместо метода градиентного спуска. Последний мы выбрали только из-за исключительной простоты его реализации.
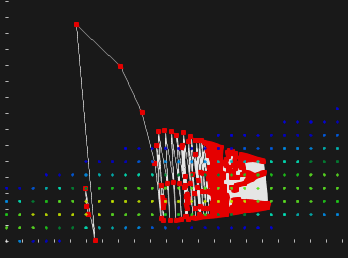
Рис. 19. Расходящийся метод градиентного спуска на овражной функции с неудачно подобранным шаговым множителем.
Постоянный шаговый множитель для метода градиентного спуска, как правило, плохо работает на задачах общего вида. Если он выбран слишком малым, то для сходимости с требуемой точностью уйдут десятки тысяч итераций. Если же выбрать шаговый множитель слишком большим, то мы рискуем и вовсе лишиться сходимости (рис. 19). Порог этого качественного изменения зависит от конкретной функции, а точнее от рельефа конкретного минимума, в окрестности которого осуществляется поиск. На рис. 20 показана типичная ситуация с расходящимся методом локальной оптимизации. Мы видим, что три экстремума (справа) между кривыми были найдены точно, тогда как результат четвертого локального поиска (экстремум слева) оказался даже хуже начального приближения, полученного при помощи PSO. В данном случае метод градиентного спуска исчерпал лимит итераций, так и не найдя решение.
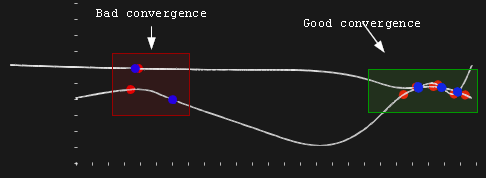
Рис. 20. Неудачно подобранный шаговый множитель дает неправильный конечный результат.
На рис. 21 показан результат для шагового множителя уменьшенного в 10 раз. При этом количество итераций, затраченных для достижения точности 1e-9 превысило 10 тысяч! Так, ценой радикального повышения интенсивности счета мы улучшаем надежность алгоритма. Это, однако, не гарантирует нас от ошибок, т.к. всегда можно изобрести еще более овражную функцию, где выбранный множитель перестанет работать.
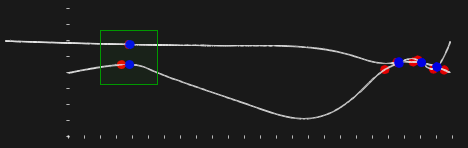
Рис. 21. «Исправленный» метод работает очень медленно.
Для преодоления этой существенной трудности можно использовать адаптивный шаговый множитель. Идея заключается в том, что величина множителя подбирается на каждой итерации, исходя из локального поведения целевой функции. Понятно, что адаптивный метод увеличивает вес одной итерации, но само количество итераций при этом радикально уменьшается, что дает суммарный выигрыш в производительности. Более того, адаптивная стратегия позволяет вычислителю избавиться от подбора «оптимального» и пригодного на все случаи жизни «волшебного числа», которым для рис. 21 стало значение 1e-4. Относительно «дешевой» адаптивной стратегией является правило Армихо (Armijo rule) [4]. Это правило требует однократного вычисления градиента, после чего небольшое количество итераций затрачивается на подбор подходящего шага. Каждая из таких вложенных итераций, в свою очередь, требует вычисления значения целевой функции без градиента, то есть проводимые испытания относительно легковесны. Следует заметить, что адаптивный выбор шага — это необходимая мера, которая улучшает качество градиентного поиска, но никаких чудес не совершает. Сам по себе метод очень медленный, поэтому пользоваться им на практике не всегда допустимо. Но если уж решили пользоваться — не забудьте про адаптивный шаг!
Понятно, что метод градиентного спуска, как и любой другой метод гладкой оптимизации, не подойдет, если исходные функции не являются гладкими (рис. 1, 3). В этом случае желательно использовать локальные негладкие методы, например, метод Пауэлла [5]. Негладкий случай легко распознать, если речь идет о B-кривых. Действительно, гладкость здесь может нарушаться только в узловых точках, причем информация о гладкости выводится из порядка B-сплайна и кратности соответствующего узла. Более того, негладкий случай в CAGD сам по себе патологичен. Многие библиотеки геометрического моделирования и вовсе декларируют, что их алгоритмы не застрахованы от ошибок на геометрии качества $C^0$. Обычно такие негладкие стыки избегаются расщеплением кривой и образованием двух (уже вполне гладких) ребер.
Вычислительная схема
Итак, для решения задачи о наименьшем расстоянии между двумя кривыми мы примем следующую вычислительную схему:
- При помощи глобального метода PSO для мультимодальных функций находим все решения задачи. Заметим, что точность решения здесь оказывается неудовлетворительной.
- При помощи локального метода уточняем решение задачи. Заметим здесь, что при отсутствии производных мы должны пользоваться негладкими методами, такими как метод Пауэлла (Powell). Если доступны первые производные, то есть возможность использовать градиентные методы, в частности, метод скорейшего спуска, метод сопряженных градиентов или BFGS. Если доступны вторые производные (а значит и гессиан), то лучше всего использовать метод Ньютона.
- На заключительном этапе осуществляем выбраковку тех решений, что не дают минимального расстояния.
Решение в Open CASCADE Technology
Теория и некоторые результаты, изложенные выше, не оставляют сомнений в том, что даже такая, казалось бы, простая задача, как вычисление расстояния между кривыми, на деле оказывается не совсем тривиальной. Это связано, конечно, с тем, что в общем случае мы вынуждены решать задачу многоэкстремальной негладкой оптимизации, привлекая целую линейку итерационных методов. Ясно, что в серьезных математических пакетах эта линейка еще шире, так как решение задачи можно провести быстрее, проще, а иногда и точнее, если учитывать конкретный тип кривых, а также порядок их гладкости. Все это мы оставили без рассмотрения, лишь упомянув мимоходом о том, что в некоторых случаях вместо метода градиентного спуска можно использовать метод Пауэлла, BFGS или даже итерации Ньютона. Сам по себе PSO нельзя считать state-of-the-art алгоритмом глобальной оптимизации при всем его богатом философском подтексте. Действительно, точность метода невысока, а подбор его параметров требует пристального внимания со стороны вычислителя. Так как задача о вычислении расстояния между кривыми обычно не является самоценной, а привлекается лишь как этап какой-то более сложной вычислительной схемы, мы не можем здесь допустить низкую производительность. Возникает вопрос о том, какая процедура вычисления расстояний между кривыми оказывается наиболее точной, быстрой и надежной. Мы оставляем этот вопрос открытым.
Обратимся теперь к единственной общедоступной библиотеке геометрического моделирования Open CASCADE Technology (OCCT) и посмотрим, каким образом наша задача решается там. Все, что касается расстояний между геометрическими объектами в OCCT реализовано в пакете Extrema. Здесь находятся методы вычисления расстояний между двумя кривыми, двумя поверхностями, кривой и поверхностью, кривой и точкой, точкой и поверхностью. Пакет Extrema — это один из основых модулей той части библиотеки OCCT, которая обычно называется «математическим обеспечением» геометрического моделирования. Помимо Extrema туда же можно отнести функции интерполяции и аппроксимации, а также всю линейную алгебру, которая полностью реализована на стороне OCCT (в отличие от, например, библиотеки ACIS, где, насколько мы можем судить из открытых источников, применяется библиотека Eigen).
Итак, раз Extrema — это пакет математического обеспечения, то должна существовать его высокоуровневая обвязка. Она находится в пакете GeomAPI, а интересующая нас функция реализована инструментальным классом GeomAPI_ExtremaCurveCurve. В отличие от той же библиотеки ACIS, где API представлен в виде глобальных функций, в OCCT используются не функции, а классы. То есть, чтобы решить поставленную задачу, нужно завести экземпляр класса GeomAPI_ExtremaCurveCurve и проинициализировать его исходными кривыми (расчет произойдет автоматически сразу после инициализации). Отметим здесь, что открытый исходный код библиотеки позволяет нам использовать не только API, но и любой низкоуровневый инструментальный класс, что нередко просто невозможно в коммерческих библиотеках. Листинг кода для вычисления минимального расстояния между кривыми приведен ниже.
//-------------------------------------------------------
// NOTICE: the following code is relevant for OCCT 6.9.1
//-------------------------------------------------------
// Prepare domain bounds
double U1f, U1l, U2f, U2l;
U1f = curve1->FirstParameter();
U1l = curve1->LastParameter();
U2f = curve2->FirstParameter();
U2l = curve2->LastParameter();
// Run extrema
GeomAPI_ExtremaCurveCurve Ex(curve1, curve2, U1f, U1l, U2f, U2l);
gp_Pnt P1, P2;
if ( Ex.TotalNearestPoints(P1, P2) )
{
const double uncertainty = P1.Distance(P2);
// In this example we are interested only in those curves
// which are close enough to each other
if ( uncertainty < precision )
{
// Get result as two parameter values on the input curves
Quantity_Parameter W1, W2;
Ex.TotalLowerDistanceParameters(W1, W2);
// Get result as average point in between
gp_Pnt P = 0.5*( P1.XYZ() + P2.XYZ() );
}
}
Класс GeomAPI_ExtremaCurveCurve сам по себе не делает почти никакой полезной работы. Сама вычислительная схема реализована в методе Perform() класса Extrema_ExtCC (CC означает Curve-Curve). Заглянув туда, мы быстро обнаружим, что OCCT рассматривает специальные случаи для различных типов кривых. Как было отмечено выше, это делается с целью повышения эффективности расчета. В общем случае применяется алгоритм Extrema_GenExtCC, не делающий никаких предположений относительно вида кривых. Алгоритм опирается на метод глобальной оптимизации, реализованный в пакете math_GlobOptMin. В отличие от подхода, изложенного выше, здесь используется не PSO, а другой метод, известный как метод Евтушенко.
Заключение
Мы рассмотрели один из самых простых методов расчета расстояний между двумя кривыми. Конечно, существуют куда более эффективные решения, реализованные в индустриальных геометрических ядрах, например, в Open CASCADE Technology. Но последнее слово здесь еще не сказано. Нетрудно заметить, например, что предложенный выше метод работает медленно на сильно овражных функциях, которые появляются всякий раз, когда кривые проходят почти параллельно или касаются друг друга. В таких случаях вместо изолированного решения бывает полезно вернуть целую зону соприкосновения, указав параметрические границы такой «сингулярности». Очевидно, что метод штрафа, описанный выше, не годится для такого расширения. Вообще же вопрос о том, какая оптимизационная схема является для нашей задачи наилучшей, остается открытым. Практически любая научная статья, посвященная той или иной модификации PSO, завершается сравнением предлагаемого ею метода с другими. Обычно это делается на наборе функций специального вида таких, например, как функция Растригина. С другой стороны, в области САПР нас интересуют прежде всего овражные случаи, тогда как общее число экстремумов, как правило, оказывается небольшим (откуда функция подобная растригиновской может взяться в нормальной геометрической модели?). Анализ оптимизационных схем в приложениях к геометрическому моделированию все еще ждет своих исследователей.
- [1] Ю.Е. Нестеров, Методы выпуклой оптимизации
- [2] M. Reyes-Sierra, C. Coello, Multi-Objective Particle Swarm Optimizers: A Survey of the State-of-the-Art
- [3] J. Kennedy, R. Eberhart, Particle Swarm Optimization, 1995
- [4] С.Ю. Городецкий, Лабораторный практикум по методам локальной оптимизации в программной системе LocOpt, 2007
- [5] M.J.D. Powell, An efficient method for finding the minimum of a function of several variables without calculating derivatives
- [6] E. Zafarani-Moattar, H. Haj-Seyed-Javadi, Parallel Reverse Niching PSO for Multimodal Optimization, International Conference on Machine Learning, 2014
2017-07-20 в 13:57:27
Спасибо за статьи. Информативная. Разбираю метод Евтушенко. Ну и описанный заодно погляжу :)
2017-07-20 в 14:05:46
Глядите сразу реализацию в OpenCascade, там метод индустриализован. Описанное в заметке — это микропрототип, которому еще зреть и зреть.