Зачем нужен AAG
"Feature models can be regarded as an extension to solid modeling techniques. They are designed to overcome some of the deficiencies of solid modeling, and they provide increased functionality for various applications in CAD and CAM (J. Shah, M. Mantyla. Parametric and Feature-based CAD/CAM).
На практике приходится сталкиваться с недопониманием, зачем де нужен атрибутированный граф смежности (Attributed Adjacency Graph = AAG), если исходная граничная модель и так содержит все необходимые данные. Чтобы расставить акценты правильно, отметим сразу, что сам по себе AAG не является чем-то качественно отличным от привычных структур B-Rep. Любая задача, решаемая с привлечением механизма AAG, может быть решена и без него. Вопрос лишь в том, какой ценой. Осмелимся утверждать, что будучи реализованными без привлечения графа смежности, некоторые алгоритмы рискуют превратиться в спагетти-коды, начисто лишенные сквозной руководящей идеи и потому совершенно безобразные. Этого мало? Едва ли.
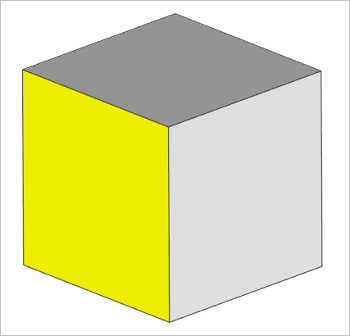
Кубик с выделенной гранью (показана желтым цветом).
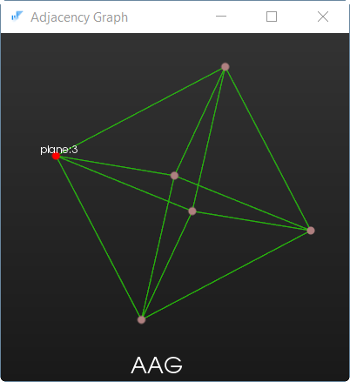
Граф смежности граней кубика. Выделенная грань отмечена в графе красным цветом.
Остановимся чуть подробнее на классе задач, решаемых при помощи AAG. В первую очередь, это распознавание конструктивных элементов (фичеров) из «немой» геометрии. В действительности, AAG появился именно как средство решения задачи распознавания, которая, в свою очередь, возникла из нужды планирования техпроцесса. Благодаря графу смежности, содержащему данные о выпуклости и вогнутости ребер, удается различить некоторые базовые конструктивные элементы, например, цилиндрические отверстия и карманы. Это классика. Помимо этого, граф смежности является просто удобной структурой хранения данных, позволяющей акцентировать отношение смежности, лишь неявно задаваемое в более общем топологическом графе. Перечислим основные преимущества использования графа смежности граней.
- AAG позволяет применить чисто графовый подход к анализу модели. Вместо наглядной геометрической информации мы принимаем более абстрактную перспективу. Абстрагируясь, мы можем где-то даже забыть о геометрической подоплеке решаемых задач и формулировать подзадачи в терминах теории графов. Например, можно ставить задачу о выделении компонент связности, поиске подграфа в графе, нахождении кратчайшего пути и т.д. Таким образом у исследователя вдобавок к геометрической интуиции формируется абстрагированная «графовая».
- Второе преимущество состоит в том, чтобы кэшировать индексы ребер, вершин и граней в структуре AAG для эффективного доступа. Например, граничное представление модели в OpenCascade не содержит уникальных идентификаторов граничных элементов в явном виде. Эти идентификаторы извлекаются в процессе навигации по топологическим структурам, что имеет тенденцию существенно замедлять выполнение программы, если пренебречь кэшированием. Увы, специальной практики для такого кэширования нет, и чаще всего программист, не задумываясь, оперирует хэш-таблицами, содержащими индексы граничных элементов и бессистемно рассеянными в коде продукта. Получается, что индексы объектов модели хранятся вне модели, что доставляет немало хлопот с точки зрения поддержки такого кода и его эффективности. С использованием AAG вы получаете вполне натуральный контейнер для кэширования такого рода данных.
- AAG — это метагеометрическая модель, аккумулирующая знание о фичерах и базовые эвристики для их распознавания. Можно расширить классическое определение атрибутированного графа смежности граней, допустив, что помимо атрибутов выпуклости и вогнутости двугранных углов, эта структура может содержать любые атрибуты вообще. В частности, AAG натурально насыщается информацией о фичерах, т.е. собственно инженерной семантикой изделия. Чем больше знания о конструктивных элементах мы получаем, тем насыщеннее оказывается структура AAG. Это делает граф смежности граней удобным носителем семантики B-Rep, тем самым дополняя граничное представление модели (но, конечно, не заменяя его).
- Модель AAG позволяет отловить патологии смежности, например, невидимые грани, скрытые чисто визуально, но технически присутствующие в геометрической модели.
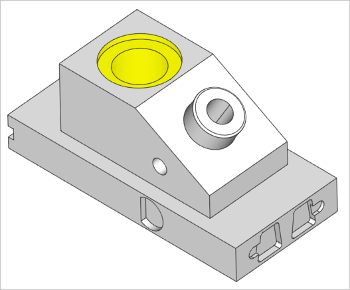
Модель ANC101 с выделенным цилиндрическим отверстием (желтый цвет).
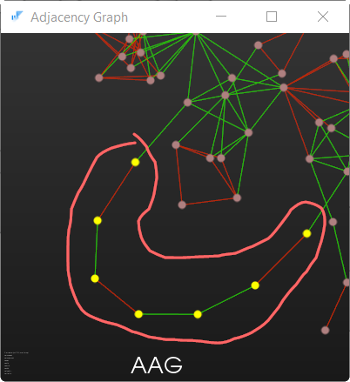
Грани AAG, составляющие цилиндрическое отверстие. Легко видеть, что они образуют непрерывную изолированную цепочку вершин. Это наблюдение позволяет легко вывести правило распознавания изолированных цилиндрических отверстий.
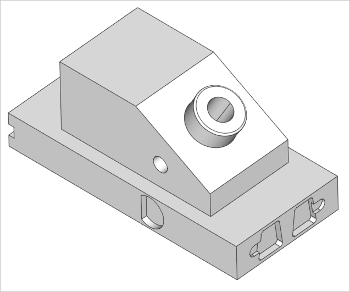
Визуально корректная модель ANC101.
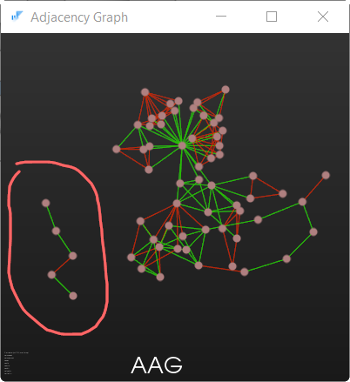
Два компонента связности в AAG. Обведенная группа вершин соответствует невидимым граням, «отрезанным» от основной модели ANC101 в результате некорректной операции редактирования.
Чтобы воспринять AAG как полноценный вспомогательный инструмент, им надо, конечно, попользоваться. Реализация этой структуры почти тривиальна, поэтому не стоит отказывать себе в удовольствии. Кроме того, в вашем распоряжении есть готовый к использованию граф смежности граней для топологических структур OpenCascade (реализован в рамках исследовательского проекта Analysis Situs).