On recognizing canonical surfaces: linear extrusions
"Synthetic geometry is that which studies figures as such, without recourse to formulae, whereas analytic geometry consistently makes use of such formulae as can be written down after the adoption of an appropriate system of coordinates." Felix Klein.
In our previous series, we discussed how to recognize planar and cylindrical surface types. Let's look at a generalized cylinder or a surface of linear extrusion today.
Automatic detection of specific surface types in a CAD model is an essential aspect of feature recognition. Understanding surface types becomes vital for finishing milling as the surface type dictates the class of cutting tool to set up. Linear extrusion surfaces are common in prismatic features of CNC-milled parts. Geometrically, such surfaces are created by sweeping a curve in a constant direction. This surface type is described in the STEP (ISO 10303) standard as follows:
 |
An excerpt from ISO 10303 on the generalized cylinder entity (click to access the paper). |
So far, so good. And, because OpenCascade is STEP-compliant, we may expect to see the instances of the Geom_SurfaceOfLinearExtrusion type in our CAD model's faces. However, this is not always the case. Linear extrusion surfaces are sometimes hiding beneath more general freeform geometries, such as splines or Bézier patches, whose analytical properties reveal nothing about their extrusion nature. At this point, we have to perform canonical recognition, where the extruded surface is the "canonical" type we seek.
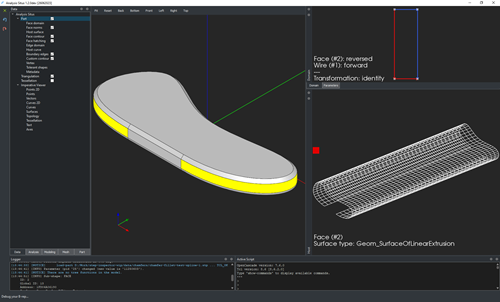 |
Surface of linear extrusion for a CAD face inspected in Analysis Situs (click to enlarge). |
In canonical recognition, there are two key steps:
- To check if a surface in question has the target type.
- To substitute the original surface in the input CAD model with the converted one.
The second stage is optional and can sometimes be skipped to save computation time.
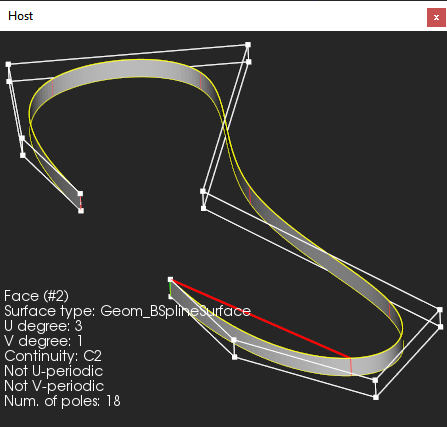 |
Surface of linear extrusion in B-spline form. |
The process of canonical conversion is sometimes referred to as another kind of "shape healing." However, a CAD model's geometrical or topological flaws are not actually "healed" by this algorithm. The geometry of your part will rather be "normalized" during this process to prepare it for upcoming feature recognition and shape editing scenarios. Canonical conversion thereby simplifies the underlying surface types while converting one valid state of geometry to another.
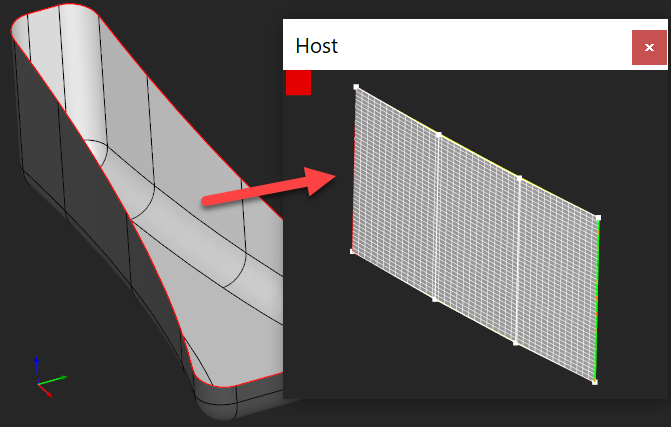 |
A pocket feature with spline walls that can be converted to linear extrusion surfaces. |
With a recent upgrade, the convert-to-canonical command in Analysis Situs can now handle surfaces of linear extrusion. As such surfaces are frequently encountered in prismatic features, this is a significant gain in the cases involving milling axis detection. The direction member field of the base Geom_SweptSurface class contains the intrinsic axis of a linear extrusion surface together with the generatrix curve basisCurve:
Handle(Geom_Curve) basisCurve; gp_Dir direction;
The recognition principle for surfaces of linear extrusion is fairly trivial:
- Take a couple of probe isoparametric lines originating from the midpoint of the face's UV domain.
- Check if one of those isolines is a straight line, while another is not. The straight line gives a potential extrusion direction.
- Use a lot more probe samples to confirm that if we move over the surface, the extrusion direction doesn't change.
 |
Profile sampling for getting max surface curvature. The vertical side wall was converted from spline to a surface of linear extrusion. |
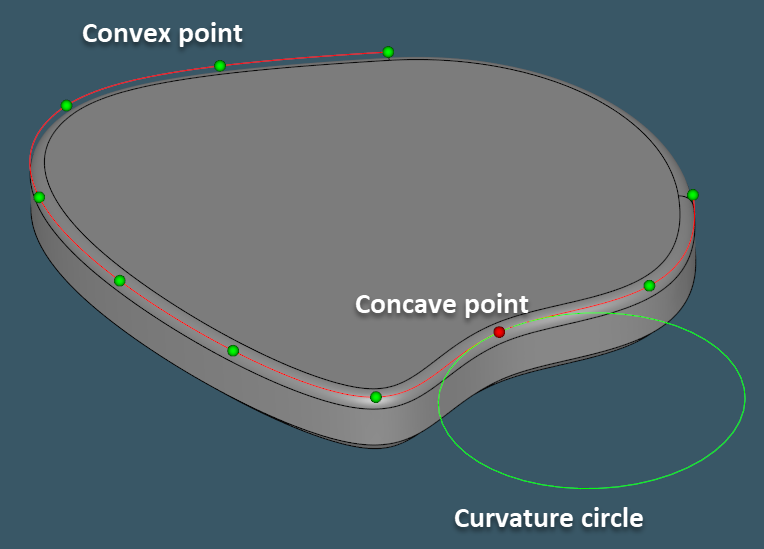
Once a surface of linear extrusion is found, we can use its nice properties to further explore CAD model features. One pretty evident property of such surfaces is that they are not curved in their sweeping direction. Therefore, for manufacturability testing, it would be sufficient to measure surface curvatures over the profile curve alone, reducing the two-dimensional point sampling problem to a single dimension.
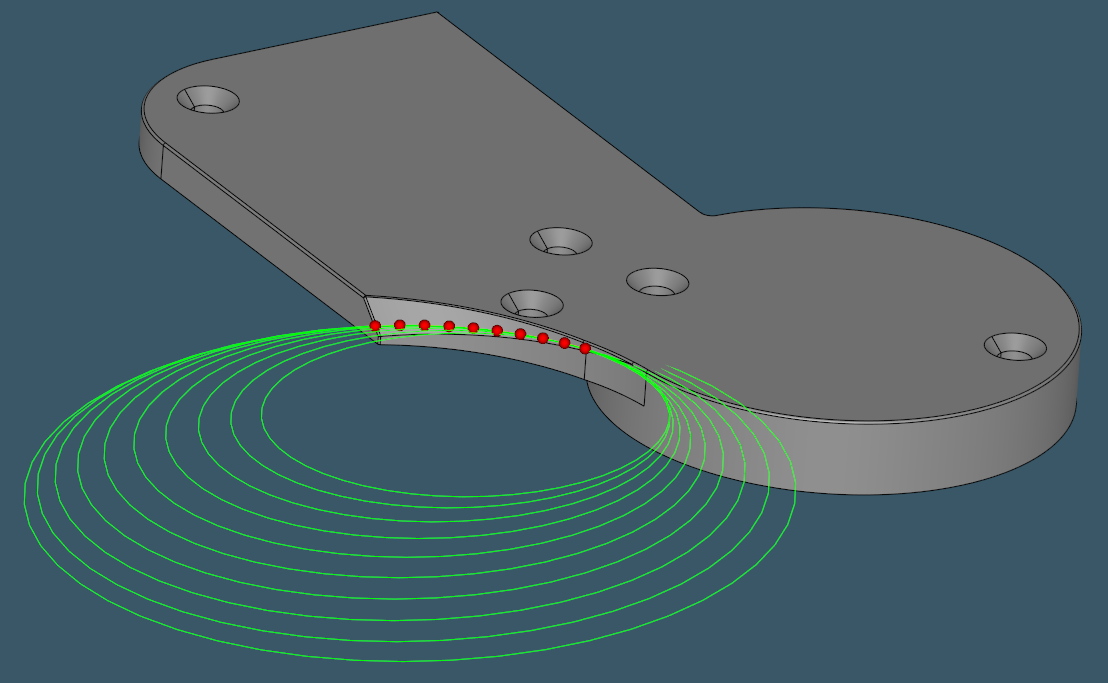 |
Another example with entirely concave profile curve. |
To determine if a probe point is convex or concave, we employ the same method that was previously discussed for surfaces. A probe point on a curve is first projected back to the surface and then the principal curvature values are extracted. As before, after taking into account the topological orientation of a face, we can begin to rely on the curvature sign to conclude if the originating point is convex or concave. To make the extracted information visually clear, we draw little "curvature circles" along the profile curve.
 |
Curvature radii rendered as circles at concave points along profile curves. I cannot resist capturing this little piece of computational art. Just look at these symmetries and tell me if I'm exaggerating. |
It should be noted that the surfaces of linear extrusion are more restricted than, for example, ruled surfaces. One particularly interesting case we came across was false-positive detection of helical surfaces as the surfaces of linear extrusion. Such surfaces are frequently found in the parts with modeled threads.
 |
Elevation verification on a double-curved surface. |
The recognition method we developed examines a surface's "elevation" with respect to the reference axis as measured at the midpoint along the straight surface direction. This extra heuristic allows for the skipping of thread features and eliminates the need of costly and unreliable calculations targeted at reapproxiamting the surface edges.
 |
Elevation verification on a single-curved surface. |
If a surface has no elevation, all probe points are projected into the same position, and the surface is nicely converted. Long twisted surfaces like these are common in engraving features.
 |
Elevation verification on a single-curved surface. |
Want to discuss this? Jump in to our forum.