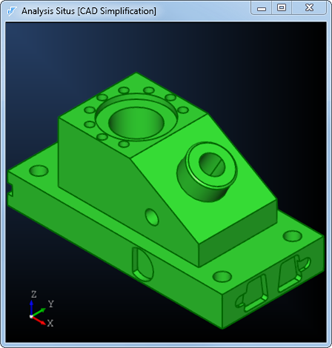
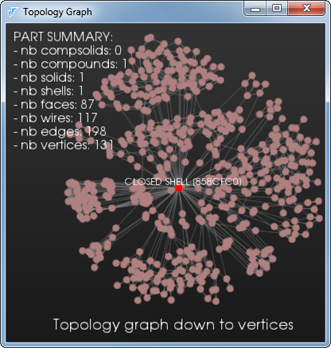
← Научная школа А.А. Андронова и ее значение для мировоззрения ученого

Топология в САПР

Среда, 24 февраля 2016 г. / Просмотров: 5542

Методология / Geometric modeling / История науки и техники / Feature recognition

"To solve many of geometric problems we do not need to know spatial information but what is required to be known is neighborhood or connectivity information termed as topology." (Sandip Jadhav).

История вопроса

В геометрическом моделировании для САПР понятие топологии является одним из центральных. Важно отметить, что ставшее традиционным разделение на геометрию и топологию, не есть исключительная особенность технологии B-Rep. Можно, например, смоделировать заварочный чайник, используя объемные элементы (воксели), либо комбинаторный принцип (CSG), либо что-то совсем оригинальное. В любом случае топология никуда не уходит, ее можно формально определить и плодотворно использовать. Чтобы понять это разделение, следует обратиться к его изначальной идее.

Основной топологический вопрос — принадлежит ли точка телу? Если мы можем ответить на него, то наш подход к моделированию является полным. Если нет, значит выбранный подход никуда не годится.

Отметим сперва, что топология в собственном смысле — это тоже геометрия, однако более общего плана, чем, скажем, Евклидова или проективная геометрии. Уже в XIX веке математикам стало понятно, что пятый постулат Евклида о параллельности прямых не нужен. Будучи выброшенным из исходной аксиоматики, он не помешает возведению стройного геометрического здания, пусть и более причудливой формы. Знаменитый немецкий геометр Феликс Клейн, вступая в должность профессора Эрлангенского университета, прочитал по сложившейся традиции обзорную лекцию о предмете своего научного поиска. Эта лекция теперь известна всему математическому миру как Эрлангенская программа, где Клейн излагает новый, систематический подход к построению геометрии. Согласно его определению, геометрия изучает свойства объектов, инвариантные относительно выбранной группы преобразований. Именно выбранный тип преобразований определяет, какая геометрия у нас получится. Если рассматривать движения, то имеем Евклидову геометрию. Если допустить аффинные преобразования (от латинского «finitas» — конечный, то есть отправляющий в бесконечность исключительно бесконечные же точки), то получится более причудливая, но удобная в САПР аффинная геометрия, уже не отличающая, скажем, два треугольника друг от друга, какими бы они ни были. Дальше идет проективная геометрия с ее дробно-рациональной группой преобразований, позволяющей, в отличие от аффинной группы, отправить уже конечную точку в бесконечность. Нетрудно видеть, что чем изощреннее выбранное преобразование, тем меньше остается в результирующей геометрии того Евклидова духа, к которому мы все привыкли еще со школьной скамьи. Наконец, можно настолько абстрагировать вводимую группу преобразований, что она теряет конкретное математическое выражение, приобретая обобщенную формулировку: «непрерывное преобразование без разрезаний и склеек». Именно здесь и возникает знаменитое преобразование бублика в кофейную кружку (рис. 1). Новая геометрия получает название «топологии», а тополог становится страшно далек от изначальных геометрических задач типа «нарезать земельный участок пополам с соседом».

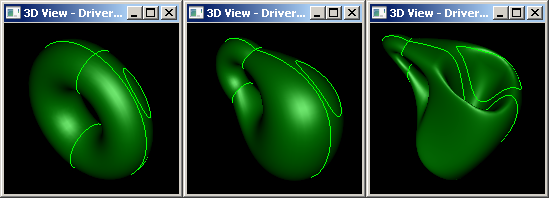
Рис. 1. Превращение бублика в кружку.

Топология как наука образовалась во многом благодаря Анри Пуанкаре, который на излете своего творчества загадал человечеству абстрактную, но очень красивую загадку о трехмерной сфере. Тополог, как уже было сказано, — это ученый высокого абстрактного полета. Но САПР — вещь предельно конкретная, где пока еще не нашлось места трехмерной сфере и многим другим играм изощренного воображения. Почему же мы говорим об этом? Можно понять суть топологии, исходя из ее первоначального названия: «analysis situs», т.е. анализ положения. Топология безразлична к форме объекта (лишь бы соблюдался гомеоморфизм), но, как и любая геометрия, она изучает некоторые инварианты относительно этих взаимно однозначных и взаимно непрерывных преобразований. И такими инвариантами, что существенно для САПР, являются отношения принадлежности. Если точка принадлежит телу, то в результате любого допустимого преобразования (как в лепке из пластилина), это отношение сохранится. Именно это топологическое свойство оказалось столь существенным в практике геометрического моделирования, что топологический язык был введен туда в качестве основного. Теоретики от САПР должны быть знакомы с топологическим формализмом для ведения исследований.

Гомеоморфизм можно мыслить как деформацию пространства. Растягиваем мы его, или сжимаем, принадлежность точки объекту не изменяется, так как она претерпевает те же преобразования, что и ее «носитель».

Насколько известно автору, техническое разделение между концепциями геометрии и топологии для САПР было впервые реализовано в системе BUILD 2 группой исследователей из Кембриджа, известной как «CAD Group». Эту группу образовали три рыцаря геометрического моделирования: Ян Брэйд (Ian Braid), Алан Грэйер (Alan Grayer) и Чарльз Лэнг (Charles Lang). История CAD-группы вполне заслуживает отдельного разговора, так как именно ее усилиям мы в конечном итоге обязаны появлению таких технологически сложных, дорогих и определенно задающих стандарт библиотек, как Parasolid и ACIS. Да, эти библиотеки недоступны отдельно стоящему программисту в его повседневном вычислительно-геометрическом быту. Но важен ведь не сам факт существования каких-то инженерных продуктов с развитой маркетинговой экосистемой и астрономическими годовыми выручками их владельцев. Нам важно другое. Становление этих систем сопровождалось активным научным поиском, в процессе которого были сформулированы сами принципы геометрического моделирования, его метод и своеобразный кибернетический дух. Общедоступной же точкой приложения подобного рода знаний можно считать библиотеку Open CASCADE Technology (OCCT) — на сегодняшний день единственную в своем роде. Все названные системы, так же как и многие другие (C3D, RGK, CGM), произрастают из единого принципа B-Rep, где топология нашла свое отчетливое выражение в виде графа взаимосвязей между примитивными геометрическими объектами.

Такова историческая подоплека этой топологической темы. Посмотрим теперь на предмет разговора живьем.

Знакомьтесь, топологический граф

Итак, граничное представление модели задается топологическим графом, который можно нарисовать. Этот граф играет роль своеобразного скелета, сохраняющегося при гомеоморфизмах формы, то есть при деформациях без разрезаний и склеек. В обзорной статье по поводу библиотеки OpenCascade мы приводили пример такой деформации, переводящей пончик в кофейную чашку (см. также рис. 1). Внимательный читатель должен был заметить, что обе формы задаются в точности одним и тем же топологическим графом. Топологический граф — вещь довольно эзотерическая, особенно, если рассуждать с позиции инженера. Однако с точки зрения геометра это очень важная структура данных, о которой следует поговорить подробно.

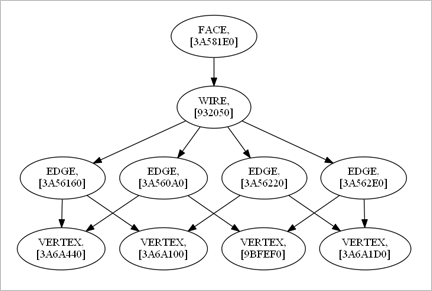
Рис. 2. Топологический граф грани кубика. Каждый узел графа снабжен адресом соответствующей структуры в оперативной памяти.

Узлы графа — это, прежде всего, носители геометрии, такие как грань, ребро или вершина. Носитель может играть и чисто организующую роль, как, например, контур, оболочка или тело. Дуги графа задают отношение принадлежности. Так, контуры принадлежат грани, а ребра содержатся в контурах. Возвращаясь к основному топологическому вопросу о принадлежности точки телу, заметим, что граф сам по себе на этот вопрос не отвечает. Равным образом на этот вопрос не отвечает и «чистая» геометрия, так как в ней не содержится информации о границах. Однако связка графа и геометрии оказывается достаточной, чтобы такая классификация точки относительно тела могла быть выполнена.

Под телом здесь мы понимаем любой объект моделирования, будь то объем пространства или оболочка. Различия между твердотельным и поверхностным моделированием в данном контексте несущественны.

Топологический граф даже очень простых моделей выглядит чудовищно сложным. Визуально работать с ним напрямую невозможно. На рис. 3 изображен топологический граф популярной модели ANC101 (визуализация графа подготовлена при помощи VTK).

Рис. 3. Модель ANC101 и ее топологический граф.

Чем же топологический граф полезен на практике? Чтобы ответить на этот вопрос, давайте разберемся, исходя из каких соображений выбираются вершины, ребра и грани CAD-модели (ведь вариантов их выбора бесконечно много). Все вместе они называются топологическими ограничениями. Топологические ограничения чаще всего отражают конструктивный замысел проектировщика (то, что называют «design intent»). Однако бывает и так, что выбор границ полностью диктуется производящим алгоритмом, а не реальными особенностями формы. В таком случае расположение ребер может показаться неадекватным, так как они очерчивают не те контуры модели, которые ожидались пользователем интуитивно (рис. 4).

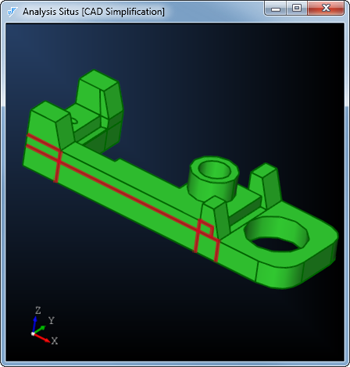
Рис. 4. Избыточные ребра, полученные в результате применения булевых операций (показаны красным цветом). Все эти ребра вызывают недоумение, так как они не несут семантической нагрузки.

Упомянутые выше «интуитивно воспринимаемые особенности» называются конструктивными элементами, или «features». Конструктивный элемент — это стереотипная форма, легко идентифицируемая человеком и совершенно неразличимая для машины.

Термину «feature» непросто сопоставить емкий русскоязычный эквивалент. Более того, даже в английском языке содержание этого термина плавает, так как одни и те же участки формы можно трактовать и как конструктивный элемент, и как базовую геометрию. Пожалуй, наиболее близким по смыслу переводом будет словосочетание «стереотипная форма», подчеркивающее присущую понятию (именно понятию!) «feature» субъективную природу.

Наличие этих элементов может оказаться чрезмерным, а их положение неподходящим с точки зрения, скажем, инженерного анализа. Действительно, при конечно-элементном или гидродинамическом анализе мы стремимся пренебречь мелкими отверстиями, скруглениями и другими особенностями модели, чей результирующий вклад априори невелик. Такие паразитные элементы становятся серьезным препятствием хотя бы из-за того, что генераторы расчетных сеток должны с ними сообразовываться. Возникает ситуация, когда конструктивный замысел модели не соответствует расчетному замыслу (рис. 5).

Рис. 5. Мелкие отверстия должны быть удалены перед инженерным расчетом.

Чтобы перейти к расчетной модели обычно требуется избавиться от нежелательных конструктивных элементов вручную, осуществляя тем самым некоторое упрощение формы (CAD simplification). Такое упрощение чисто технически состоит в том, что изменяется топологический граф модели, а часто и ее геометрия. Скажем, для удаления простейшего цилиндрического отверстия, как на рис. 5, достаточно изъять из графа все соответствующие ему узлы. Таким образом наша геометрическая задача оказывается тесно связанной с теорией графов.

Заметим также, что ситуаций, изображенных на рис. 4, следует избегать, так как дополнительные топологические ограничения чрезмерно усложняют граф. Кроме того, лишние ребра нарезают оболочку тела на регионы, которые не имеют конструктивной ценности сами по себе, тем самым размывая изначальный замысел проектировщика. Пожалуй, здесь следует сформулировать эмпирическое правило: топология CAD-модели должна отражать замысел проектировщика минимально возможным набором границ.

Граф смежности граней

Выше мы рассмотрели топологический граф и убедились в его неохватной сложности. Даже примитивные модели, такие как ANC101, содержат столько границ в своем B-Rep описании, что не возникает никакого желания использовать их топологические графы в явном виде. С другой стороны, для описания стереотипных форм модели этого не требуется. Мы можем обойтись графами, содержащими только грани, плюс некоторую дополнительную информацию. Здесь мы вводим в рассмотрение граф производный от топологического — граф смежности. Узлами такого графа являются только грани, а дугами — отношения смежности между ними.

Общий топологический граф дает полную структуру B-Rep, тогда как граф смежности — только отношения между гранями. Топологический граф B-Rep можно назвать графом принадлежности, где смежность ребер, граней и даже тел выражается наличием у одного узла нескольких входящих дуг. Граф принадлежности является ориентированным, тогда как граф смежности — нет.

Граф смежности всей CAD-модели можно использовать для поиска стереотипных форм, таких как отверстия, карманы, уголки и проч. Идентификация этих форм на «немой» модели, то есть в условиях, когда история построения недоступна, — одна из важнейших задач САПР.

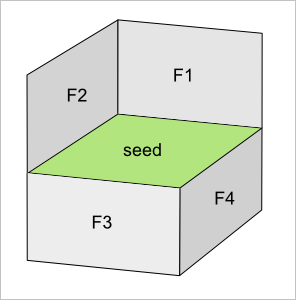
Рис. 6. Смежные грани для некоторой избранной грани, именованной «seed».

Рассмотрим композицию из пяти граней, показанную на рис. 6. Нас интересуют соседи для грани, именованной «seed» (т.е. «начало»). Нетрудно вычертить отвечающий данной композиции граф смежности (рис. 7).

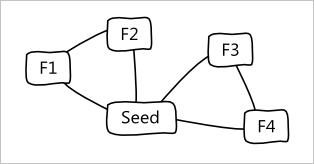
Рис. 7. Граф смежности для граней, изображенных на рис. 6.

Вернемся к модели ANC101. В ней содержится 87 граней, поэтому граф смежности (рис. 8) оказывается существенно проще графа принадлежности (рис. 3). Этот граф явно или неявно используется теми геометрическими алгоритмами, которые содержат топологический переход от грани к грани. В качестве примера можно привести алгоритмы создания траекторий для режущих инструментов, или автоматизированный поиск конструктивных элементов. Последний пример особенно удачен, так как во многих случаях этот поиск сводится к выделению подграфов смежности, отвечающих той или иной стереотипной форме.

Рис. 8. Граф смежности для модели ANC101.

Следует заметить, что работа по идентификации конструктивных элементов (feature identification) началась в то же время, когда зародилось само разделение на геометрию и топологию САПР. Исследования, направленные на автоматический поиск стереотипных форм, производились все той же незабвенной CAD-группой из Кембриджа в лице А. Грэйера и Л. Киприанова (L. Kyprianou). Концепция же графа смежности применительно к распознаванию стереотипных форм была введена Джоши (S. Joshi) и Чэнгом (T. Chang) в 1988 г. («Graph-based heuristics for recognition of machined features from a 3D solid model», Computer Aided Design).

Геометрия против топологии

Всякому, кто занимается алгоритмами для САПР, следует твердо уяснить различие между геометрией и топологией. В топологии нас не интересует форма, нам интересны только логические взаимосвязи между объектами. Топология в САПР — это такие швейные нитки, собирающие воедино лоскутное одеяло B-Rep. Мы отметили выше, что топологическое преобразование состоит в таком изменении формы, когда материал не претерпевает разрезаний и склеек. Любопытно, что установление топологических ограничений само по себе состоит в разрезании (удалении ненужного материала граней) и склейке (настройке смежности).

На интуитивном уровне понять различие между топологией и геометрией помогает следующая аналогия, позаимствованная мною у Тома Верстрате (Tom Vertsraete). Представим себе схему лондонского метро. Обратимся сначала к карте, где показано реальное расположение станций и веток (рис. 9).

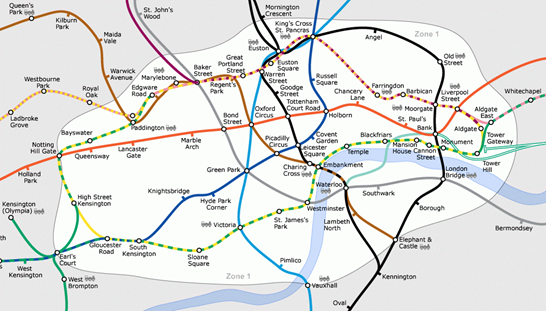
Рис. 9. Лондонское метро с точной географической привязкой (геометрия).

На практике же нас интересует только взаимное расположение станций и веток, чтобы мы могли правильно проложить маршрут из точки A в точку B. Реальная форма пути не имеет значения (рис. 10).

Рис. 10. Схема лондонского метро (топология).

Конечно, топологические схемы стремятся сообразовать с реальным географическим положением веток, иначе турист окончательно запутается. Поэтому рисунки похожи, и Темза тоже никуда не исчезла. Однако топологическая композиция всегда преобразуется таким образом, чтобы быть максимально читабельной. Подобным образом мы рисуем и наш абстрактный топологический граф, стремясь распутать плотный клубок ребер и максимально изолировать вершины на чертеже, чтобы сделать его более внятным. Однако внятность топологического чертежа не имеет никакого отношения к адресуемой им геометрии.