Re-Shape как базовое средство прямого редактирования
"It's not possible to modify a Shape... It's a choice in opencascade, the shape can not be modified..." (фраза с официального форума компании-разработчика OpenCascade).
Нужда в средствах прямого редактирования моделей возникает нередко и в разных контекстах. Примером может послужить сценарий преобразования конструкторской модели в расчетную, когда подавляются незначительные с точки зрения анализа элементы геометрии, такие как фаски, скругления, отверстия и проч. Если опираться здесь на историю построения модели в оригинальной CAD-системе, то при удалении ее конструктивных элементов (фичеров) будет выполнено глобальное перестроение, что, конечно, неэффективно. Кроме того, возможны сценарии, когда история построения модели оказывается недоступной (в этом случае геометрию иногда называют «немой»). Возникает задача редактирования формы изделия (да и не только формы), исходя из нее самой. Мы специально ограничиваемся здесь рассмотрением РЕДАКТИРОВАНИЯ, противопоставляя его МОДЕЛИРОВАНИЮ, так как прямое моделирование — задача куда более сложная, а обсуждение пользы этого подхода и его значимости является источником бесконечных спекуляций и споров.
Что такое прямое редактирование? Это ЛОКАЛЬНАЯ модификация CAD-модели на уровне ее граней, ребер и вершин. Скажем, такие операции как удалить грань, «сшить» несколько ребер или объединить грани в одну — все это примеры базовых алгоритмов прямого редактирования. Заметим здесь, что любое геометрическое ядро поддерживает эти операции, так как они есть основа всего. Им надстоят так называемые эйлеровы операторы, которые уже не просто вносят формальные изменения в топологию модели, но и «следят» за тем, чтобы не нарушалась топологическая корректность.
В этой и других заметках данной серии мы поговорим о прямом редактировании на примере библиотеки OpenCascade. Забегая вперед, заметим, что каких-то особо развитых средств прямого редактирования в этой библиотеке нет, но она дает нам достаточно прочный фундамент для создания подобных средств. Мы начнем с неинтеллектуального, но базового инструмента — BRepTools_ReShape.
Знакомьтесь, Re-Shape
Утилита BRepTools_ReShape была задумана как инструмент для локальной модификации модели с целью ее коррекции. Задача коррекции обычно возникает на этапе обмена данными между САПР-системами с различными геометрическими ядрами. Практика показала, что Re-Shape имеет гораздо более широкое применение в алгоритмах геометрического моделирования. Мы будем говорить, что Re-Shape полезен всюду, где речь идет о прямом (или «динамическом») редактировании модели (главное правильно расставить акценты, не так ли?).
Инструмент Re-Shape предоставляет две базовые операции:
- УДАЛЕНИЕ топологического элемента (грани, контура, ребра, вершины и т.д.)
- ЗАМЕНА топологического элемента на другой или коллекцию других.
Архитектура взаимодействия пользователя с данным классом такова, что сначала Re-Shape накапливает запросы на модификацию топологии, после чего единственным вызовом метода Apply() запрошенная модификация реализуется. Внутри класса Re-Shape мы обнаруживаем хэш-таблицы, хранящие запросы пользователя на изменение топологических объектов. Модификация осуществляется путем последовательной замены всех топологических элементов модели на их образы сверху-вниз, то есть, начиная, скажем, от твердого тела вплоть до вершин.
Рассмотрим такой пример. На рис. 1 показана широко известная модель ANC101, из которой мы желаем удалить некоторые цилиндрические отверстия пренебрежимого диаметра.
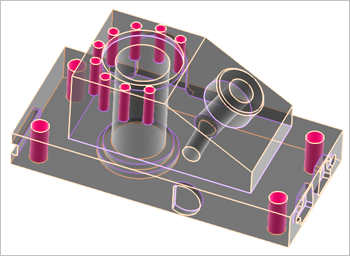
Рис. 1. Модель ANC101. Отверстия, подлежащие удалению, окрашены алым цветом.
Удаление граней приводит к тому, что в модели образуются дыры (рис. 2). Удобство B-Rep здесь проявляется в том, что эти дыры уничтожаются без привлечения дополнительных геометрических построений. Достаточно удалить внутренние контуры на несущих гранях. Заметьте, что на полигональных моделях этот копеечный вопрос уже требует привлечения некоторых, пусть базовых, но все-таки средств вычислительной геометрии.
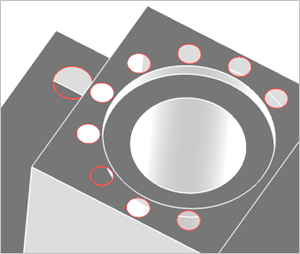
Рис. 2. Модель ANC101 после уничтожения граней, представляюших отверстия. Свободные ребра показаны красным цветом.
Итак, для «зашивания дыр» нам следует удалить также внутренние контуры, а значит и содержащиеся в них ребра и вершины. Учитывая, что в корректных B-Rep моделях смежность ребер реализована посредством разделяемой (shared) структуры данных, удаление ребра одной грани приведет к удалению ребра другой. Тем самым красные границы на рис. 2 будут уничтожены, и модель снова станет условно водонепроницаемой (рис. 3). В скобках отметим, что смежность реализуется НЕ на уровне контуров, а на уровне низлежащих ребер, и поэтому удаление контура одной грани приведет, вообще говоря, к появлению пустого контура на смежной (рис. 6). Недопущение пустых топологических объектов должно быть реализовано в утилите Re-Shape.
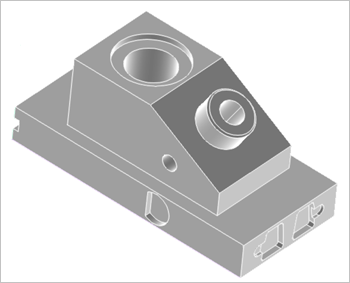
Рис. 3. Модель ANC101 после топологической редукции.
Повторимся, что ни о каких геометрических построениях здесь речи не идет. Отверстия были удалены из модели путем простейшей топологической редукции, то есть иссечением из топологического графа всех «лишних» структур. Такая операция ничего не стоит с вычислительной точки зрения и крайне проста в реализации.
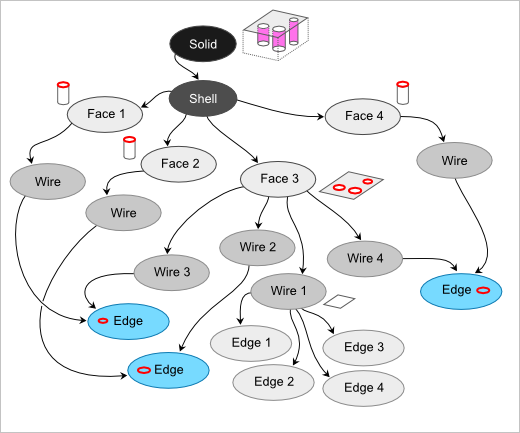
Рис. 4. Фрагмент топологического графа некоторой модели с отверстиями.
На рис. 4 показана выдержка из топологического графа некоторой абстрактной модели. Рассматривается твердотельный объект (Solid), содержащий единственную оболочку (Shell). В оболочке есть некоторое количество граней (Face), задающих геометрическую форму тела, причем каждая грань содержит не менее одного контура (Wire). Контур, в свою очередь, набирается из ребер (Edge), которые могут принадлежать сразу двум родителям (такие ребра подкрашены голубым цветом на рис. 4). Топологическое иссечение с целью подавления отверстий должно уничтожить все вершины, ребра и грани, отмеченные красным цветом на рис. 5.
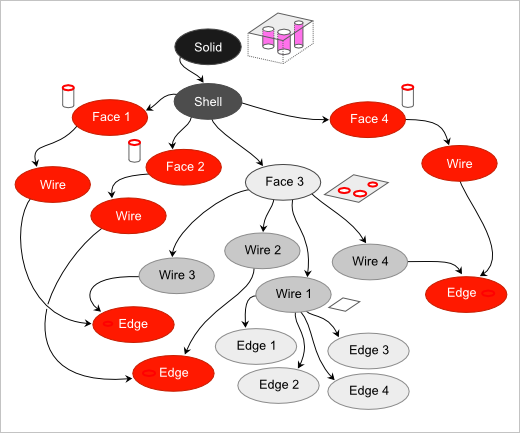
Рис. 5. Элементы топологического графа, отмеченные для иссечения.
Ситуация с топологическим графом после редукции показана на рис. 6. Заметьте, что остались «висячие» контуры, которые не содержат ни геометрии, ни топологии. Чаще всего от них также необходимо избавляться.
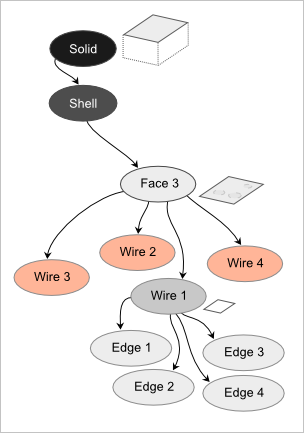
Рис. 6. Элементы топологического графа после редукции.
«Трудный» фичер
Выше мы рассмотрели случай, который часто встречается на практике, но все-таки является немного игрушечным. Дело в том, что чисто топологическое иссечение не всегда достаточно для подавления даже примитивных отверстий. Действительно, если отверстие оказывается помещенным на стыке нескольких граней (рис. 7), то внутренний контур, подлежащий уничтожению, отыскать нельзя — его нет. В этом случае, однако, существует некий импринт отверстия на несущих гранях, который является своеобразной подсказкой аля «здесь был фичер». Недаром в некоторых научных статьях, посвященных распознаванию конструктивного замысла по «немой» геометрии, подчеркивается, что ребра модели — это память модели. Кое-что они могут нам рассказать.
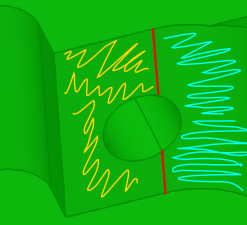
Рис. 7. «Трудный» фичер (отверстие) на стыке двух граней (заштрихованы).
Итак, есть фичеры, для удаления которых чисто топологические операции оказываются бессильными. Для подавления этих конструктивных элементов приходится задействовать более трудоемкие и менее надежные по своей сути алгоритмы вычислительной геометрии. Туда, где отработала артиллерия топологической редукции, вводятся войска геометрических алгоритмов и начинается не особо благодарное дело по восстановлению связности и корректности тела (неблагодарное, т.к. статистически менее вероятный «трудный» фичер требует более серьезных алгоритмов подавления, чем те, что работают на удалении простого, «мягкого» фичера).
Что-то еще?
«Трудный» фичер — это внятная иллюстрация тех задач, которые решаются в контексте динамического (прямого) редактирования CAD-модели. Но это частность. Для расширения списка укажем такие задачи, как подавление скруглений, изменение их радиуса, замена скруглений на фаски, выталкивание и вдавливание граней (дуэт операций «push / pull») и многое другое. Все перечисленное — ЛОКАЛЬНЫЕ операции, замысел которых состоит в том, чтобы быть как можно более эффективными за счет работы лишь в малой окрестности CAD-модели.
Подходит ли OpenCascade для решения этих задач? Безусловно, да, так как в этой библиотеке есть существенный набор средств для реализации алгоритмов динамического редактирования. Достаточен ли этот набор? Нет. Есть ли готовые решения в библиотеке? Скажем, операция интеллектуального удаления грани? Нет, готовых решений не ждите, но трудности, связанные с реализацией того или иного сценария динамического редактирования модели во многом иллюзорны.