← Еще один русскоязычный ресурс по Open CASCADE Technology

Топология OpenCascade

Вторник, 7 октября 2014 г. / Просмотров: 4250

Взгляните на схематическое изображение топологических структур OCCT:

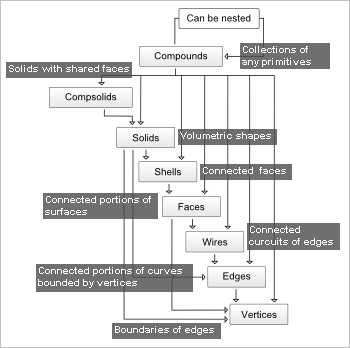
Теперь на изображение топологических структур ACIS:

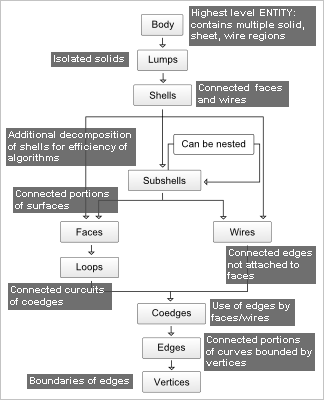
Интересно проверить, как это выглядит в других библиотеках, например, в Parasolid или CGM. Но уже из приведенных картинок становится очевидно, что единый принцип B-Rep вовсе не подразумевает единственно правильного способа его технической реализации. Смежность вершин, ребер и (редко) граней, каждый моделер представляет по-своему, исходя из каких-то разумных соображений. Так, например, топологическая структура ACIS с легкостью может быть использована не только для представления объемных моделей и оболочек, но также и для каркасного моделирования. Это нетрудно видеть из правой ветки для объектов Subshells — там нет граней как таковых. В OCCT все несколько иначе. Мы могли бы смоделировать каркасный объект, просто наполняя некоторую сборку (Compound) набором циклов (Wires). Однако это будет всего-лишь коллекция из несвязанных друг с другом примитивов. В ACIS же мы имеем честный твердотельный объект (Lump), состоящий из честной же оболочки (Shell). Хотя и в OCCT нетрудно видеть, что твердотельный объект (Solid) допускает наличие в нем ребер (Edges), однако не допускает наличие циклов (Wires). Более того, оболочка (Shell) в OCCT уже лишена этих привелегий. Так что разница все-таки есть, но она в деталях.

Общий же принцип «лоскутного одеяла» совершенно идентичен, что в ACIS, что в OCCT, что в любой другой библиотеке, реализующей граничное представление для геометрического моделирования. Рассмотрим произвольную твердотельную модель, то есть набор граней, отделяющих некоторый объем пространства:

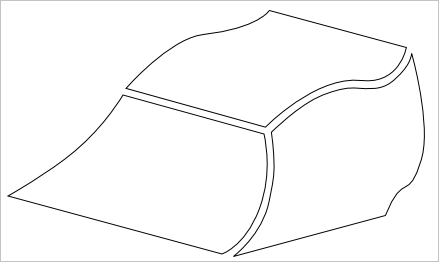
Здесь между гранями мы видим условные зазоры, подчеркивающие, что модель B-BRep не является «водонепроницаемой» в силу самой своей природы. Чтобы понять, как именно хранится топологическая информация в OCCT, рассмотрим две смежные грани. И прежде всего обратим внимание на параметрические поверхности, которые их образуют.

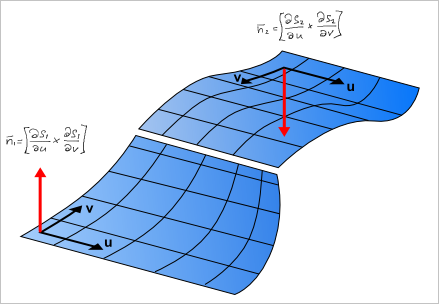
Криволинейные координаты U и V для каждой поверхности выбраны так, чтобы нарушить принцип согласованности нормалей. Для соседних граней они «смотрят» в разные стороны. Если допустить, что рассматриваемые поверхности заданы в прямоугольной области определения (как, например, NURBS), то договоримся выбирать положительное направление обхода контура так, чтобы материал оставался слева по ходу движения в параметрическом пространстве.

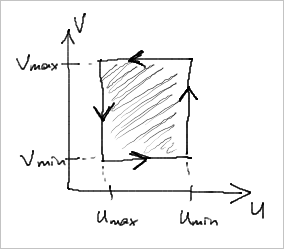
Зачем вообще выбирать ориентацию контура? Это нужно для того, чтобы иметь простой способ для представления отверстий. Договариваясь, что материал находится слева, легко сориентировать контур так, чтобы ограничиваемая им площадь оказалась справа.

Очевидно, в силу гомеоморфизма, что такое направления обхода, будучи рассмотренным в 3D, формулируется следующим образом: положительным направлением обхода считается то, при котором материал поверхности остается слева по ходу движения, глядя со стороны естественной нормали к поверхности. Под естественной нормалью здесь понимается векторное произведение частных производных поверхности в данной точке. Естественная нормаль полностью определяется выбранной параметризацией.

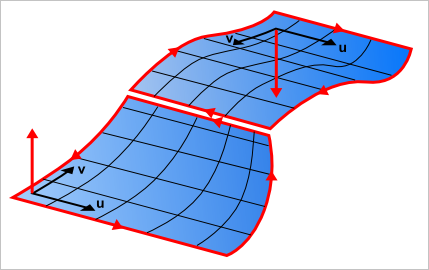
Отсюда мы видим, что смежное ребро вовсе не обязательно имеет противоположные направления обхода на родительских гранях, будучи рассмотренным в 3D. Мы также видим, что одно и то же ребро представлено двумя параметрическими кривыми, соответствующими максимальным значениям параметра V на обеих поверхностях. Добавим теперь к этим двум параметрическим представлениям третье — уникальную кривую в 3D. Без этой кривой определение ребра не будет считаться корректным в OCCT.

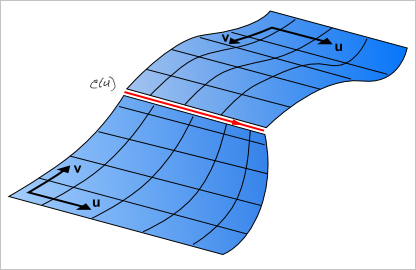
Если натуральная ориентация кривой не совпадает с ожидаемой (это проверяется для каждой из смежных граней), ее можно изменить на противоположную, выставляя флаг REVERSED. Если все в порядке, то выставляется флаг FORWARD. В рассматриваемом случае оба вхождения ребра (2 экземпляра TopoDS_Edge) для каждой грани будут иметь ориентацию REVERSED (если ориентация их родительского цикла выставлена в FORWARD). Хотя, в общем случае, ориентации могут различаться. Именно последнее обстоятельно приводит нас к тому, что помимо самого ребра, необходимо хранить его вхождения в ту или иную грань.

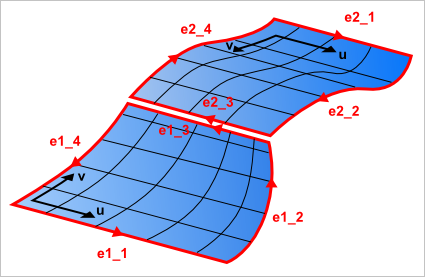
Итак, само ребро представляется классом TopoDS_TEdge, который может входить в несколько циклов (Wires). Вхождение же ребра в тот или иной цикл (грань) реализуется классом TopoDS_Edge. Аналогичным образом дела обстоят и со всеми остальными топологическими примитивами. Следующий скетч иллюстрирует техническую реализацию топологической структуры:

Стрелочками показано вхождение через TShape. Точками — прямое вхождение через поле класса. Реальная связка топологии и геометрии осуществляется через классы BRep_TEdge, BRep_TVertex и BRep_TFace — только эти топологические примитивы имеют ассоциированную геометрию.