Совмещение цилиндра с облаком точек
Библиотека OpenCascade пригодна к решению задач обратного (реверсивного) инжиниринга. Развитых средств конвертации полигональных моделей в точные в ней нет, но для их построения можно использовать математическое обеспечение библиотеки. Рассмотрим типовую задачу совмещения цилиндра с облаком точек. В простейшей постановке будем считать, что начальное (грубое) приближение задано и нужно уточнить его радиус. Задача игрушечная, но демонстрирующая использование некоторых важных базовых инструментов.
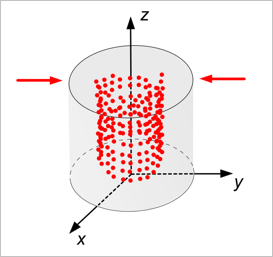
Начнем с подготовки тестового облака. Для этого изготовим цилиндрическое тело и пробежимся двойным циклом по параметрическому пространству его боковой грани, снимая в каждой точке значение по поверхности. Этот примитивный способ дает хорошо структурированное облако точек, редко встречающееся в реальных данных оцифровки. Чтобы приблизиться к реальности следует внести шум в положение точек. Один из способов сделать это представлен листингом ниже:
void SamplePoints(const TopoDS_Face& cylFace,
std::vector<gp_Pnt>& points)
{
Handle(Geom_CylindricalSurface)
cylSurface = Handle(Geom_CylindricalSurface)::DownCast( BRep_Tool::Surface(cylFace) );
// Get parametric bounds of the face
double uMin = 0, uMax = 0, vMin = 0, vMax = 0;
BRepTools::UVBounds(cylFace, uMin, uMax, vMin, vMax);
const double uStep = (uMax - uMin)*0.01;
const double vStep = (vMax - vMin)*0.01;
// Random number generator
math_BullardGenerator RNG;
// Loop in the parametric space to sample the surface
double v = vMin;
while ( v < vMax )
{
double u = uMin;
while ( u < uMax )
{
// Noised value
const double uNoised = u + RNG.NextReal() / (uMax - uMin);
const double vNoised = v + RNG.NextReal() / (vMax - vMin);
// Evaluate
gp_Pnt P;
gp_Vec d1u, d1v;
cylSurface->D1(uNoised, vNoised, P, d1u, d1v);
// Noised normal
const gp_Vec nNoised = (d1u^d1v).Normalized()*RNG.NextReal();
// Noised point
P = P.XYZ() + nNoised.XYZ();
// Store
points.push_back(P);
u += uStep;
}
v += vStep;
}
}
Обратите внимание на использование генератора случайных чисел Булларда. Мы уже говорили о нем в заметке о нахождении расстояния между двумя параметрическими кривыми. Внесение шума дает картинку следующего вида:
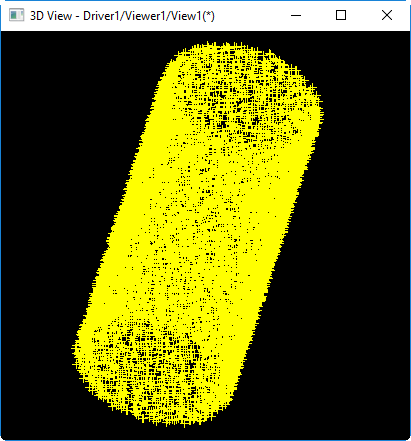
Построим начальное приближение как цилиндр меньшего или большего охвата. Допустим, что ось грубого приближения уже подобрана и будем управлять только радиусом. Для совмещения цилиндра и облака нужно решить элементарную задачу минимизации, где целевой является функция суммарного расстояния от точек до поверхности. Для применения методов оптимизации библиотеки OpenCascade, эту функцию следует оформить в виде класса-наследника math_MultipleVarFunction:
//! Function for evaluation of distance between the point set and the target
//! cylindrical surface.
class SquaredDistFunc : public math_MultipleVarFunction
{
public:
SquaredDistFunc(const std::vector<gp_Pnt>& points,
const Handle(Geom_CylindricalSurface)& cylSurf)
: math_MultipleVarFunction()
{
m_points = points;
// Copy surface not to affect the original geometry
m_surface = Handle(Geom_CylindricalSurface)::DownCast( cylSurf->Copy() );
}
public:
virtual int NbVariables() const
{
return 1;
}
virtual bool Value(const math_Vector& X, double& F)
{
// Apply new radius
m_surface->SetRadius( X(1) );
// Prepare analysis tool
ShapeAnalysis_Surface sas(m_surface);
// Calculate average distance
double dist = 0;
for ( size_t pidx = 0; pidx < m_points.size(); ++pidx )
{
sas.ValueOfUV(m_points[pidx], 1.0e-6);
dist += Square( sas.Gap() );
}
// Set function value
F = dist;
return true;
}
protected:
std::vector<gp_Pnt> m_points; //!< Points to fit into.
Handle(Geom_CylindricalSurface) m_surface; //!< Surface to fit.
};
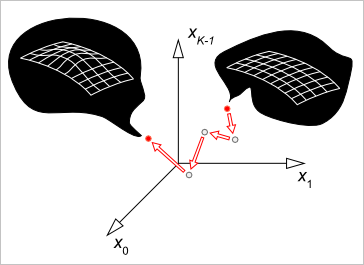
Принцип оптимизации: точка в пространстве параметров соответствует новой поверхности. В нашем случае пространство одномерно, а поверхность является примитивным цилиндром.
Заметьте, что оптимизируемая поверхность изменяет радиус при каждом «испытании». Закон выбора следующего значения остается за кадром — это решает метод оптимизации. Код инициализации и вызова оптимайзера приведен ниже:
void Optimize( ... )
{
...
math_Vector rMin(1, 1), rMax(1, 1);
rMin(1) = 0.0;
rMax(1) = 100.0;
//
math_Vector rStep(1, 1), rDelta(1, 1);
rStep = (rMax - rMin)*0.01;
// Prepare objective function
SquaredDistFunc distFunc(points, cylSurf);
// Outputs
math_Vector rOut(1, 1);
// Run optimization
double distance;
math_PSO PSO(&distFunc, rMin, rMax, rStep);
PSO.Perform(rStep, distance, rOut);
std::cout << "Optimized radius: " << rOut(1) << std::endl;
std::cout << "Best fitness (squared deviation): " << distance << std::endl;
}
Здесь используется негладкий глобальный метод PSO (Particle Swarm Optimization), о котором мы говорили в прошлом. Результат оптимизации приведен на следующей картинке.
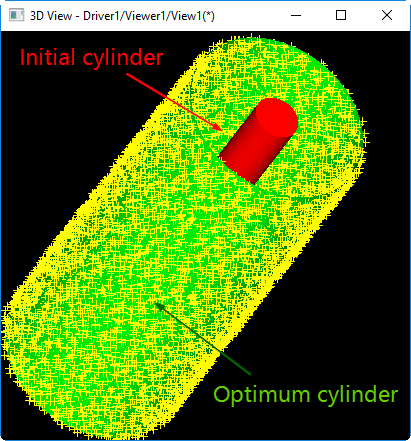
Используя математическое обеспечение геометрического моделирования, вы значительно расширяете спектр решаемых задач. В будущем мы не раз вернемся к задачам обратного инжиниринга, решение которых, хотя и требует разработки дополнительных методов, но отлично укладывается в экосистему OpenCascade.