Немногообразная топология в STEP
Мы продолжаем разговор о средствах трансляции CAD-данных в библиотеке OpenCascade. Самым разработанным и широко используемым нейтральным форматом, как известно, является STEP (ISO 10303). Этот формат позволяет обмениваться не только геометрией, но и мета-данными, причем выразительные возможности формата широки настолько, что для успешной трансляции желательно следовать специально разработанным «рекомендованным практикам». Чтение и запись мета-данных — это серьезная проблема, требующая кропотливого изучения стандарта и внимательного отношения к самой программной архитектуре моделирующего движка. Но и уровень чистой геометрии «полон опасностей». Сегодня мы разберемся с тем, как STEP-транслятор OpenCascade умеет обращаться с немногообразной топологией B-Rep.
Немного немногообразности
Двумерное многообразие (2-многообразие) — это топологический термин, привлекаемый для выражения простой, в сущности, идеи. Упрощенно говоря, если у нас есть 2-многообразие, значит любое ребро модели входит не более, чем в 2 грани (см. рис. 7 из заметки о булевых операциях). Это нестрогое определение, но оно позволяет уловить суть. Более строго, два-многообразие — это топологическое пространство, окрестность каждой точки которого локально гомеоморфна открытому кругу.
Немногообразная топология нечасто встречается в классическом геометрическом моделировании, так как реально существующие объекты все сплошь многообразны. Немногообразность — это вообще продукт идеализации, когда, например, тонкостенное тело заменяется поверхностным аналогом. Идеализации подобного рода хорошо знакомы расчетчикам, применяющим конечно-элементный анализ на идеализированных оболочечных моделях вместо аккуратных, но бестолковых конструкторских. Для построения этих идеализаций существуют специальные инструменты, и чаще всего речь идет о выведении «срединных поверхностей» с последующей склейкой соседних. Эта склейка и есть тот самый процесс, при котором 2-многообразие претерпевает качественное изменение, становясь немногообразным объектом. Заметим в скобках, что оно не превращается при этом, например, в 3-многообразие, как можно было бы вообразить. Просто оно лишается своего изначального свойства быть 2-многообразием.
Поддержка немногообразности в системе геометрического моделирования реализуется на уровне структур данных и никакой сложности не представляет (поэтому не верьте рекламным проспектам!). Все сложности начинаются потом, когда вы захотите использовать немногообразные модели в геометрических алгоритмах или для обмена данными. С алгоритмами мы пока разбираться не станем, а вот на обмен данными посмотрим пристально, так как этот вопрос по существу ключевой. Предположим, вы использовали OpenCascade для создания немногообразной CAD-модели с тем, чтобы построить на ней расчетную сетку и запустить некий анализ. В таком случае вам пригодится правильным образом записанный STEP-файл, в котором свойство немногообразности сохранено без искажений.
Чтобы различить немногообразное тело в OpenCascade, можно воспользоваться, например, таким кодом:
void find_nonmanifold_edges(const TopoDS_Shape& shape,
TopTools_IndexedMapOfShape& nmEdges)
{
// Get child-parent relationships
TopTools_IndexedDataMapOfShapeListOfShape M;
TopExp::MapShapesAndAncestors(shape, TopAbs_EDGE, TopAbs_FACE, M);
// Check for every edge the number of its owning faces
const int nEdges = M.Extent();
for ( int e = 1; e <= nEdges; ++e )
{
const TopoDS_Edge& E = TopoDS::Edge( M.FindKey(e) );
//
if ( BRep_Tool::Degenerated(E) )
continue;
const int nOwningFaces = M.FindFromIndex(e).Extent();
if ( nOwningFaces > 2 )
nmEdges.Add(E);
}
}
В результате коллекция nmEdges окажется заполненной немногообразными ребрами. Проверка очень проста, и, заметьте, она не опирается на какие-либо специфические структуры данных, например, COMPSOLID (TopoDS_CompSolid), как можно было бы предположить.
Немногообразность, ключ на старт
По умолчанию режим трансляции немногообразной геометрии в OpenCascade выключен. Для активации этого режима есть два тумблера:
| read.step.nonmanifold {0, 1} | Активирует чтение немногообразной геометрии. |
| write.step.nonmanifold {0, 1} | Активирует запись немногообразной геометрии. |
Рассмотрим игрушечный пример, позволяющий выявить различия между двумя режимами. Начнем с моделирования простейшего немногообразного объекта в OpenCascade. Документация библиотеки, к сожалению, молчит о том, как можно воспользоваться поддержкой немногообразности, хотя функциональность эта, безусловно, полезна и как минимум достойна упоминания. Первое, что приходит в голову — использовать булевы операции, которые, как известно из теории, дают, вообще говоря, немногообразный результат. Запускаем Draw, пробуем булево сложение:
Draw> pload ALL Draw> box a 1 1 1 Draw> box b 1 0 0 1 1 1 Draw> bfuse r a b
Скоро, однако, выясняется, что результат объединения двух тел — это обыкновенный многообразный объект, ничего интересного. Булев алгоритм оказался достаточно продвинутым, чтобы уничтожить перегородку между двумя операндами, хотя в данном случае это нам не нужно. Чтобы преодолеть эту тонкость, воспользуемся менее очевидным набором команд, которые, по существу, выполняют все ту же булеву операцию, исключая этап изъятия «лишних» топологических элементов.
Draw> bclearobjects Draw> bcleartools Draw> baddobjects a b Draw> bfillds Draw> bbuild r
Получилось. Результирующее тело имеет 4 немногообразных ребра (рис. 1), каждое из которых принадлежит сразу трем граням.
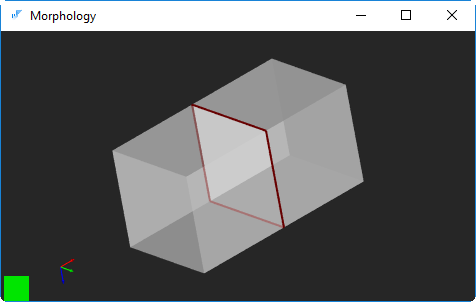
Рис. 1. Немногообразная геометрия, полученная булевым объединением. Немногообразные ребра подкрашены красным цветом.
Продолжим веселье и построим модель, в которой одно из ребер принадлежит сразу четырем граням (рис. 2).
Draw> box a 1 1 1 Draw> box b 1 0 0 1 1 1 Draw> box c 0 0 1 1 1 1 Draw> box d 1 0 1 1 1 1 Draw> bclearobjects Draw> bcleartools Draw> baddobjects a b c d Draw> bfillds Draw> bbuild r
Результат содержит 33 ребра (рис. 3), что, как нетрудно убедиться, соответствует нашим ожиданиям.
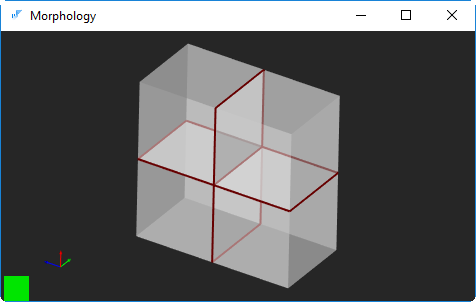
Рис. 2. Еще одна немногообразная модель, полученная склейкой четырех кубиков.
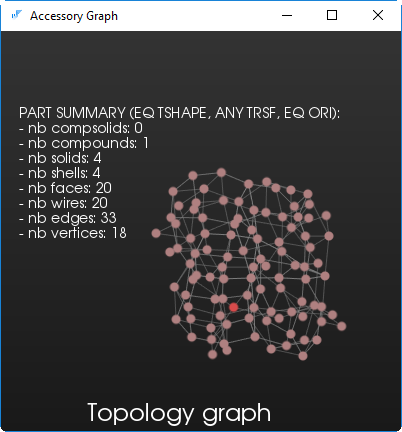
Рис. 3. Топологический граф ячеистой модели из рис. 2.
Интересно заметить (для выработки интуиции), что топологический граф немногообразной модели более «запутан» в сравнении с графом аналогичного классического представления (рис. 4). Многообразная модель визуально не отличается от ячеистой, но в реальности все ее ребра не более, чем дважды входят в грани-перегородки. Сами перегородки при этом дублируются.
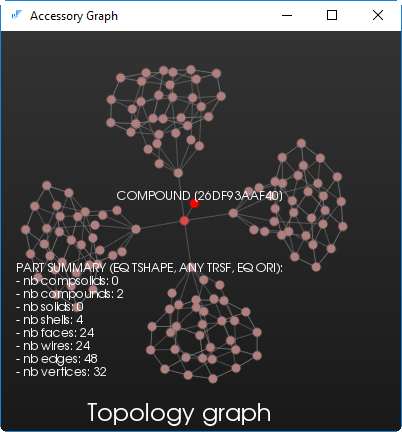
Рис. 4. Топологический граф многообразной модели с касаниями на гранях.
Немногообразность — это довольно «хрупкое» свойство. Оно легко может оказаться утраченным в результате процесса обмена данными. Скажем, если использовать умолчательный режим трансляции STEP в OpenCascade (write.step.nonmanifold = 0), то вся наша ячеистая структура будет декомпозирована на изолированные многообразные кубики. Чтобы избежать этого и сохранить результат моделирования «как есть», следует сохранить геометрию в родном формате OpenCascade — в формате BREP.
Draw> save r D:/NMSTEP/cells.brep
Немногообразия в STEP
Для представления немногообразий в STEP, библиотека OpenCascade использует объект NON_MANIFOLD_SURFACE_SHAPE_REPRESENTATION (NMSSR). Посмотрим, как будет организовано STEP-представление простого кубика (рис. 1) в многообразном и немногообразном режимах записи. Различия между двумя режимами можно наглядно показать графически, при помощи специально построенных графов отношений между STEP-объектами.
write.step.nonmanifold = 0
В этом режиме немногообразная модель будет «разорвана» на множество составляющих ее многообразий. Детальная схема результирующего представления показана на рис. 5. Обратите внимание, что в таком режиме мы имеем 12 раздельных геометрических объектов для граней (условно отмеченных на схеме как GEOMETRY). Очевидно, перегородка перестала существовать как разделяемая структура данных.
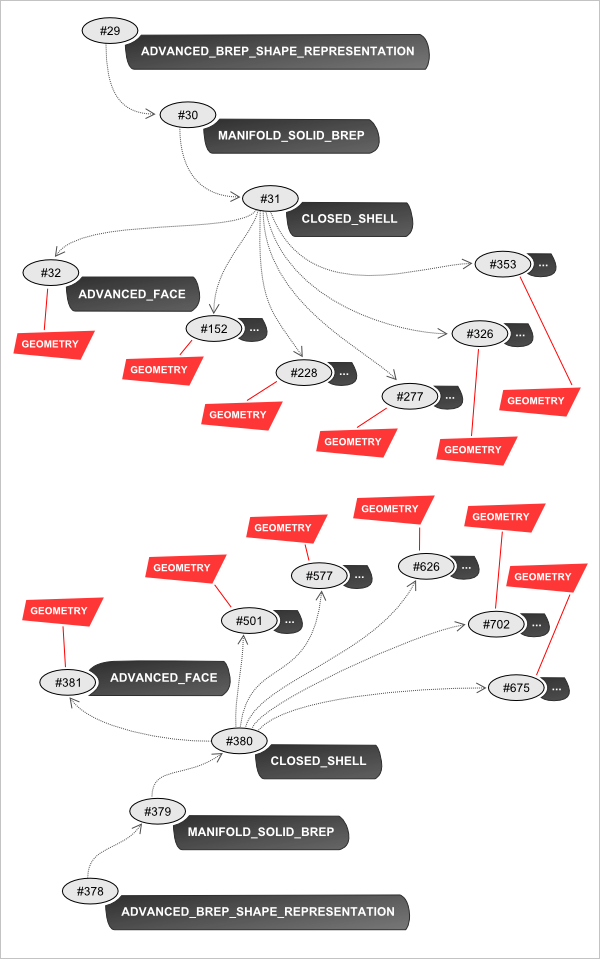
Рис. 5. Отношения между объектами в многообразном режиме.
Любопытно, что путем записи немногообразной геометрии в STEP с последующим ее прочтением оттуда, мы можем перейти к многообразному представлению. С одной стороны это потеря данных, с другой — специфический ловкий трюк.
write.step.nonmanifold = 1
Режим немногообразной записи дает другие отношения между объектами в STEP (рис. 6). Обратите внимание, что вместо двух моделей ADVANCED_BREP_SHAPE_REPRESENTATION теперь имеется единственный экземпляр NON_MANIFOLD_SURFACE_SHAPE_REPRESENTATION. Но главное, что немногообразность не была утрачена, и два вхождения типа ADVANCED_FACE теперь имеют одинаковую геометрическую подложку.
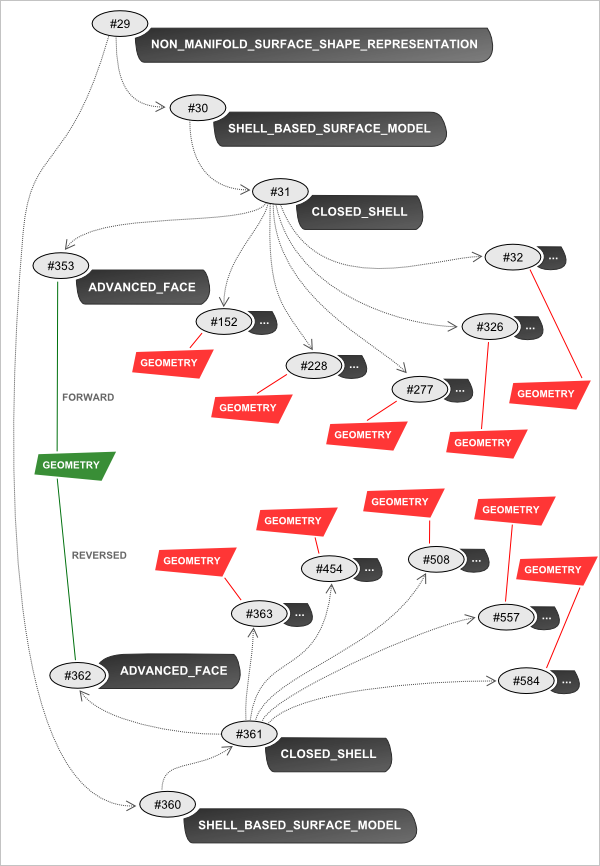
Рис. 6. Отношения между объектами в немногообразном режиме. Зеленым цветом мы промаркировали разделяемую геометрическую подложку мембраны.
Заметим, что структура наших «слипшихся» кубиков такова, что каждый из них сохраняет по 6 граней, оставаясь, сам по себе, замкнутой оболочкой. В немногообразном режиме мы имеем 12 граней типа ADVANCED_FACE и лишь 11 геометрических структур, одна из которых разделяема.