К эйлеровым операторам: топологический киллер
"As we see more emphasis being placed on direct modeling techniques in the CAD world, and extending into related applications such as model clean up for CAE analysts, the need for so called local operations is increasing in the modeler." Ken Versprille. 2013. http://isicad.net/articles.php?article_num=16045
Введение
Прямое редактирование граничной модели следует базировать на эйлеровых операторах. Как указывали известные исследователи нашей области, эйлеровы операторы чем-то смахивают на язык ассемблера для B-Rep. Их использование не только гарантирует топологическую целостность модели, но и радикально сокращает объем кода, который требуется повторять из алгоритма в алгоритм.
Под эйлеровым оператором понимается такая модификация топологии модели, которая оставляет без изменения известное соотношение Эйлера-Пуанкаре. Нередко указывается также и то, что сам оператор ничего не делает с формой изделия и служит лишь для подготовки ее топологического скелета. В терминах программирования это означает всего лишь подготовку структур данных так, чтобы они оставались в непротиворечивом, целостном состоянии. Например, удаление вершины должно сопровождаться удалением ребра, чтобы соотношение Эйлера-Пуанкаре продолжало удовлетворяться. Обычно такими общими фразами и ограничиваются, описывая идею оператора, оставляя механику его реализации на откуп конкретной системе геометрического моделирования. На самом деле, соотношение Эйлера-Пуанкаре — не единственный показатель, на который надо обращать внимание при реализации топологических операторов.
Контрольная сумма
Эйлерова характеристика по отношению к граничной модели в САПР — не более чем контрольная сумма (checksum). По сути это число, изменение которого в процессе редактирования модели сигнализирует о некорректности выполненной операции. Эйлерова характеристика есть инвариант некоторого набора топологических операторов, которые и называют эйлеровыми. Связывая количество вершин, граней, ребер, род многообразия и некоторые другие количественные характеристики модели, уравнение Эйлера-Пуанкаре остается слепым по отношению к чисто техническим деталям реализации топологии, таким как смежность граней или взаимная ориентация вложенных топологических элементов. Это очень важно, так как, скажем, наличие восьми вершин, двенадцати ребер и шести граней еще не делает объект топологически эквивалентным параллелепипеду. Количественная мера недостаточна. Чтобы судить о топологической эквивалетности двух моделей, следует сравнивать не только числа Эйлера, но и их формальные топологические графы.
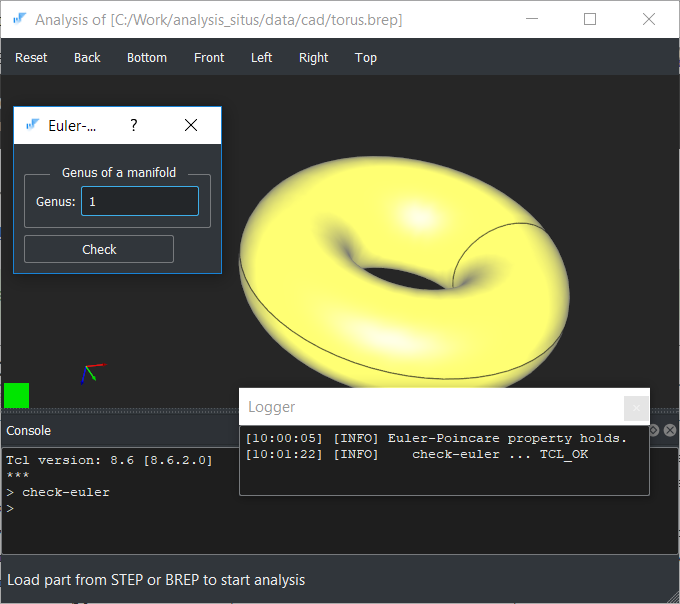
Проверка соотношения Эйлера-Пуанкаре для многообразия рода один (тор).
Топологический киллер
Как отмечают (Mantyla and Sulonen. GWB: A solid modeler with Euler operators. 1982), эйлеровы операторы неинтуитивны и не должны предоставляться пользователям САПР в качестве инструментов для редактирования геометрии. Это средство ядра, гарантирующее топологическую корректность модели в процессе модификации. Но эйлеров оператор — это еще не самый нижний уровень с точки зрения алгоритмиста. Для реализации этих операторов требуется полный контроль над топологической структурой модели, включая процедуры для работы с топологическим графом на «молекулярном уровне». Ранее мы говорили об одном инструменте библиотеки OpenCascade, позволяющем редактировать топологический граф. Не претендуя на критику, заметим лишь, что в ходе дальнейшей работы над прямым редактором B-Rep, от использования Re-Shape пришлось частично отказаться в связи с некоторыми странностями (особенностями?) его работы. Спустя время, в программе Analysis Situs появился альтернативный инструмент asiAlgo_TopoKill, спроектированный как основа для эйлеровых операторов типа K (например, KEV, KEF). Инструмент работает в двух режимах: удаление и замена на однородный элемент.
Как было указано в заметке о валидации топологических операторов, модификация элементов модели затрагивает не только целевые структуры данных, но и родительские узлы графа. Этот процесс схематично показан на картинке ниже, где целью модификации является замена вершины.
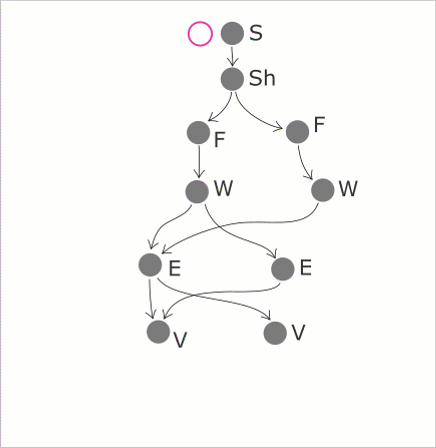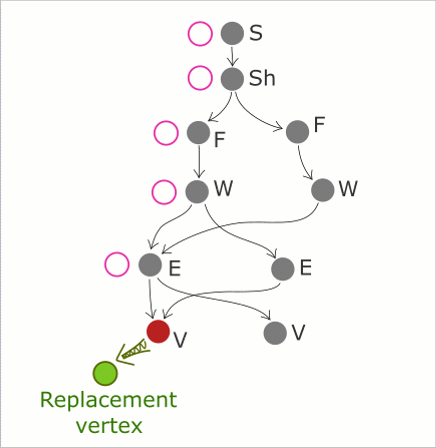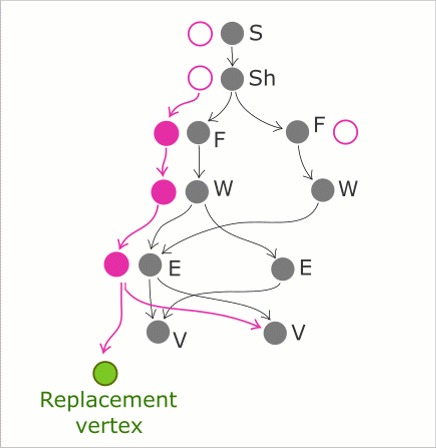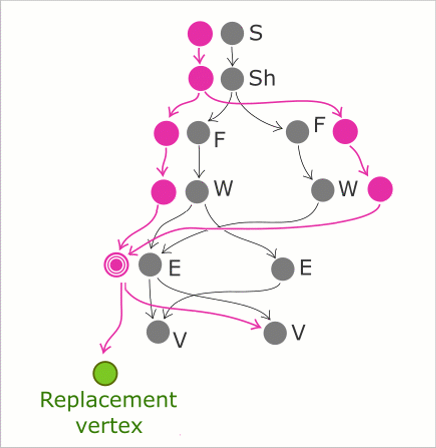
Принцип работы топологического киллера на примере замены вершины. Аналогичным образом происходит замена и удаление других типов граничных элементов.
Алгоритм итерирует топологический граф в глубину, попутно создавая новые узлы, но не соединяя их ребрами. Включение элементов друг в друга происходит «на обратном пути», когда состав обновленной модели уже определен. Незатронутые модификацией структуры данных переиспользуются, то есть оператор по существу локален.