Строим лоскут Кунса

Введение

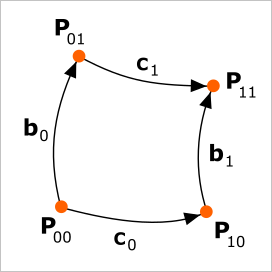Лоскут Кунса в принятых обозначениях.

Лоскуты Кунса известны в области геометрического моделирования с конца 60-х годов прошлого века [Coons, S. 1967. Surfaces for computer-aided design of space forms]. В 1983-м году Уильям Гордон дал общий математический аппарат для построения параметрических лоскутов, проходящих через заданную сетку кривых [Gordon, W. 1983. An Operator Calculus for Surface and Volume Modeling. IEEE Computer Graphics and Applications 3, 7, 18–22]. Метод Гордона, обобщающий метод Кунса, основан на понятии линейного оператора P, представляющего собой некоторую схему интерполяции. Комбинируя три линейных оператора, обладающих различными свойствами в смысле точности приближения, Гордон получает схему «трансфинитной интерполяции».

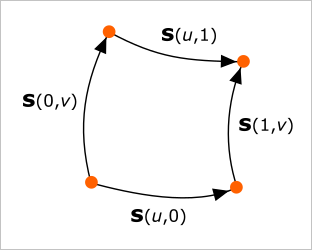Контур из четырех кривых, имеющих попарные общие точки. Если пары кривых заданы на общем базисе, то на них можно построить лоскут Кунса.

Идея метода Гордона состоит в конструировании нового оператора интерполяции путем комбинирования трех операторов P₁, P₂ и P₁₂. Каждый такой оператор, взятый в отдельности, обладает некоторым интерполяционным свойством относительно исходной сети кривых. Если же составить сумму операторов, то полученная схема интерполирует всю сеть полностью.

В англоязычной литературе эта комбинация называется булевой суммой ("Boolean sum"). Здесь оператор P₁ интерполирует кривые S(0,v) и S(1,v); оператор P₂ интерполирует противоположные кривые S(u,0) и S(u,1); оператор P₁₂ интерполирует только угловые точки. Таким образом, поверхности P₁S и P₂S являются линейчатыми, а поверхность P₁₂S есть «косая плоскость», вычитание которой компенсирует невязки интерполянтов P₁S и P₂S.

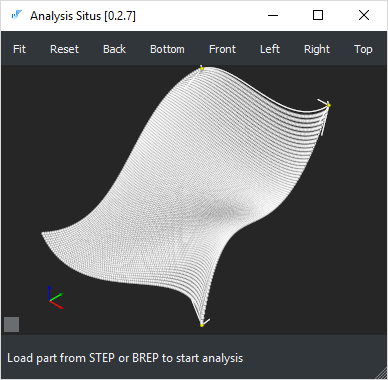Лоскут Кунса, отрисованный путем сэмплирования точек поверхности. Для его отрисовки стандартными средствами среды прототипирования требуется конвертация в NURBS.

Технически, реализация поверхности Кунса ничего не стоит. Точную формулу, описывающую лоскут Кунса по опорным кривым можно найти, например, в монографии Н.Н. Голованова «Геометрическое моделирование». Однако есть нюанс. Лоскут Кунса не является стандартным типом поверхности и для его передачи, скажем, посредством формата STEP, потребуется осуществить преобразование в более универсальный вид, такой как NURBS (B-поверхность).

Преобразование в B-поверхность

Способ преобразования лоскута Кунса в B-поверхность хорошо известен [Lin, F. and Hewitt, W.T. 1994. Expressing Coons-Gordon surfaces as NURBS. Computer-Aided Design 26, 2, 145–155]. Идея алгоритма состоит в том, чтобы построить булеву сумму, компонентами P₁S, P₂S и P₁₂S которой являются B-поверхности, определенные на едином базисе. Строго говоря, речь идет вовсе не о «преобразовании» одной формы в другую, но о построении с нуля такой B-поверхности, которая в точности совпадает с лоскутом Кунса как геометрическое место точек. Основные этапы этого процесса следующие:

1. Протянуть поверхность P₁S скиннингом через пару опорных кривых S(0,v) и S(1,v).





2. Протянуть поверхность P₂S скиннингом через пару опорных кривых S(u,0) и S(u,1).





3. Построить «косую плоскость» P₁₂S на угловых точках.





4. Привести поверхности P₁S, P₂S и P₁₂S к единому базису путем добавления недостающих узлов, повышения степени и транспонирования (если необходимо) криволинейных координат.


5. Построить новую B-поверхность путем сложения координат контрольных точек поверхностей P₁S, P₂S и вычитания координат контрольных точек P₁₂S.

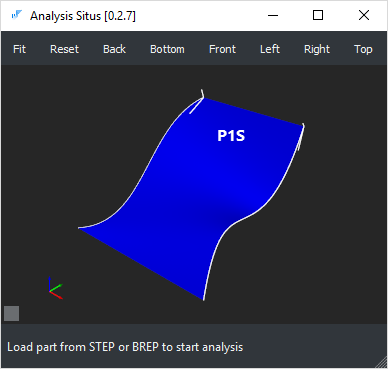
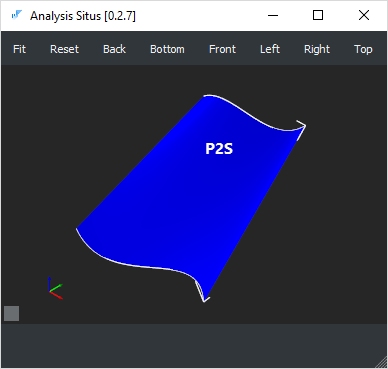
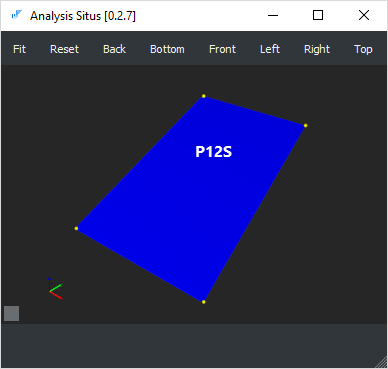
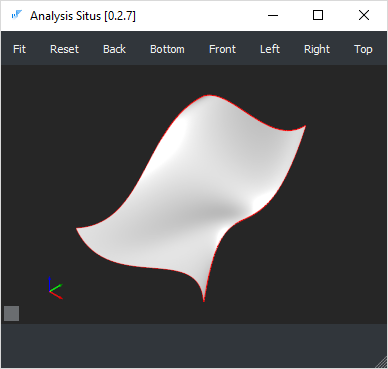Лоскут Кунса в виде B-поверхности.

Все три поверхности (P₁S, P₂S и P₁₂S) должны иметь одинаковое начало собственных криволинейных систем координат. В противном случае, результирующая поверхность не будет интерполяционной для заданных кривых.

Некоторые эксперименты

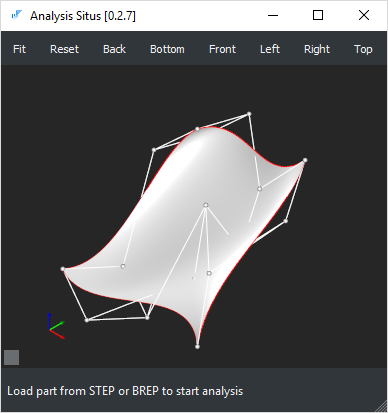
Подход, изложенный выше, был опробован на четырех скрещивающихся кривых Безье четвертого порядка (т.е. степени 3). В результате получилась поверхность Кунса в виде бикубического лоскута Безье с общим количеством контрольных точек равным 16-ти (см. команду "test-coons1" в программе Анализ Положения).

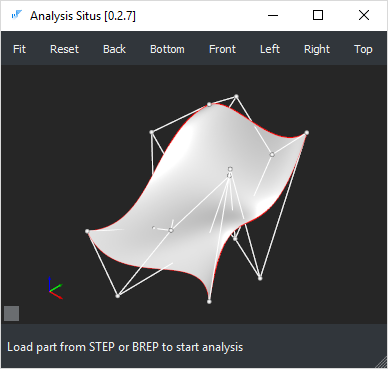Контрольные точки построенного лоскута Кунса.

Для сравнения мы взяли инструмент GeomFill_ConstrainedFilling библиотеки OpenCascade. Данный инструмент предназначен для затягивания поверхностью заданных граничных кривых. Был опробован следующий код:

bool Fill4Contour(const std::vector<Handle(Geom_BSplineCurve)>& curves,
                  Handle(Geom_BSplineSurface)&                  result)
{
  if ( curves.size() != 4 )
    return false;
  
  Handle(GeomFill_SimpleBound) b1 = new GeomFill_SimpleBound(new GeomAdaptor_HCurve(curves[0]), 1e-3, 1e-2);
  Handle(GeomFill_SimpleBound) b2 = new GeomFill_SimpleBound(new GeomAdaptor_HCurve(curves[1]), 1e-3, 1e-2);
  Handle(GeomFill_SimpleBound) b3 = new GeomFill_SimpleBound(new GeomAdaptor_HCurve(curves[2]), 1e-3, 1e-2);
  Handle(GeomFill_SimpleBound) b4 = new GeomFill_SimpleBound(new GeomAdaptor_HCurve(curves[3]), 1e-3, 1e-2);
  
  GeomFill_ConstrainedFilling filling(3, 100);
  filling.Init(b1, b2, b3, b4);
  //
  result = filling.Surface();
  return true;
}

В конструктор класса GeomFill_ConstrainedFilling подается максимальная степень базисной функции и некоторое ограничение на количество сегментов сплайна, которое мы, не особо задумываясь, выставили равным 100. В результате получилась такая поверхность:

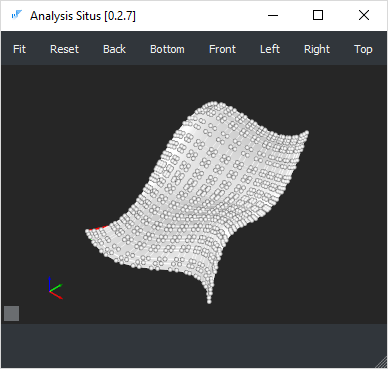Поверхность, построенная инструментом GeomFill_ConstrainedFilling на том же наборе кривых, что и лоскут Кунса, представленный выше.

Результирующая поверхность уже не является поверхностью Безье (она имеет внутренние узлы) и содержит 768 контрольных точек. Кроме того, данная поверхность не является и поверхностью Кунса, в чем можно убедиться путем ее визуального сравнения с «идеальным» просэмплированным облаком.

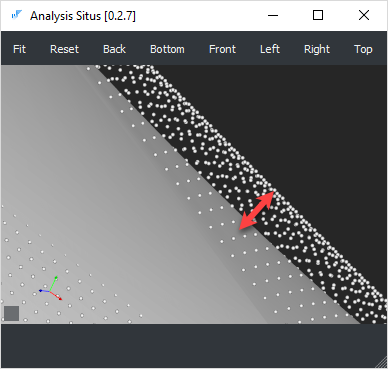Отличие поверхности, построенной инструментом GeomFill_ConstrainedFilling от поверхности Кунса.

В случае, если ограничить количество сегментов в GeomFill_ConstrainedFilling единицей, то в результате, действительно получается поверхность Безье (то есть сплайн из ровно одного сегмента).

Поверхность Безье, построенная инструментом GeomFill_ConstrainedFilling при количестве сегментов равном 1.

Однако такая поверхность вовсе не является лоскутом Кунса и не интерполирует граничные кривые.

Нарушение границ.

Заключение

Моделирование свободной формы, оно же — скульптурное моделирование или моделирование органических фигур, требует специального геометрического аппарата. Такой аппарат дают, например, поверхности подразделения (subdivision surfaces), модные и патентованные T-сплайны, а также старый добрый NURBS. Поверхность Кунса — это своеобразная точка старта для моделирования сплайнами. Ее замечательное свойство состоит в том, что данная поверхность проходит через свои опорные кривые без какой-либо алгоритмической погрешности. С другой стороны, лоскут Кунса — это лишь малая часть того геометрического арсенала, который необходим для проектирования свободной формы. В будущем мы планируем поговорить об этих вещах подробнее.