Пересечение отрезков в OpenCascade
«Вычислив по таблицам Тихо Браге сорок положений планеты, Кеплер получил кривую овальной формы и безуспешно пытался выразить ее математической формулой. Он писал, что трудность этой задачи сводит его с ума» (из статьи «Торжество предвидения», журнал Техника Молодежи — 11, 1978г.).
Будем решать простую геометрическую задачу о нахождении пересечения двух прямолинейных отрезков.
Казалось бы, чего уж проще. Однако, без геометрической библиотеки под рукой, эта задача и ей подобные могут выпить немало крови программиста. Сегодня мы будем искать решение при помощи библиотеки Open CASCADE Technology (OCCT), которая, хочется верить, избавит нас от всякого рода линейной алгебры и поможет получить результат быстро и просто.
Фундаментальные алгоритмы библиотеки Open CASCADE Technology, как геометрического ядра, сосредоточены в директориях («пакетах») GeomAPI и Geom2dAPI. Здесь вы найдете базовую функциональность для пересечения кривых и поверхностей, для проецирования точек и кривых, а также для простейшего реверсивного инжиниринга (восстановления геометрии по облаку точек). Если мы работаем в двумерном пространстве, то используется пакет Geom2dAPI. Для работы в 3D используем GeomAPI. В обоих случаях наша задача о пересечении отрезков может быть решена с использованием готовых алгоритмов OCCT. Условимся работать в 2D.
Инструмент Geom2dAPI_InterCurveCurve позволяет найти пересечение двух параметрических кривых в самом общем случае. Документация по этому классу вместе с примером его использования доступна на официальном сайте разработчиков OCCT. Сразу возникает два вопроса:
- Как представить отрезок в OCCT?
- Будет ли алгоритм «на все случаи жизни» работать достаточно эффективно с нашей примитивной геометрией? Если верить официальной документации, то этот инструмент способен работать c любыми кривыми, включая NURBS. Означает ли это, что один и тот же численный метод используется независимо от вида кривых?
Натуральным способом представления отрезка в OCCT является ограниченная по параметру прямая линия. Создать прямую линию ничего не стоит. Сначала зададим концы отрезков как точки в пространстве 2D:
gp_Pnt2d P1(-1.0, -1.0); gp_Pnt2d P2( 1.0, 1.0); gp_Pnt2d Q1(-1.0, 1.0); gp_Pnt2d Q2( 1.0, -1.0);
Теперь создадим сегменты прямых линий:
Handle(Geom2d_TrimmedCurve) L1 = GCE2d_MakeSegment(P1, P2); Handle(Geom2d_TrimmedCurve) L2 = GCE2d_MakeSegment(Q1, Q2);
Обратите внимание на то, что приведенный код минимален. Мы не сохраняем объекты класса GCE2d_MakeSegment во временные переменные, а сразу присваиваем их результирующим кривым L1 и L2. Такой «фокус» возможен благодаря тому, что класс GCE2d_MakeSegment имеет перегруженный оператор преобразования типа.
Следующий рисунок демонстрирует только что созданные сегменты. Обратите внимание на стрелочки. Они указывают направление параметризации каждого сегмента — от первой точки ко второй.
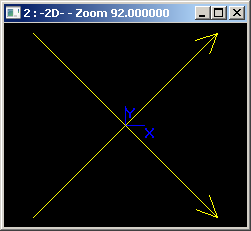
Найти пересечение теперь можно одной строчкой кода:
Geom2dAPI_InterCurveCurve IntCC(L1, L2); cout << "Number of solutions: " << IntCC.NbPoints() << endl;
Как это принято в геометрических ядрах, на простой геометрии работают специализированные алгоритмы. На сложной геометрии (Безье, NURBS, пользовательские типы) — общие алгоритмы. Пересечением конических сечений (прямых, окружностей, эллипсов, парабол и гипербол) занимается класс IntCurve_IntConicConic. Такая специализация делает алгоритм достаточно эффективным даже на больших объемах данных.
Важно также заметить, что пересечение ищется не на бесконечных прямых (хотя строгий алгебраический метод предполагает именно это), а на ограниченных сегментах. Для случая, показанного на следующей картинке, OCCT справедливо не найдет решений:
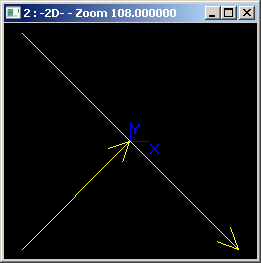
Сегменты из примера не имеют точки касания — есть небольшой зазор. Мы можем контролировать поведение алгоритма относительно допустимого зазора при помощи дополнительного аргумента, задающего погрешность:
Geom2dAPI_InterCurveCurve IntCC(L1, L2, 0.1); // Precision is 0.1 here
Понижая точность вычислений, можно добиться нахождения точки пересечения.