On geometric imprinting and debugging hints
Contour Capture
These days I was debugging an old modeling code aimed at the extraction of a piece of a two-manifold B-rep shell by a user-specified contour (Contour Capture algorithm). The code does imprinting, i.e., it geometrically and topologically fuses a contour with a shell as its first stage. The algorithms like that are pretty standard in the modeling systems. It is hard to imagine a geometric kernel that does not allow trimming shape by a loop of edges. The OpenCascade kernel is no different in this regard. It provides the so-called General Fuse operation, which can intersect topological entities with each other, and this way, prepare a model for the selection of the outcome boundaries. However, the General Fuse algorithm possesses certain deficiencies. Generally speaking, when it works, it's quite alright. But, whenever it stops working, it is a non-trivial question of how would you tune your arguments to fix the problem. This lack of control made us develop a new algorithm based on the analysis of transitions of the contour edges across the boundaries of the input shape. We named it a "Requicha's algorithm" as it is ideologically based on the work of Aristides Requicha, whose contribution to the field of geometric modeling we acknowledged here.
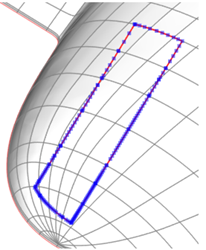 |
A sample contour to trim the model by. |
In a user interface, the engineer may specify a trimming contour as a set of points all lying on the surface with a tightest possible tolerance. These points are treated as constraints, so the output piece of the shell must contain them all. The input contour may lie at a certain distance from the shell surface. However, that distance should not go beyond a specific threshold value that allows for a robust membership classification. The algorithm attempts to survive in different edge cases where reliable classification is hard. For the sake of sustainability, it passes an alternative computational branch if the main workflow failed because of whatever reason. E.g., if the contour cannot be projected, the unprojected version is used (with a higher tolerance). Another point to keep in mind is that the input contour should not be represented as a polyline, as this adds a significant processing cost to the method. As a result, before passing the contour any further, we make sure to reapproximate it with splines.
Similarly, there are several projection tools in the algorithm's armory: normal projection and projection in the empirically defined direction. If one projection method fails, another may finish successfully. Generally speaking, the algorithm is organized into a complex computational scheme whose ingredients are made as self-robust as possible (hence the approach is entirely modular).
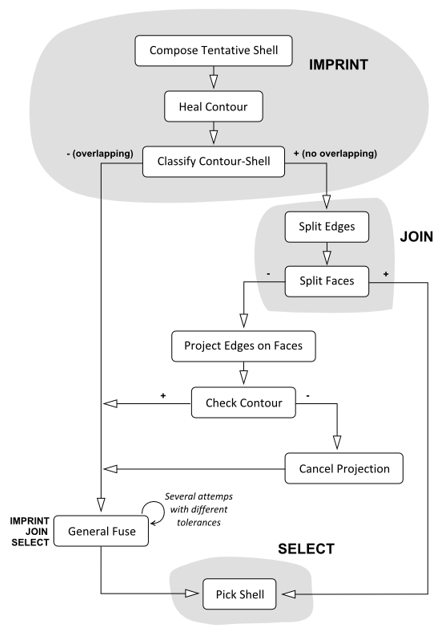 |
Algorithm's flowchart. |
The Requicha's classification is somewhat easy to implement, at least compared to the efforts required for developing a general-purpose Boolean algorithm. According to [Jackson, D.J. 1995. Boundary representation modeling with local tolerances. SMA '95: Proceedings of the Third Symposium on Solid Modeling and Applications, 247–254], the purpose of the imprinting phase is to prepare the topology. The algorithm injects the edges of a contour into the faces of a body, hence splitting them accordingly. In our realization, there are two engines for imprinting:
- Generate-and-classify algorithm as the main working branch (Requicha's algorithm);
- General Fuse (the backbone of Boolean operations in OpenCascade) for singularity cases.
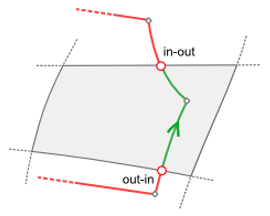 |
Classification of transitions (Requicha's algorithm). |
The generate-and-classify imprinting is based on set membership classification methods presented by Requicha and Tilove in their seminal papers [A.G. Requicha, H.B. Voelcker. Boolean Operations in Solid Modeling: Boundary Evaluation and Merging Algorithms, Technical Memorandum, January 1984] and [Tilove. Set Membership Classification: A Unified Approach to Geometric Intersection Problems // IEEE Trans. Comput. 1980. Vol. C-29, N 10. P. 874-883]. These approaches work well in the cases when the edges of the input contour do not overlap with the boundary edges of the body. The exact classification algorithms do not operate with tolerant entities. They are based on precise curve-curve intersections and do not imply computing interferences between the tolerance volumes (like in General Fuse). This peculiarity complicates the processing of overlappings, so if any singularity is detected (and cannot be escaped), the General Fuse algorithm runs as a fallback solution.
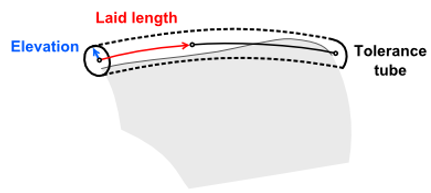 |
To the detection of overlappings: the overlapping is entirely within a tolerance tube. |
General Fuse does not operate as a primary tool because it offers less control over precision and tolerance values. While Requicha's algorithm depends mostly on the curve-curve intersection in 3D (extrema), General Fuse does a much more intensive job and works with precision values, which are not easy to calibrate.
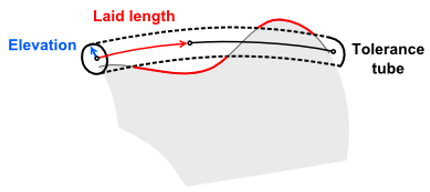 |
To the detection of overlappings: the overlapping is partly outside of a tolerance tube. |
When two curves overlap, they are not in "general position," and the typical intersection algorithms are no longer applicable. However, without overlappings handling, the imprinting algorithm is not practical. In many cases, the engineers would prefer selecting the contour lines along the features lines (i.e., the edges) of a model because the as-designed edges are natural shape delimiters. A singularity-escaping Requicha's method needs to be adjusted to treat overlappings gracefully. It is the job of Requicha's classification to detect overlappings and assess the tolerances to be passed to the General Fuse algorithm.
 |
To the detection of overlappings: two parameters defining the overlapping zone are derived from the discretized curves. |
Debugging
You might wonder how complicated that entire thing is. The worst aspect of any geometric algorithm is that it is never perfect. Depending on the quality of the argument shapes and their respective positions, one may always find a problematic configuration. Therefore, the developer of a modeling algorithm should anticipate the inevitable maintenance phase and think carefully about how to debug his stuff (given that after several months passed, he unlikely recalls much of the implementation details). Fortunately, good enough IDEs allow for many tricks that might save you a significant amount of time and brainpower if appropriately used. One such tip is documented in the OpenCascade's official docs, but it is not easy to find this pearl among the rest of the text. The idea is to use the Command Window when the application hits a breakpoint somewhere in your code.
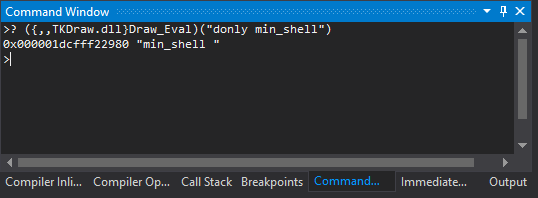 |
Debugging terminal in MS Visual Studio 2013. |
The following example asks the Draw viewer to show a specific object alone in the scene:
>? ({,,TKDraw.dll}Draw_Eval)("donly min_shell")
You may also dump your shape to the filesystem for additional checks:
>? ({,,TKBRep.dll}BRepTools_Write)("C:/users/ssv/desktop/F.brep",(void*)&F)
Notice that to invoke the functions like mentioned above, you need to know their corresponding dynamic libraries (TKDraw.dll and TKBRep.dll in our example) and their signatures. This technique is entirely complementary with the imperative plotting paradigm as it allows you to change your 3D scene (populated imperatively) as long as you debug.
 |
Use of Command Window for debugging. |
Another useful practice is to have some diagnostic outputs (both graphical and textual) in your code. You can enable them with preprocessor macro as the following snippet shows:
#define DRAW_DEBUG
#if defined DRAW_DEBUG
#pragma message("===== warning: DRAW_DEBUG is enabled")
#pragma comment(lib, "TKDraw.lib")
#endif
...
#if defined DRAW_DEBUG
// Do your dump here.
Draw::Set(...);
#endif
Thanks to the pragma message, the enabled diagnostics macro will not remain unnoticed at compilation time (if you keep your code warning-free, of course).
Conclusion
The engine of Boolean operations is a powerful thing. Many modeling algorithms can benefit from its robust core for boundary evaluation and merging. However, sometimes you need more control, or, in certain circumstances, you might be willing to take advantage of the peculiar properties of your domain (like we did in our BRS algorithm). Also, no algorithm is 100% robust, so having a fallback solution is always a strong architectural decision. With our Requicha's classifier, we solve the problem of better control over the modeling parameters and enable better overall robustness of the entire imprinting algorithm. There might also be undiscovered potential in improving the classifier's efficiency compared to the General Fuse algorithm, so there's undoubtedly something to analyze deeper.
Read also on Medium.com.
Want to discuss this? Jump in to our forum.