On recognizing canonical surfaces: cylinders
«То, что видно как фигура, нельзя оспорить или понять неправильно: вот круг, он не может совпасть с квадратом и не может с треугольником. Это и есть — Мир...» Беркем аль Атоми, «Шизофреническое (Друг мой Сашка)»
In the previous article, we emphasized the importance of modeling with clean and concise 3D primitives. To put it short, prefer analytical shapes whenever possible if you are going to recognize any features or pass your shape through the direct editing algorithms, such as push/pull.
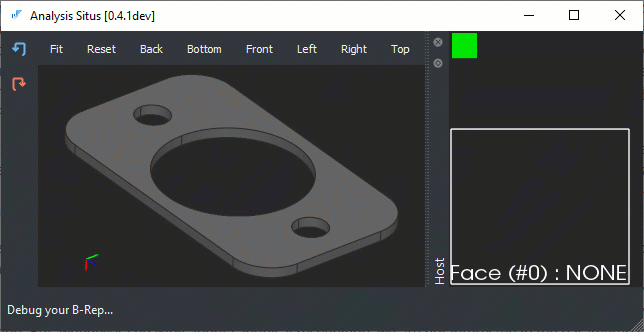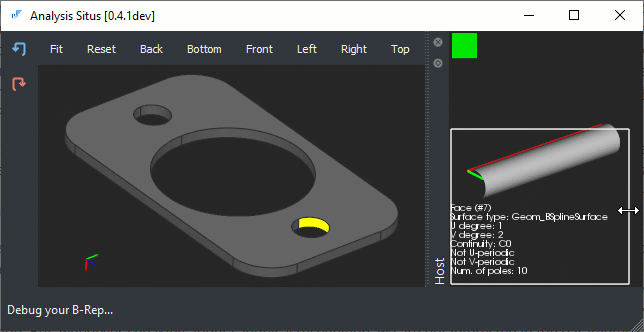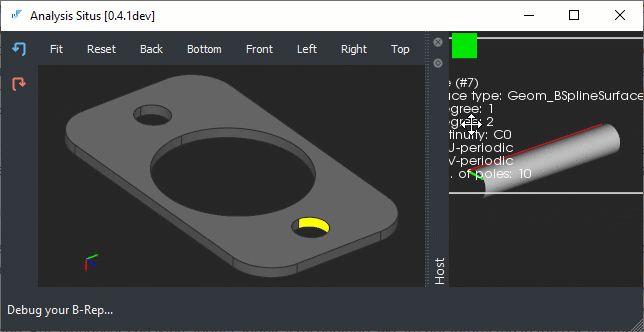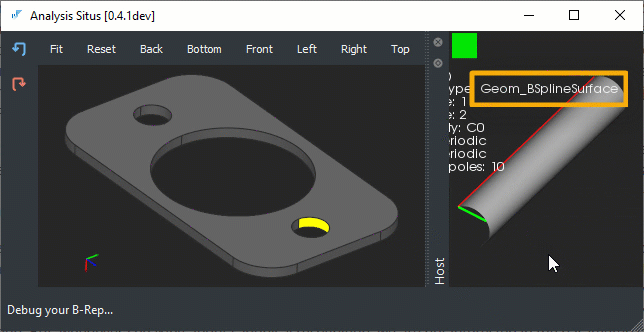 |
Non-analytical surface types for the drilled holes. |
Too often though, we have to deal with someone else's data that's composed of all sorts of excessive splines. To give such models a new breath of life, the analytical geometries should be recovered back from their freeform counterparts. It is generally wise to give analytical recognition a shot whenever you're scanning your model for features. Let's see today how to recognize the props of cylinders out of parametric surfaces defined on a UV rectangle.
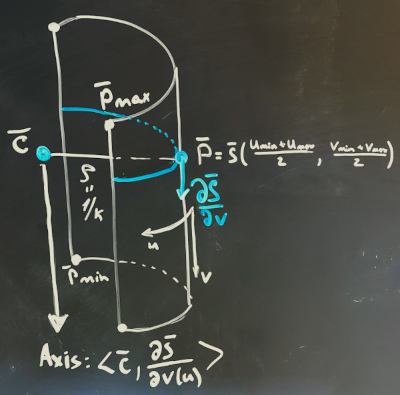 |
Curvature analysis to extract the axis. |
To start off, we need to be sure that the surface in question is of a cylindrical shape. Such analysis can be done in a pretty straightforward way. Let's probe our surface with a grid of points and measure the principal curvatures in each sample. We obtain two arrays of curvature values. One array should contain all zeroes, while another will bring us the reciprocal values for the curvature radii. The direction of zero curvature is presumably the longitudinal direction of our cylinder, so we declare it a V-direction following the convention of OpenCascade. The props we have to extract are listed below:
- Radius.
- Axis composed of the position coordinates and direction vector.
- Min and max UV bounds in the parametric space. The V-range gives us the geometric height of the cylinder. One may argue that a cylinder is an infinite surface, but since we are converting a limited potion of spline, why not map the trimming rectangle as well?
The following code can be used to evaluate the curvature of a surface at a point (check out the previous post for more details):
bool EvaluateCurvature(const Handle(Geom_Surface)& surf,
const double angleRad,
const gp_Pnt2d& UV,
double& k)
{
// Calculate differential properties.
GeomLProp_SLProps Props(surf, UV.X(), UV.Y(), 2, 1e-7);
//
if ( !Props.IsCurvatureDefined() )
{
std::cout << "Error: curvature is not defined" << std::endl;
return false;
}
// Get differential properties.
const gp_Vec Xu = Props.D1U();
const gp_Vec Xv = Props.D1V();
const gp_Vec Xuu = Props.D2U();
const gp_Vec Xuv = Props.DUV();
const gp_Vec Xvv = Props.D2V();
const gp_Vec n = Props.Normal();
// Coefficients of the FFF.
const double E = Xu.Dot(Xu);
const double F = Xu.Dot(Xv);
const double G = Xv.Dot(Xv);
// Coefficients of the SFF.
const double L = n.Dot(Xuu);
const double M = n.Dot(Xuv);
const double N = n.Dot(Xvv);
// Calculate curvature using the coefficients of both fundamental forms.
if ( Abs(angleRad - M_PI*0.5) < 1.0e-5 )
{
k = N / G;
}
else
{
const double lambda = Tan(angleRad);
k = (L + 2*M*lambda + N*lambda*lambda) / (E + 2*F*lambda + G*lambda*lambda);
}
return true;
}
The function accepts the angle in the UV space that determines the direction of the corresponding CONS (Curve ON Surface). Another input is the UV coordinates of the probe point itself. To get the curvature values along the isoparametric lines, one should call this function twice, passing zero and PI/2 values for the inclination angle subsequently. Here we go:
EvaluateCurvature(surface, 0., uv, k0); EvaluateCurvature(surface, M_PI/2., uv, k1);
To extract the cylinder axis, we can take the osculating circle's center constructed for the curved isoline. The axis' direction is given by the corresponding partial derivative.
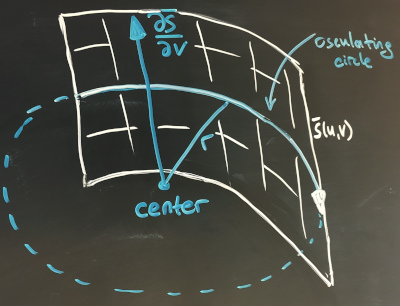 |
The osculating circle to recover the cylinder axis. |
Analytical recognition is the essential ingredient of any feature recognition SDK. It brings a couple of functions that you'd normally expect to see in conjunction: the recognition itself, and the conversion. At the same time, no real modification has to necessarily happen as feature recognition is apparently a read-only business. Still, analytical recognition is a "shape healing" operator aimed to prepare your model for further processing, no matter which. We will return to that topic in one of our future articles. Watch your shape.
Want to discuss this? Jump in to our forum.