Поверхность Безье на семействе кривых
Сегодня мы поговорим о параметрических поверхностях довольно хитрого вида. Это поверхности, которые задаются рациональной формулой Безье на опорных кривых. Интересуют они нас постольку, поскольку такие поверхности могут использоваться для построения гладких сопряжений между гранями CAD-модели.
Ну вот, математика...
Для начала немного математики. Рациональная поверхность Безье, построенная на семействе кривых в общем виде задается формулой:
\begin{equation*} S(u, v) = \frac{\sum_{i=0}^n B_i^n(v) w_i(u) c_i(u)}{\sum_{i=0}^n B_i^n(v) w_i(u)} \end{equation*}
Здесь
- $B_i^n(v)$ — базисные полиномы Бернштейна;
- $w_i(u)$ — весовая функция, принимающая любые значения на числовой оси;
- $c_i(u)$ — параметрические кривые семейства.
Будем верить, что приведенная формула действительно описывает гладкую ориенируемую поверхность, хотя, сторого говоря, это необходимо доказать. Как минимум, очевидно, что приведенная формула задает некоторую векторную функцию, ставящую в соответствие точкам $(u,v) \in R^2$ точки $(x,y,z) \in R^3$.
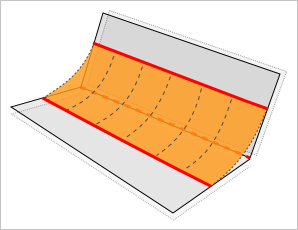
Теперь от общей формулы перейдем к ее частному случаю, когда в наличии имеется семейство из 3-х кривых. Рассмотрим кривые $r(t)$, $q(t)$ и $c(t)$. Договоримся называть кривые $r(t)$ и $q(t)$ опорными, а кривую $c(t)$ — центральной. Также условимся, что весовая функция отлична от нуля только для центральной кривой. Тогда для случая трех кривых наша формула может быть переписана в виде:
\begin{equation*} S(u, v) = \frac{B_0^2(v) r(u) + B_1^2(v) w(u) c(u) + B_2^2(v) q(u)}{B_0^2(v) + B_1^2(v) w(u) + B_2^2(v)} \end{equation*}
Базисные функции Бернштейна имеют следующий вид:
\begin{equation*} B_i^k(v) = C_i^k v^i (1 - v)^{k-i} \end{equation*}
Здесь
- $k$ — степень базисных функций;
- $C_i^k$ — биномиальный коэффициент.
Явно раскрывая выражения для базисных функций Бернштейна, имеем:
\begin{equation*} S(u, v) = \frac{(1-v)^2 r(u) + 2v(1-v) w(u) c(u) + v^2 q(u)}{(1-v)^2 + 2v(1-v) w(u) + v^2} \end{equation*}
Обратите внимание, что мы используем один и тот же параметр $u$ как для кривых $r(u)$, $c(u)$ и $q(u)$, так и для весовой функции $w(u)$. Это важное ограничение, предполагающее, что все кривые параметризованы на одном и том же интервале $u \in [a;b]$. Более того, если мы хотим получить «хорошую» поверхность, разумно потребовать и некоторой синхронности их параметризации. Пример квазисинхронной параметризации дает следующий рисунок:
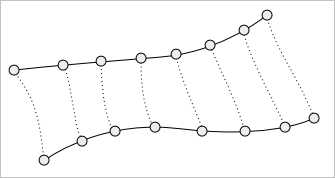
Здесь для каждого фиксированного значения параметра $u$ все кривые «успевают пробежать» почти (отсюда и приставка «квази») одинаковые расстояния. Пример же «плохой», асинхронной параметризации иллюстрирует рисунок ниже:
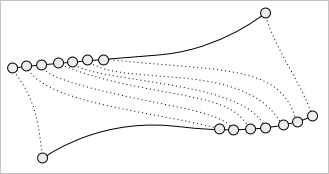
В принципе обе приведенные поверхности являются геометрически корректными. Однако всякого рода алгоритмы, которые вы захотите к ним применить, будут, скорее всего, работать по-разному. Например, результат алгоритма триангуляции так или иначе будет зависеть от параметризации исходной поверхности. В примере выше «плохая» поверхность едва ли может быть покрыта регулярной сеткой без дополнительных ухищрений. Распознать проблемы подобного рода можно взглянув на плотность изопараметрических линий вашей поверхности ($u = const$ и $v = const$). В идеальном случае они не должны иметь неоправданных сгущений.
Но вернемся к нашей формуле для поверхности $S(u,v)$ в случае трех кривых. Нетрудно видеть, что при $v = 0$ поверхность $S(u, 0)$ представляет собой кривую $r(u)$. Аналогично, при $v = 1$ поверхность вырождается в кривую $q(u)$. Это означает, что поверхность $S(u, v)$ проходит через кривые $r(u)$ и $q(u)$.
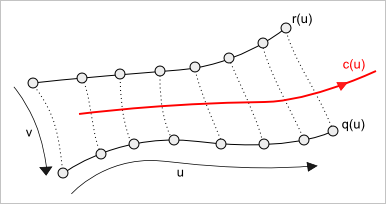
Остается выяснить поведение нашей поверхности по отношению к центральной кривой $c(u)$. Но хватит математики. Для большего удовольствия перейдем сразу к численным экспериментам.
Полевые испытания
Несмотря на то, что формула $S(u, v)$ довольно проста, имеется «небольшой нюанс», усложняющий сиюминутное тестирование. Дело в том, что мы ни слова не сказали о том, какова природа семейства кривых $r(u)$, $q(u)$ и $c(u)$. Единственное ограничение, которое было указано выше — требование согласованности их параметризаций. На практике эти кривые могут быть чем угодно (самый общий случай — NURBS-представление). Таким образом наше желание «поиграться» с поверхностью Безье вскрывает необходимость иметь технические средства для представления параметрических кривых. Неплохой вариант в такой ситуации — использовать библиотеку Open CASCADE Technology, где реализовано множество разновидностей пространственных кривых.
О том, как использовать Open CASCADE Technology для моделирования пользовательских типов поверхностей мы поговорим в другой раз. Сегодня же позвольте мне воспользоваться библиотекой Quaoar для проведения численных экспериментов.
Для начала выберем опорные кривые семейства. Я намеренно использовал B-кривые разных степеней, чтобы показать, что полная согласованность семейства некритична (хотя и желательна).
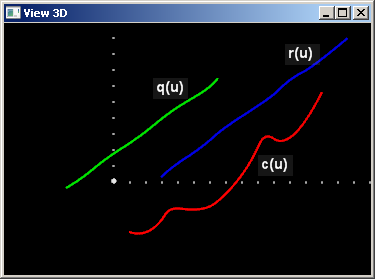
Теперь разберемся с весовой функцией $w(u)$, которая, как мы помним, является множителем средней кривой $c(u)$. Нетрудно видеть, что чем больше значения $w(u)$, тем существенней вклад кривой $c(u)$ в формуле для поверхности $S(u,v)$. Напротив, если вес $w(u)$ всюду равен нулю, то кривая $c(u)$ перестает оказывать какое-либо воздействие на итоговую поверхность. Посмотрим, как такая зависимость выглядит геометрически.
Зафиксируем значение веса $w(u) \equiv 1$. Результирующая поверхность принимает следующий вид:
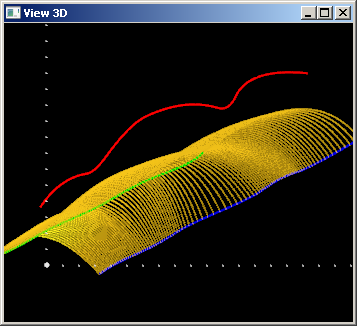
Мы видим, что поверхность притягивается к центральной кривой, но не проходит через нее. Увеличим значение веса. Пусть $w(u) \equiv 20$:
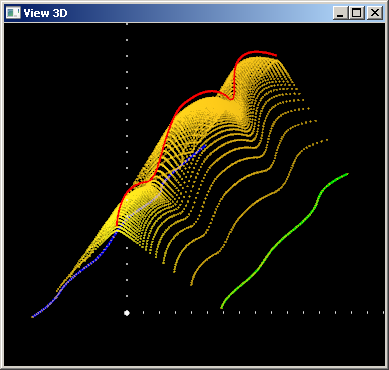
Тенденция ясна: чем больше значение веса, тем ближе поверхность проходит к центральной кривой. Из формулы для $S(u,v)$ хорошо видно, что поверхность пройдет в точности через центральную кривую в случае, если $w(u) \equiv \infty$.
Проверим, как поведет себя поверхность в случае $w(u) \equiv 0$:
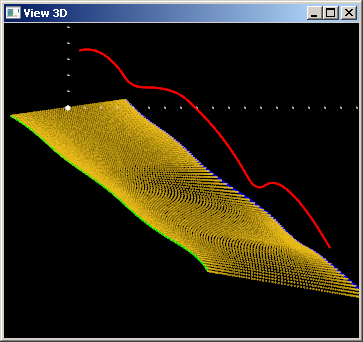
Кривая $c(u)$ больше не участвует в формообразовании поверхности. Это, однако, не означает, что поверхность вырождается в плоскость, так как кривые $r(u)$ и $q(u)$ не обязаны быть планарными:
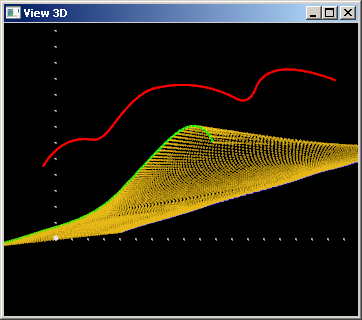
Наконец, интересен вариант с отрицательным весом. Зафиксируем $w(u) \equiv -0.5$:
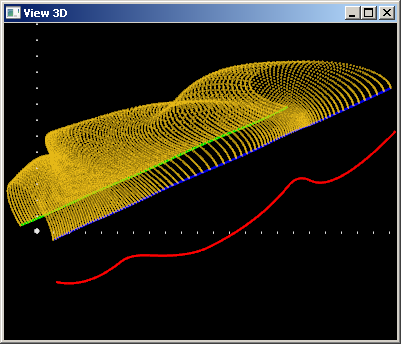
Из рисунка видно, что в случае отрицательного веса центральная кривая «отталкивает» поверхность. Однако здесь внимательный читатель вполне может возмутиться и поймать меня за рукав. Да, отрицательное значение я выбрал довольно скромное (-0.5). Но почему?
Что, опять математика?
Совсем чуть-чуть. Рациональная формула для поверхности $S(u,v)$ таит в себе подводный камень, связанный с возможным делением на ноль. Нетрудно видеть, что с точки зрения весовой функции, таковое деление произойдет в случае, если выполнится следующее равенство:
\begin{equation*} w(u) = -\frac{v^2 + (1-v)^2}{2v(1-v)} \end{equation*}
По определению параметр $v$ принадлежит отрезку $[0;1]$, и мы достоверно знаем, что при $v = 0$ и $v = 1$ поверхность пройдет через опорные кривые $r(u)$ и $q(u)$. Для всех прочих значений выражение, приведенное выше, всегда отрицательное. Этот факт заставляет насторожиться. Получается, что некоторый отрицательный вес вполне может удовлетворить приведенному равенству. Далеко за примером ходить не надо. Пусть $w(u) \equiv -1$. Из равенства имеем:
\begin{equation*} (2v - 1)^2 = 0 \end{equation*}
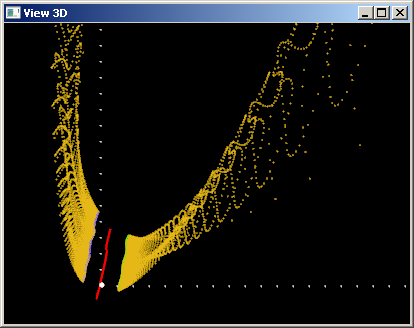
Следовательно, при значениях $v = 0.5$ знаменатель выражения для поверхности $S(u,v)$ обращается в ноль. Числитель же такой склонности не демонстрирует. Таким образом вектор-функции $r(u)$, $c(u)$ и $q(u)$ домножаются на бесконечно большое число, в результате чего наша поверхность «разрывается» в бесконечность. Выглядит это очень неприятно:
Приведенное равенство можно изобразить графически:
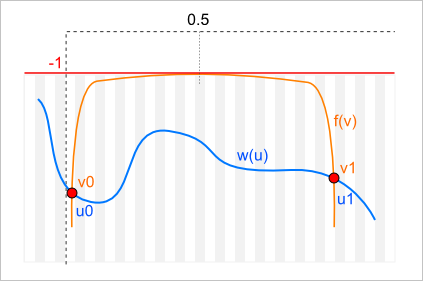
Здесь
\begin{equation*} f(v) = -\frac{v^2 + (1-v)^2}{2v(1-v)} \end{equation*}
Пересечение двух графиков возможно только в том случае, если весовая функция проходит в области $w \le -1$. Причем таковое пересечение произойдет неизбежно, если в начальной и конечной точках кривой $c(u)$ вес не выбран бесконечным (что, как вы понимаете, едва ли имеет смысл). Так как фукции $w(u)$ и $f(v)$ — это функции разных аргументов, то искомое пересечение произойдет для некоторой пары $(u_0, v_0)$. Геометрически это означает, что поверхность $S(u,v)$ имеет особую точку с криволинейными координатами $(u_0, v_0)$. В этой точке она терпит разрыв второго рода (бесконечная величина), а потому становится непригодной для геометрического моделирования.
Закругляемся
Как было отмечено в самом начале, поверхность Безье на семействе кривых может использоваться для построения гладких сопряжений между гранями топологических объектов. Действительно, мы научились контролировать кривизну нашей поверхности, изменяя ее сопряженный вес вдоль центральной кривой. При некоторых значениях весовой функции результирующая поверхность может представлять собой след качения шара. Более того, технически нет никаких препятствий смоделировать качение шара переменного радиуса. Но об этом мы поговорим в другой раз.