True Shape Nesting 03: picking and moving a polygon

There is one reason why it makes sense to mess around with nesting in the Mobius codebase. Although this library remains pretty basic in its scripting, visualization, and algorithmic abilities (way more primitive than Analysis Situs), it allows us to build things ground-up, not respecting someone else's architecture (even if this "someone" is me). For example, adding new visualization features in Analysis Situs (based on VTK) is quite an exercise in its architecture. If I want to pick a polygon and move it around, I will be using lots of callbacks, sources, and widgets to get the job done, and it's all fine. But after more than 10 years dealing with this exact architecture (originally invented for FEA pre-/post-processors), it feels like it's sort of giving nothing back. And that's no fun.

Now let's digress from nesting and talk a bit about graphics that I think is missing to get the job done. After all, geometric computing without graphics is like flying with a pack of Belomor cigarettes as a map.

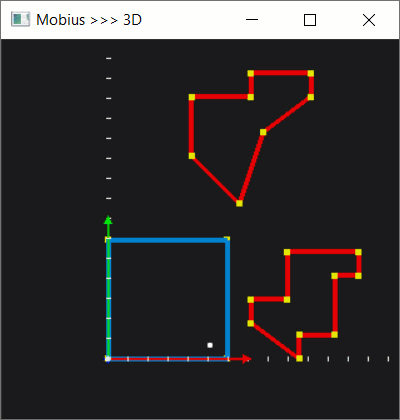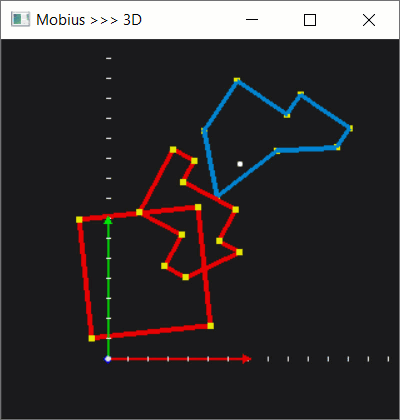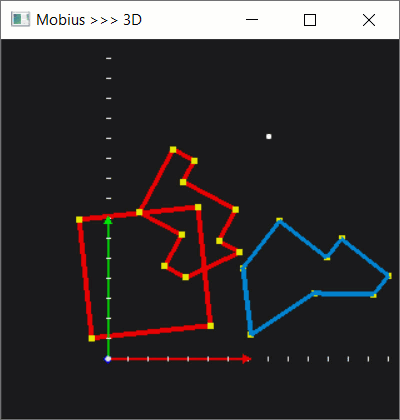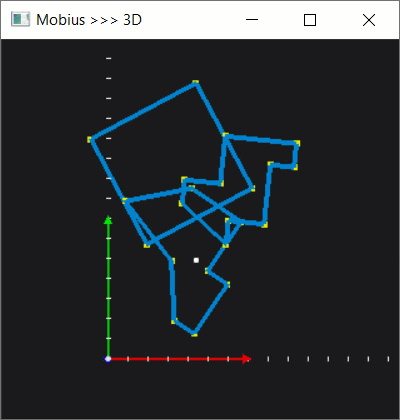
Let's add a couple of polygons to the scene using the make-polygon command introduced in the previous blog. The -close flag tells Mobius that you let it close your polygon by repeating the start point as the end one.

make-polygon a 0 0 1 0 1 1 0 1 -close
make-polygon b 1.1 1.3 1.3 1.9 1.7 2.2 1.7 2.4 1.2 2.4 1.2 2.2 0.7 2.2 0.7 1.7 -close
make-polygon c 1.2 0.3 1.6 0.0 1.6 0.2 1.9 0.2 1.9 0.7 2.1 0.7 2.1 0.9 1.5 0.9 1.5 0.5 1.2 0.5 -close
fit

Here's the corresponding scene:

With these visuals, it is already possible to perform intersection tests on the constructed polygons, but let's make it more powerful for the sake of better testability. First off, we added a function to select a polygon based on the algorithm by Eric Haines. The algorithm is nothing new: it shoots a ray from a picked point in arbitrary directions and checks if the number of intersection points is odd (point is inside) or even (point is outside). This technique of ray casting is applicable not only for polygons but for any Jordan curves. Also, the algorithm should potentially be enhanced with some extra treatment to escape from "singularities" at poles, where odds become evens or vice versa due to the lack of precision.

Then, let's make this whole business a little more interactive. Once a polygon is selected, we can let the user move it around by pressing keyboard arrows.

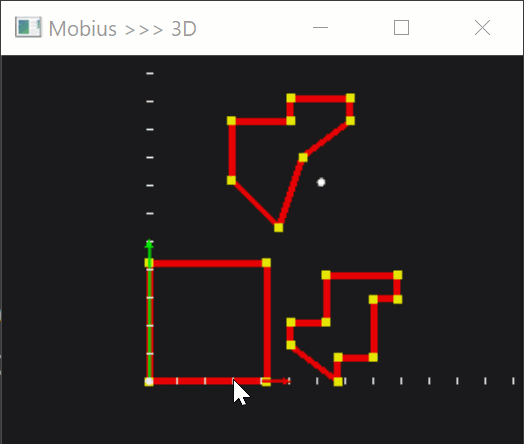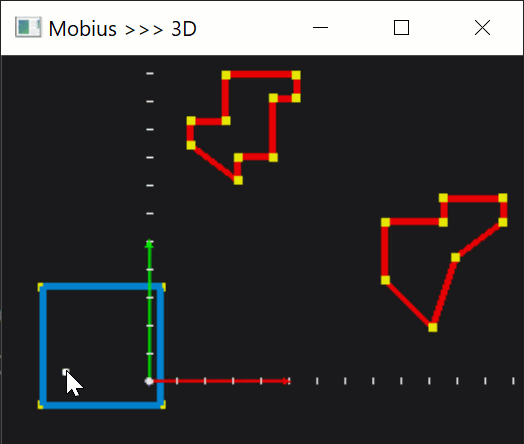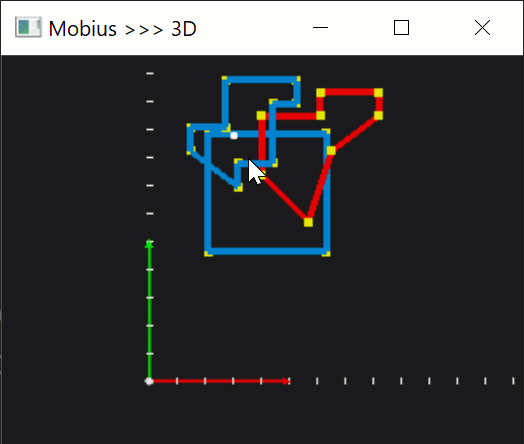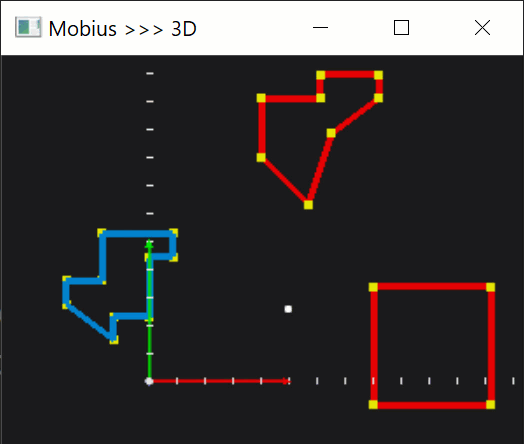With quite a standard manipulation with translation and rotation matrices, we can enable more DOFs, which would help us later on during testing.

The next step is to try to intersect a couple of polygons to see how precise, efficient, and robust our intersection tool is going to be.

Want to discuss this? Jump in to our forum.