Google Summer of Code at OPEN CASCADE
 |
Have you ever drunk cognac from a Klein bottle? Well, nevermind. |
This year, OPEN CASCADE (the company) is going to participate in the Google Summer of Code. I've never been there in any role, but the chances are we could have some fun this summer. Taking advantage of this post, I'd like to do a couple of things:
- Invite interested students to participate in the event, if OCC gets accepted by Google. You can find the list of possible projects here. Once/if the application is opened, I'll let you know with a dedicated post.
- Since I took part in preparing the project ideas, let me elaborate on some of them. This post then contributes to the series of articles that could be united under the "future of FOSS modeling" title. See other notes here and here (both are in Russian). A couple of things on push/pull were also published here.
GSoC is a nice opportunity to get started with any challenging problem. At the same time, the algorithms listed below are quite ambitious for a much longer run. The good point is that GSoC assumes mentoring, so every youngling will get his Jedi sensei for the accelerated introduction.
Regularization of B-spline objects
Regularization aims at improving the parameter flows over the B-spline curves and surfaces while not affecting their shapes. The regularization algorithm can be used as a post-processing stage in the interpolation and approximation operators, such as surface skinning, sweeping, constraint filling, and others. The algorithm makes geometry more analytically fair by moving the existing control points in tangential directions. The obtained more regular parameterization is a valuable property for subsequent numerical algorithms. The most notable application for this algorithm is the preparation of CAD geometries to quality meshing, e.g., for the sake of consequent finite element analysis. Since even the commercial-grade mesh generators are sensitive to parameterization, expressing the geometry more regularly is a relevant industrial problem.
The following animation showcases a study from the digital medicine field. The study aimed to accurately skin a surface that fits into the scan data of a human limb. The ultimate goal is to shape the inner surface of a prosthesis, i.e., the thing that's called a "socket." The wavy isoparametric lines you'd see at the end of the animation are somewhat we'd like to improve. Since we model for accuracy, such improvement should by no means modify the socket's shape. That latter requirement makes regularization different from "smoothing," which is a problem that has been already solved in the open-source community.
 |
Skinning a surface from scan data. Regularization might improve the isoparametric lines' flow. |
References
- Xu, G., & Bajaj, C. (2011). Regularization of B-Spline Objects. Computer-Aided Geometric Design, 28(1), 38–49. https://doi.org/10.1016/j.cagd.2010.09.008 (full-text link)
Push/pull editing
There are no open-source 3D graphics engines that allow for “direct modeling” of engineering and art objects in a CAD-compatible way. This project is aimed to ground a new modeling paradigm on the top of the OpenCascade library by introducing a push/pull operator. Using push/pull functions and alike, a user of an interactive system can create and edit shapes by dragging and tweaking the selected faces in a way that preserves the initial (or automatically guessed) design intent.
Various modes of the push/pull operator can be studied in the course of this project. Dragging a face may lead to different results as illustrated by the following picture (only two options are shown). Ideally, the result of dragging should preserve the original design intent of a model, although the choice of the preferred mode is normally left to the user.
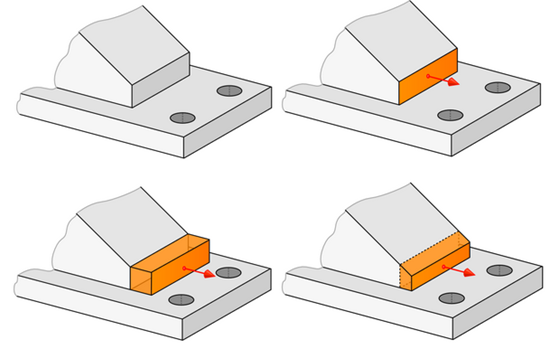 |
Push/pull modes. |
Push/pull is a pretty darn cool thing. It is also a very efficient way of introducing model changes if accompanied by other direct methods, such as simplification, changing fillets' radii, drilling holes, and many others. Basically, just open up SpaceClaim and play on there for ten minutes to see what I mean. The open-source CAD community needs that thing.
References
- Zou, Q., & Feng, H. Y. (2019). Push-pull direct modeling of solid CAD models. Advances in Engineering Software, 127 (November 2018), 59–69. https://doi.org/10.1016/j.advengsoft.2018.10.003 (full-text link)
A two-dimensional geometric constraint solver
This project aims at developing an algorithm for solving a set of algebraic equations that describe a two-dimensional sketch. Sketching a planar contour is the first stage of 3D modeling, both direct and history-based. The CAD systems’ interactive UIs are backed by two-dimensional constraint solvers that compute the involved geometric primitives' parameters, such as end positions for lines and radii of circles. Seemingly simple, constraint solving is a challenging task. Although there are several open-source solutions for that problem, none can easily be integrated with the open-source OpenCascade library.
References
- SolveSpace -- Parametric 2d/3d CAD. URL: https://solvespace.com/index.pl
- PlaneGCS solver of FreeCAD. URL: https://github.com/FreeCAD/FreeCAD/tree/master/src/Mod/Sketcher/App/planegcs
Gordon surface
This project aims at adding a new algorithm for modeling Gordon surfaces to the open-source OpenCascade library. The Gordon surface is a generalization of a well-known Coons patch to the network of curves. This type of geometry is highly demanded in digital sculpting and industrial modeling, such as designing ship hulls or pieces of aircraft fuselages. While the Gordon surface is yet another primitive type conceptually, it is nicely compatible with the standard B-spline representations. Therefore, the algorithm might construct a traditional B-spline surface that is point-to-point equal to the original shape in the Gordon form.
References
- Lin, F., & Hewitt, W. T. (1994). Expressing Coons-Gordon surfaces as NURBS. Computer-Aided Design, 26(2), 145–155. https://doi.org/10.1016/0010-4485(94)90035-3
- Siggel, M., Kleinert, J., Stollenwerk, T., & Maierl, R. (2019). TiGL: An Open Source Computational Geometry Library for Parametric Aircraft Design. Mathematics in Computer Science, 13(3), 367–389. https://doi.org/10.1007/s11786-019-00401-y
- Ayam. URL: http://ayam.sourceforge.net/features.html
- An example of a Gordon Surface, based upon OCC. URL: https://forum.freecadweb.org/viewtopic.php?f=8&t=29632&sid=9826884d01d60ac826158ae774086c85
Point inversion study
Although point inversion and projection are considered the solved problems in Computer-Aided Design and specifically in OpenCascade, there is still a direction for new exciting discoveries. A typical inversion algorithm based on Newton iterations assumes that the point to project is substantially close to the target surface. Therefore, a traditional test for point inversion consists of projecting a surface’s control poles onto itself. At the same time, there is a demand for an algorithm capable of projecting distant points with a certain level of predictability. This project aims to prototype an inversion algorithm based on state-of-the-art papers and conduct a comparative study over the existing solutions. The target geometry type is a spline curve or surface whose evaluations are computationally non-trivial. The main focus of the algorithm is on carefully choosing the initial guess for the subsequent numerical optimization.
 |
Point inversion with OpenCascade. |
References
- Ma, Y. L., & Hewitt, W. T. (2003). Point inversion and projection for NURBS curve and surface: Control polygon approach. Computer-Aided Geometric Design, 20(2), 79–99. https://doi.org/10.1016/S0167-8396(03)00021-9 (full-text link)
So what?
Well, I think that events like GSoC and alike offer everything to stimulate the research and development in our CAD domain. While "big boys" are chasing the File System Monster, let's give that industry a new impulse as one day they'll come for our "creepy" mousepads and keyboards. And will suck out our brains.
Want to discuss this? Jump in to our forum.