Why convex hull attribute?
In the article related to the convex hull AAG attributes, I was not clear enough regarding the purpose of this new thingy. Let's put it clearly now:
One could easily see that the convex-only heuristic proposed by [Joshi, S., & Chang, T. C. (1988). Graph-based heuristics for recognition of machined features from a 3D solid model. Computer-Aided Design, 20(2), 58-66] has some important drawbacks when it comes to interacting features:
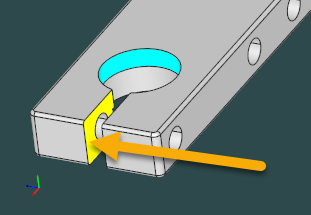 |
A convex-only face is a part of a slot. |
In the image above, the highlighted face has all its neighbors realized through the convex dihedral angles; therefore, it satisfies the convex-only condition. As the classical heuristic says, all such faces should be eliminated from the AAG for the sake of search space reduction. However, this face clearly participates in a slot feature, and its elimination would make slot recognition impossible. In contrast, the convex hull condition does not apply to any but the outer faces of your part. As a trade-off, for some CAD parts, this heuristic might not be as efficient as the convex-only property, but it ensures to never cut off a useful face from the graph.
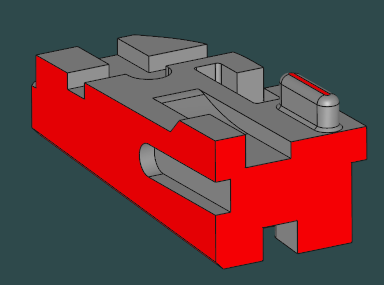 |
A sample part with its convex-hull faces (red color). |
The authors of [Gao, S., & Shah, J. J. (1998). Automatic recognition of interacting machining features based on minimal condition subgraph. Computer-Aided Design, 30(9), 727-739] use the term MFAG (Manufacturing Face Adjacency Graph) for an AAG with all the convex-hull faces eliminated. We read there: "The convex hull (CH) attribute specifies whether the given face coincides with a face of the convex hull of the part or not." So they use this heuristic in the well-known work that claims to deal with feature interactions gracefully (we take their word on that).
To conclude, CH-heuristic is quite computationally expensive compared to the original rule proposed by Joshi and Chang. Also, if your part is tricky enough, the CH rule might not happen to reduce the AAG significantly. However, this new heuristic has one important property: it never cuts off useful faces from the graph, so there is no trade-off for the recognition completeness. If implemented properly, this heuristic is practical enough.
Want to discuss this? Jump in to our forum.