Поиск подграфа AAG
"Discovering that a problem is NP-complete is usually just the beginning of work on that problem." (M. R. Garey and D. S. Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness.)
Преамбула
Распознавание конструктивных элементов средствами библиотеки OpenCascade можно производить различными способами. Наивный метод состоит в написании кода на C++ для итерации граничного представления модели с проверками геометрических типов. Скажем, для распознавания цилиндрических отверстий следует искать тип Geom_CylindricalSurface, а также проверять смежные грани, двугранные углы, типы опорных поверхностей и проч. Такой метод имеет право на жизнь, особенно, если речь идет о решении некоторой специфической задачи распознавания, без претензии на создание механизма (фреймворка) распознавания общего вида. Наивному подходу, однако, присущ целый ряд недостатков:
- Он завязан на конкретное ядро геометрического моделирования.
- Возможности расширения такого подхода крайне сомнительны (приходится писать еще один кусок кода на C++, чтобы добавить новый тип конструктивного элемента в библиотеку распознаваемых типов).
- Расширения недоступны пользователю. Для добавления нового типа надо быть программистом на C++, знать геометрическое ядро и уметь решать подобного рода задачи. Все это в комплексе делает порог вхождения довольно крутым, чему мы неоднократно были свидетелями.
- Программирование новых правил распознавания (на любом языке и с любым ядром моделирования) исключает саму возможность «защиты от дурака». Программист может наделать огромное количество ошибок, начиная от злоупотреблений пакетом TopExp (если говорить о ядре OpenCascade) и заканчивая банальными ошибками кодирования, которые не всегда легко обнаружить. Отсутствие же внятной парадигмы кодирования правил распознавания не позволяет рассчитывать на какие-либо оценки сложности алгоритма, не говоря о масштабируемости или, еще веселее, параллельных вычислениях. Итоговый код будет похож на перепутанный логический клубок, на поверку, однако, лишенный всякой логики. Программирование правил распознавания непосредственно в теле фреймворка — катализатор для архитектуры типа Big Ball of Mud [Foote, B. and Yoder, J. 1997. Big Ball of Mud].
Шагом в светлую сторону является использование формализма теории графов. Апологии AAG мы уделили достаточно места на страницах МГ, поэтому не станем повторять основы. Введение AAG позволяет переформулировать задачу распознавания в терминах поиска некоторого подграфа (шаблона) в исходном графе смежности [Malyshev, A., Slyadnev, S., and Turlapov, V. 2017. Graph-based feature recognition and suppression on the solid models. GraphiCon 2017, 319-322]. Этот подход, хотя и ограничен (он хорошо работает лишь для изолированных конструктивных элементов), дает общий метод решения целого класса задач. Остается чисто технический вопрос: как искать подграф в графе?
Тестовые данные
В качестве тестовой модели построим кубик с глухим цилиндрическим отверстием.
> make-box b; fit > make-cylinder c 0.5 0.5 0.25 0.25 0.75 > bop-cut res b c > set-as-part res; donly > show-aag
 |
Создаем тестовую модель в Analysis Situs. |
Искомое отверстие нетрудно обаружить в графе смежности модели.
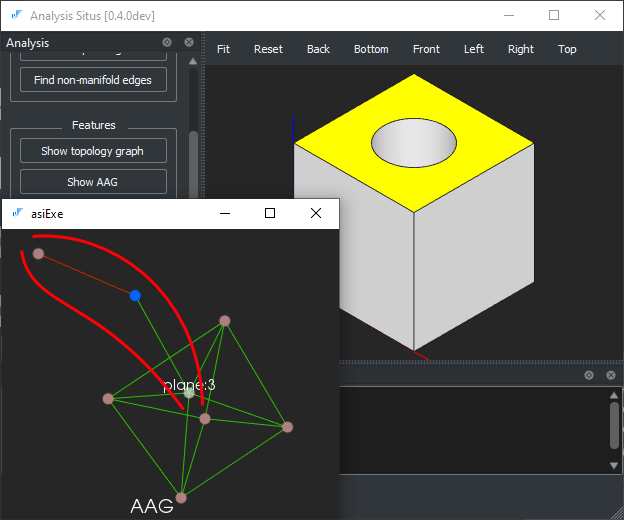 |
AAG и подграф, соответствующий глухому цилиндрическому отверстию (обведен). |
Принцип поиска изоморфизма
Изоморфизм подграфа (subgraph isomorphism) — NP-полная задача (стр. 202, [GT48], [Michael R. Garey and David S. Johnson. Computers and intractability. A guide to the theory of NP-completeness. W. H. Freeman and Company, 1979]).
На web-странице Адриана Ньюмана приведен алгоритм Дж. Ульмана поиска изоморфных подграфов [Ullmann, J.R. 1976. An Algorithm for Subgraph Isomorphism. Journal of the ACM (JACM) 23, 1, 31–42].
Пусть G — матрица смежности полного графа модели (problem graph), P — матрица смежности искомого шаблона (pattern graph). Матрица G для кубика с глухим отверстием имеет следующий вид:
1 2 3 4 5 6 7 8 ----------------+ 0 1 1 1 1 0 0 0 | 1 1 0 1 0 1 1 0 0 | 2 1 1 0 1 0 1 1 0 | 3 1 0 1 0 1 1 0 0 | 4 1 1 0 1 0 1 0 0 | 5 0 1 1 1 1 0 0 0 | 6 0 0 1 0 0 0 0 1 | 7 0 0 0 0 0 0 1 0 | 8
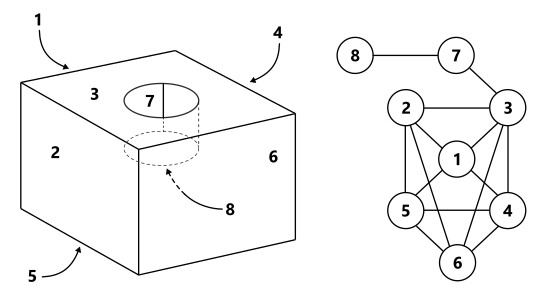 |
Индексация граней и граф смежности. |
Матрица P графа-шаблона имеет вид:
1 2 3 ------+ 0 1 0 | 1 1 0 1 | 2 0 1 0 | 3
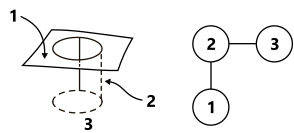 |
Индексация граней конструктивного элемента и его граф смежности. |
Искомую биекцию задает следующая матрица M:
1 2 3 4 5 6 7 8 ----------------+ 0 0 1 0 0 0 0 0 | 1 0 0 0 0 0 0 1 0 | 2 0 0 0 0 0 0 0 1 | 3
В том, что матрица M — это искомая биекция, можно убедиться непосредственной подстановкой M(MG)T = P. Строки матрицы M отвечают вершинам графа-шаблона P, cтолбцы — вершинам графа G. Равенство элемента единице означает, что между двумя данными вершинами установлено соответствие. Таким образом, задача распознавания конструктивных элементов сводится к поиску всех допустимых биекций M.
 |
Проверка выбранного изоморфизма M непосредственной подстановкой в M(MG)T = P. |
Отметим здесь, что матричная проверка M(MG)T = P состоит в последовательном выборе сначала строк матрицы G, а затем столбцов получившейся матрицы. Таким образом, матрица M выступает в качестве фильтра (или маски) биективных отображений P на G.
Алгоритм Ульмана
Алгоритм инициализирует матрицу M всевозможными соответствиями вершин двух графов. Чем больше единиц удается исключить на данном этапе, тем меньше итераций потребуется осуществить. Простейшее правило инициализации состоит в сравнении степеней соответствующих вершин: степень вершины vP графа P не должна превышать степень вершины vG графа G. Руководствуясь этим правилом, нетрудно составить следующее начальное приближение матрицы M:
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1
Мы видим здесь, что единственно невозможным соответствием является биекция 2-8, поскольку вершина 2 графа P имеет степень равную двум, тогда как вершина 8 графа G имеет степень равную единице. Дополнительная эвристика, требующая совпадения типов параметрических поверхностей соответствующих граней, позволяет существенно проредить начальную матрицу M:
1 1 1 1 1 1 0 1 0 0 0 0 0 0 1 0 1 1 1 1 1 1 0 1
Так, мы видим, что вершина 2 графа P может соответствовать только вершине 7 графа G, поскольку это единственно возможное отображение цилиндрических граней. Уже на этапе инициализации можно поставить вопрос о самом существовании изоморфизма. Очевидно, каждая строка матрицы M должна содержать хотя бы одну единицу, т.к. противное означало бы невозможность найти отображение некоторой вершины графа-шаблона на граф G.
Алгоритм поиска изоморфного подграфа концептуально прост. Начиная с зафиксированного состояния матрицы M, следует осуществить перебор всех производных матриц-кандидатов, содержащих в каждой строке ровно одну единицу и в каждом столбце не более одной единицы (иначе отображение не есть биекция). Рекурсивная процедура, осуществляющая такой перебор, проверит изоморфизм на следующем наборе производных матриц:
1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 +-----------------+ | 0 0 1 0 0 0 0 0 | | 0 0 0 0 0 0 1 0 | | 0 0 0 0 0 0 0 1 | +-----------------+ 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 +-----------------+ | 0 0 0 0 0 0 0 1 | | 0 0 0 0 0 0 1 0 | | 0 0 1 0 0 0 0 0 | +-----------------+ 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0
Всего вариантов 42: 7 вариантов выбора первой строки и 6 вариантов выбора третьей для каждого выбора первой. Для N узлов в графе G это правило дает N*(N-1)*(N-2) вариантов при условии, что исходная матрица M не была должным образом разрежена. Если количество вершин в графе P равно K, то итоговая временная сложность алгоритма есть O(N^K), то есть для фиксированных значений K алгоритм имеет полиномиальную (хотя и высокую) сложность.
Листинг с результатами, предъявленный выше, наглядно показывает, что предложенный алгоритм недостаточен для поиска конструктивных элементов. Было найдено два изоморфизма (обведены рамкой), в то время как конструктивный элемент в модели, очевидно, только один. Простейший способ выбрать нужные изоморфизмы — пройтись по дугам графа-шаблона P и сопоставить атрибуты дуг (convex/concave) с соответствующими атрибутами на дугах графа G. Поскольку изоморфизм есть биекция, то на данном этапе для каждой вершины графа P мы имеем однозначный образ в G, и проверка атрибутов не составляет труда.
Возьмем в качестве тестовой биекции матрицу M, имеющую следующий вид:
0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0
Данная матрица предписывает, в частности, что вершина P_1 шаблона P соответствует вершине G_2 графа G (строка 1). Если вершина P_1 отвечает вершине G_2, то соседи вершины P_1 также должны отвечать соседям вершины G_2. То есть, вершина P_2 должна соответствовать одной из вершин G_1, G_3, G_5 или G_6. Если для данной матрицы M это условие не соблюдается, то предполагаемое соответствие (P_1, G_2) можно обнулить. Кроме того, такое обнуление может привести к тому, что в строках матрицы M не окажется единиц, и тогда нет смысла разворачивать рекурсивный поиск дальше. Эти рассуждения соответствуют процедуре Pruning в заметке Адриана Ньюмана, помянутой выше.
Критика
С практической точки зрения, поиск изоморфизмов не дает золотого ключика к решению задачи распознавания. Остаются две существенные проблемы:
- Низкая производительность.
- Отсутствие вариативности по шаблону подграфа.
Низкая производительность алгоритма связана с тем, что он выполняет глобальный перебор всевозможных биекций (напомним, что задача поиска изоморфизмов подграфа NP-полна). Добавление новых эвристик, снижение размерности задачи и другие ухищрения не избавляют от сложности перебора, то есть от оценки O(N^K), хотя и позволяют домножить эту оценку на «хорошую константу».
Кроме того, в приложениях геометрического моделирования шаблоны, как правило, не являются строго фиксированными. Цилиндрическое отверстие может содержать одну или несколько граней-цилиндров, вложенных в одну или несколько опорных поверхностей. Последовательное (да хотя бы и параллельное) нахождение серии изоморфизмов делает задачу распознавания еще более трудоемкой.
"Subgraph isomorphism is NP-complete, and various heuristics suggested in the literature do not break such a complexity barrier. Secondly, and perhaps more importantly, general interactions between features are very difficult to accommodate. The difficulties seem to be inherently associated with approaches based primarily on "topological" information. Face and edge relationships are altered by feature interactions, and it seems impractical to define all the resulting patterns." [Vandenbrande, J.H. and Requicha, A.A.G. 1993. Spatial Reasoning for the Automatic Recognition of Machinable Features in Solid Models. IEEE Transactions on Pattern Analysis and Machine Intelligence 15, 12, 1269-1285]
Замечания по реализации
Даже на CAD-моделях небольшого размера (сотни граней), задача поиска изоморфизмов требует значительных вычислительных ресурсов. Самые изобретательные эвристики не отменяют того факта, что алгоритм Ульмана — это перебор большого числа возможных биекций. Успешная реализация алгоритма, поэтому, требует тщательной проработки по следующим направлениям:
- Выбор максимально производительных структур данных. Траты времени на перепаковку, итерирование и доступ к элементам должны быть минимальны.
- Привлечение «умных» эвристик, позволяющих обнулить как можно больше элементов матрицы M.
- Снижение размерности задачи путем изъятия граней, заведомо не являющихся фичерами. Отметим здесь, что снижение размерности требует сохранения соответствий между индексами матриц G, P, M, используемых в вычислениях, и индексами граней AAG.
- Бок о бок со снижением размерности идет проблема параллельных вычислений. Дело в том, что изъятие граней из AAG нередко приводит к подразбиению последнего на множество компонент связности. Очевидно, поиск изоморфизмов можно осуществлять на каждой компоненте независимо. Есть даже «голоштанная идея» запускать ядро алгоритма на GPU.
Выводы
Поиск изоморфных подграфов — вычислительно интенсивная процедура, не прощающая безолаберного кодирования. В то время как наивный поиск граней в CAD-модели можно написать, не особо заботясь об алгоритмической чистоте и вычислительной сложности, с изоморфизмом этот фокус не пройдет. В то же время, при грамотном программировании с привлечением профилировщика реализовать дееспособный алгоритм, скажем прямо, не великая проблема. О некоторых нюансах, связанных с реализацией и использованием изоморфизмов, мы поговорим в будущем.