Yet another format for exchanging curves and surfaces

Preamble

ASTRA CAD/CAE (Russian «АСТРА» = «Автоматизированная Система Технологических РAсчетов») is a pretty unknown software package being developed in Sobolev Institute of Mathematics (Novosibirsk). The system is closed and there is very little knowledge about it on the Internet.

ASTRA in action.

What one can understand reading the publicly available information is that ASTRA is being used for numerical simulation (including geometric design) of turbomachinery components, while its scope is definitely broader. The system can be traced back to Yu. S. Zaviyalov (Юрий Семенович Завьялов) who was the Soviet/Russian guru of spline functions and their applications.

Yu. S. Zaviyalov (1931-1998).

Our team has got a chance to add interoperability functions for connecting ASTRA and Analysis Situs (feature request #220). The new import/export routines should help CAE engineers in bridging together open source software solutions, such as Salome and Analysis Situs. There are not so many standards for exchanging curves and surfaces in CAGD. And ASTRA provides yet another format for exchanging geometries.

Specific data exchange procedures are often added as plugins, and this was one of the options we considered for implementing in Analysis Situs. However, as of now, Analysis Situs does not provide any "marketplace" for plugins, and this simple fact would make the entire distribution process quite unmaintainable. That is why we decided to keep our software as integral as possible by providing all freely available plugins out of the box. Moreover, since ASTRA mostly supports splines and does not expose any other curve and surface types (except for the surfaces of revolution), we decided to decouple the new data exchange interfaces from OpenCascade and provide them within our simplistic in-house spline kernel named Mobius.

Curves

ASTRA employs a simplistic layout for the definition of curves and surfaces. Each primitive has a name composed of 8 characters, e.g. "40РОПВЛ1" where 40 is the database prefix, "РО" is a volume prefix, and "ПВЛ1" is the name of array. From this data, only array names are exported to the ASTRA files, and we only have to make sure that Unicode characters are processed smoothly.

It is not unusual for anyone who has ever worked in CAE domain to see multidimensional arrays dumped into text files. As long as the indexation is defined, you can serialize and scan a multidimensional block of data as a plain array. E.g., in ASTRA, the curve data can appear packed in the following way:

P_x P_y P_z T_x T_y T_z u
...

Here, the first three coordinates define the curve point (P_x, P_y, P_z). Then, the tangent vector at a point is defined by the corresponding (T_x, T_y, T_z) triplet. The last value in a row is the curve parameter u corresponding to the previously defined point and tangent vector. All curves are specified in the Hermite form, i.e., points are followed by the tangent vectors, and there is no other information about the curve (e.g., its degree).

Hermite to Bezier/B-spline conversion formulae. This document is pretty rare and you wouldn't find it on the Internet (it was prepared specially for ASTRA import/export by Zolotarevich from St. Petersburg). Click on the image to access the PDF file.

To switch from this data to splines, each pair of points (a segment) is interpolated with a Bezier curve of degree 3. Once done, such curves can be concatenated directly to B-spline curves by merging their poles together and repeating knots at the breakpoints 3 times (degree minus one). It's not surprising then that such increased multiplicities at knots yield continuity defects. The good news is that by knot removal (and subsequent adjustment of control points), the continuity defect can be improved up to C1 (instead of C0). The following function working on OpenCascade splines will clean up your curve by removing redundant knots and improving the order of continuity (if possible):

static void SimplifyCurve(Handle(Geom_BSplineCurve)& BS,
                          const double               Tol,
                          const int                  MultMin)
{
  double    tol = Tol;
  int       Mult, ii;
  const int NbK = BS->NbKnots();
  
  for ( Mult = BS->Degree(); Mult > MultMin; Mult-- )
  {
    for ( ii = NbK; ii > 1; ii-- )
    {
      if ( BS->Multiplicity(ii) == Mult )
        BS->RemoveKnot(ii, Mult - 1, tol);
    }
  }
}

Because knot removal, unlike knot insertion, does not preserve shape, we must provide a tolerance to control shape distortion near the removed knots. Since we do not want to distort the original data, the default Precision::Confusion() = 1.e-7 spatial tolerance is used.

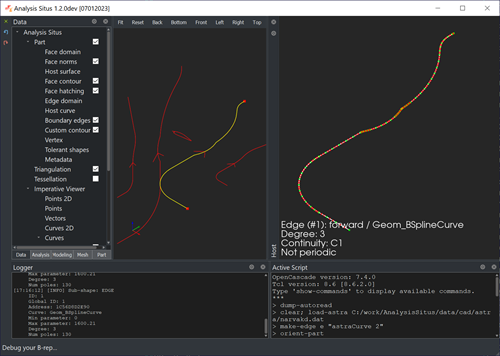B-spline curves imported from ASTRA to Analysis Situs.

Surfaces

We will be talking about two surface types that are supported by ASTRA: spline surfaces and surfaces of revolution.

Splines

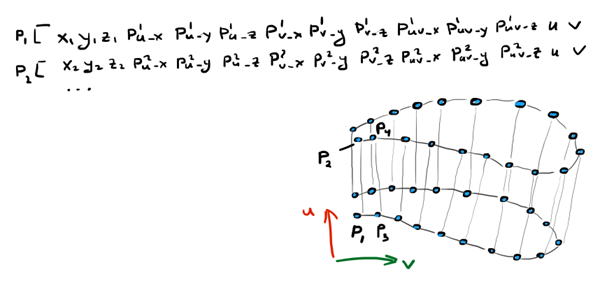
The freeform surface definition is similar to the freeform curve definition in the ASTRA format. Because a parametric surface is a two-variate function s(u,v), we need more data for the Hermite definition of a surface compared to what we need for curves. Each row specifies the 1-st order partials together with the 2-nd order mixed partial derivative at a point. This information is enough to compose a network of Bezier patches that can be later on converted into a single B-spline surface.

P_x P_y P_z Pu_x Pu_y Pu_z Pv_x Pv_y Pv_z Puv_x Puv_y Puv_z u v
...

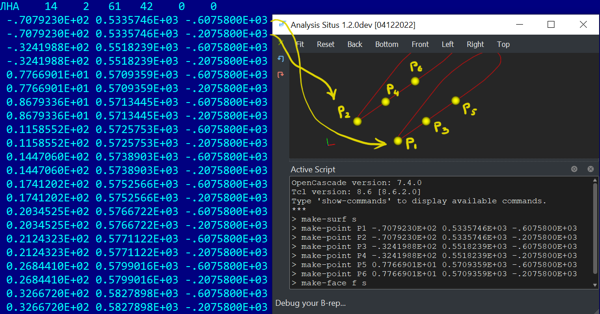
The number of points is defined as nbU * nbV, where nbU is the number of points in the U curvilinear direction, and nbV is the number of points in the V curvilinear direction. These two numbers are specified in the header block of the corresponding array, e.g.:

ЛНА    14    2   61   42    0    0

The values 2 and 61 here define the number of U and V isoparametric lines respectively. The points are arranged in a way to define the isoparametric lines of V continuously (V = const), so that each next point jumps to the next U-isoline as illustrated by the following image:

Order of points in the ASTRA format.

Point-by-point translation from ASTRA curve definition to Analysis Situs.

In Mobius, the control points of spline surfaces are stored in two-dimensional arrays. To switch from a plain array of control points to a two-dimensional array according to the Mobius' conventions, the following mapping is necessary:

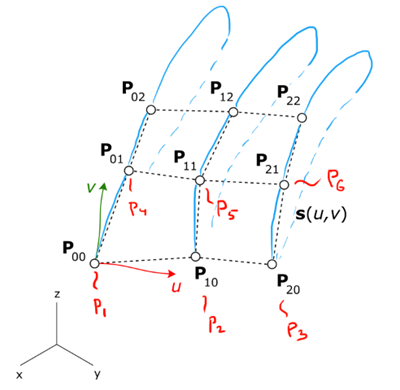Plain array to a network of control points. Blade sections are rendered in blue to aid comprehension, though this entire story is not necessarily related to blades.

The conversion formulae for indices is then as follows:

const int j = (serialIdx - 1) / nbU;
const int i = (serialIdx - 1) % nbU;

Here serialIdx is the plain-array index coming from ASTRA.

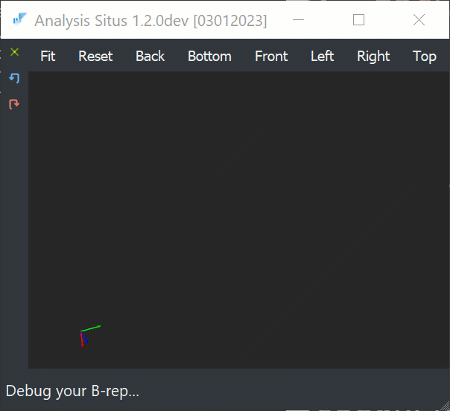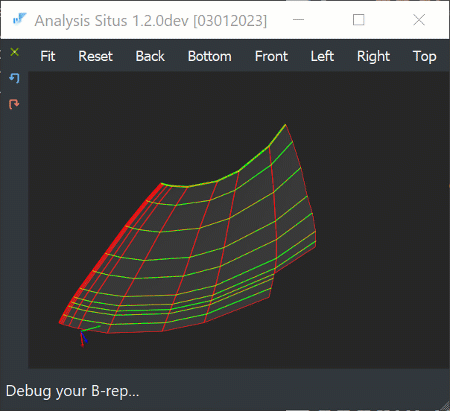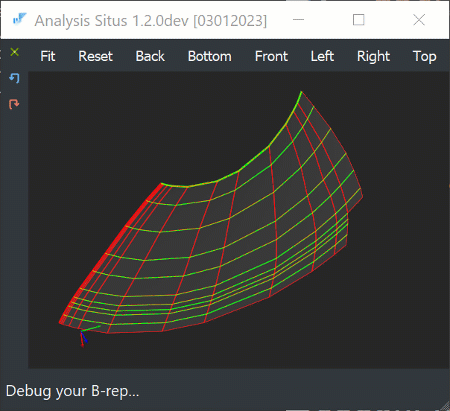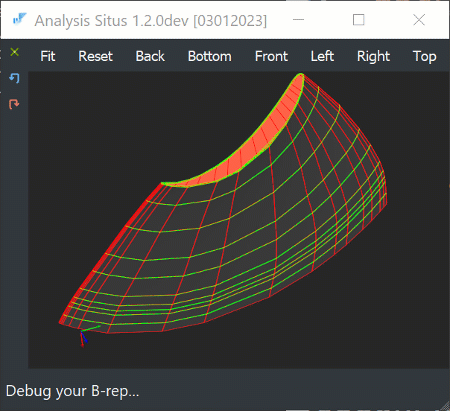Bezier patches as defined by points and derivatives from ASTRA.

Once all third-degree Bezier patches have been added, they must be concatenated into a single surface as defined in the ASTRA format. Because ASTRA cannot express any trimmed surfaces, we assume that the patchwork generated up to this point is inherently rectangular (we will discuss surface untrimming separately in the nearest future). Therefore, concatenation process can be accomplished band-by-band, first joining all patches in the U direction, and then concatenating the obtained bands in the V direction.

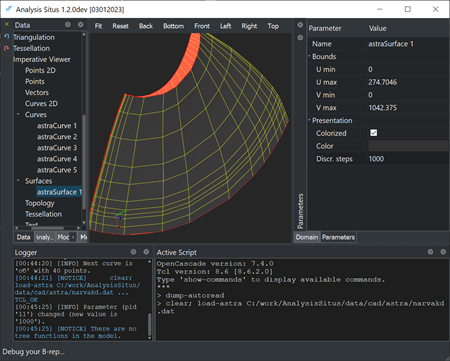Blade surface imported from ASTRA.

Improving of C0 continuity order up to C1 can be done for B-spline surfaces similarly to what we did for curves:

static void SimplifySurface(Handle(Geom_BSplineSurface)& BS,
                            const double                 Tol,
                            const int                    MultMin)
{
  int  multU, multV, ii;
  bool Ok;
  
  const TColStd_Array1OfReal&    U  = BS->UKnots();
  const TColStd_Array1OfReal&    V  = BS->VKnots();
  const TColStd_Array1OfInteger& UM = BS->UMultiplicities();
  const TColStd_Array1OfInteger& VM = BS->VMultiplicities();
  
  for ( ii = U.Length() - 1; ii > 1; ii-- )
  {
    Ok    = true;
    multU = UM.Value(ii) - 1;
    for  ( ; Ok && multU > MultMin; multU-- )
    {
      Ok = BS->RemoveUKnot(ii, multU, Tol);
    }
  }
  
  for ( ii = V.Length() - 1; ii > 1; ii-- )
  {
    Ok    = true;
    multV = VM.Value(ii) - 1;
    for  ( ; Ok && multV > MultMin; multV-- )
    {
      Ok = BS->RemoveVKnot(ii, multV, Tol);
    }
  }
}

Surfaces of revolution

A surface of revolution is defined by its meridian curve (spline) and the axis. Such definition is sort of procedural and matches the definition of the same surface type in OpenCascade.

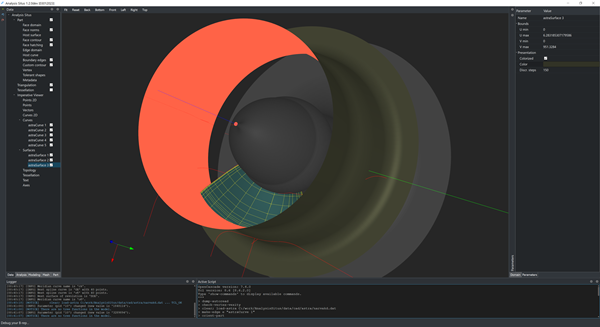Surfaces of revolution corresponding to a hub and a shroud of a turbine.

Here is the small excerpt corresponding to the definition of a surface of revolution in ASTRA:

ПСТ     8    1    1   41    0    0
99**ст     0.0000000E+00 0.0000000E+00 0.0000000E+00
           0.0000000E+00 0.0000000E+00 0.1000000E+01

It's actually nothing but a reference to the meridian curve (spline) and the corresponding axis of revolution.

Surface of revolution rendered by points in the Mobius' native 3D viewer.

Implementation and stuff

ASTRA import procedure is implemented in our open-sourced Mobius spline kernel library. Check it out in the corresponding geom_ReadAstra utility class.

One interesting bug we got in the implementation was related to how control points of Bezier patches are computed. The formulae by Zolotarevich were initially ported from a Python script where expressions like 1/3 are totally fine. In C++, however, you should be careful to write the same thing as 1./3. as otherwise you'll end up with numerical zero (integer division). Funny enough, this typical code mistake leads to quite interesting surface shape which is formally C1 but has visible continuity defects.

Not all equal surfaces are equal.

In this specific case, each Bezier patch has got 16 control points (4x4 control network for the 3-degree patch) but only 4 of them are distinct.

Bad and the corrected surface in Fusion360.

To load an ASTRA file in Analysis Situs, use the following command:

> load-astra <filename>

Bonus

In continuation of this.

The journey to the location was quite memorable. The road direction is a cutting corner along Volga: the goal is to reach another city on the same river. Down the road, you pass through the territories with a pretty obscure history. These are not originally Moscowian and were initially settled by Mordvins, Mari people and potentially even Meryans in the legendary past. You cross the Sura river, where Ivan the Forth made a forepost on his way to take Kazan. You go around Alatyr city, whose name means "heart stone," and it's strange to see a city with such a fabulous name in modern times and so close to our location.

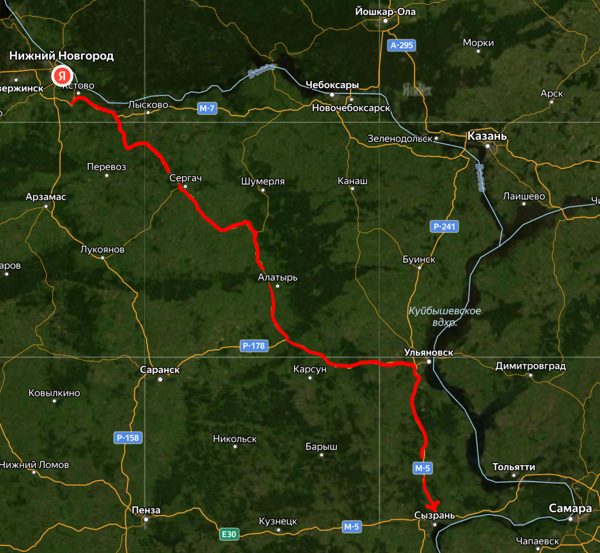Road for corner cutting Volga.

This time, I was probably too eager to make these 600 km as quickly as possible and did not took time to make any good photos. The entire journey was in the dark, and all of these historical sites appeared as ghosts along the mostly empty winter road, which was another challenge. Yes, I would love to take this short trip again (600 km is nothing in Russia) with more time to look around.

Want to discuss this? Jump in to our forum.