Проверка контура грани на замкнутость
Визуализация в программе Analysis Situs, по замыслу, должна быть устойчива к аномалиям в геометрии CAD-модели. Более того, в силу своей специфики («дебаг B-Rep'а»), приложение должно указывать аномальные зоны, облегчать их поиск. Говорить об устойчивой визуализации граничных моделей мы сегодня не будем, но рассмотрим один частный ингридиент этой проблемы.
Известно, что визуализация CAD-модели начинается с подготовки фасетов, то есть триангуляции. Подпрограмма триангуляции (фасетер) производит полигональные подложки для каждой грани, разбивая непрерывные поверхности граничного представления, скажем, по критерию Делоне. Для успешной триангуляции требуется, чтобы лоскут поверхности был ограничен, то есть в параметрическом пространстве грани существовал замкнутый контур (корректно, притом, ориентированный). Например, такой (цветом показана топологическая ориентация, стрелками — геометрическая):
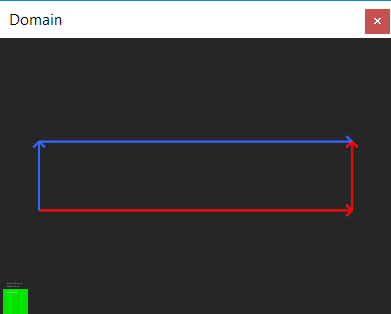
А вот пример «плохого» контура:
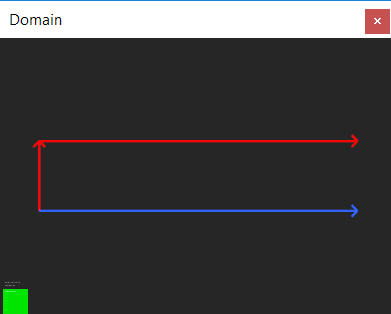
На практике встречаются и совсем убитые контуры, по которым непонятно даже, какой части не хватает:

Чаще всего такие проблемы возникают в результате обмена данными между разнородными геометрическими системами. Например, чтобы загрузить деталь из, скажем, SolidWorks в экосистему OpenCascade, потребуется сначала сохранить модель в нейтральный формат (почти всегда это будет STEP) одним транслятором (неидеальным!), а потом загрузить другим (тоже неидеальным). То есть получается типичный пример перемножения надежности. Для простых моделей проблем, скорее всего, не будет. А вот более сложные могут содержать сюрпризы. Вот пример акулы, которая болеет незамкнутыми контурами («больная» геометрия отрисована красным):

А вот деталь, где границы пары граней почти полностью потерялись:
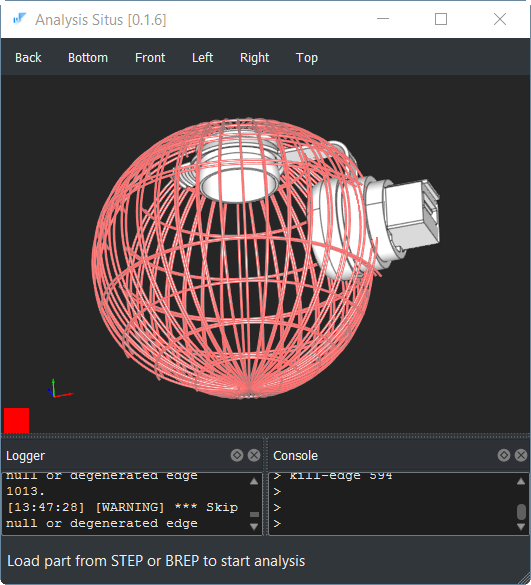
В обоих случаях мы информируем пользователя о проблеме путем отрисовки кроваво-красных изолиний вместо фасетов. Бывает, правда, и так, что фасетер настолько продвинут, что выпадение границ из контура может быть им успешно обработано. Мы этого не допускаем, так как для надежного анализа моделей (а это цель проекта) все проблемы должны быть на виду. Точнее, в нашем случае, фасетер работает всегда, а вот доверять его результатам или нет — зависит от анализа каждой грани на корректность.
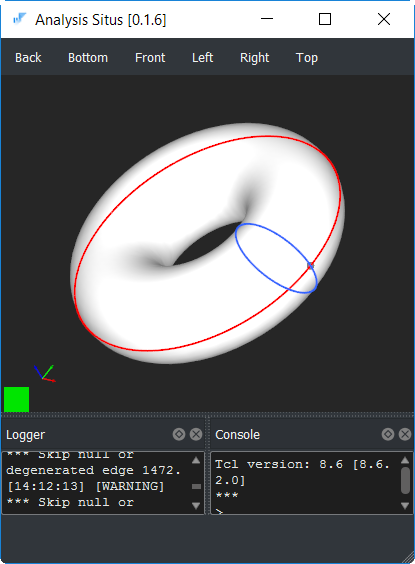
Метод проверки контура на замкнутость концептуально прост. Ключевой момент состоит в том, что проверка реализуется в параметрическом пространстве грани, то есть в 2D, а не в 3D. Мы начали с того, что корректная грань всегда определяется некоторой замкнутой областью в параметрическом пространстве. Эту область легко обнаружить в 2D, тогда как в пространстве моделирования (3D) возможны трудно интерпретируемые конфигурации. Взять, например, тор:
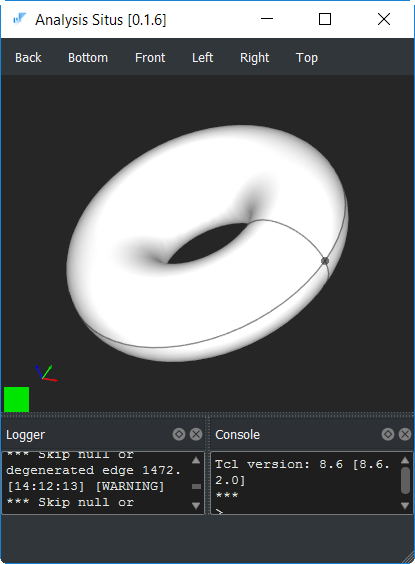
Конфигурация его ребер в 3D не очерчивает замкнутого контура. Это две соприкасающиеся окружности.
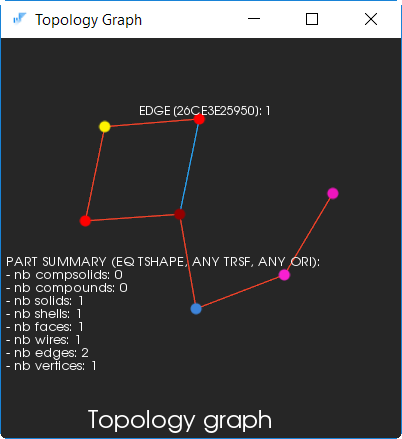
Тор — это вообще интересный объект с точки зрения топологии. Действительно, из топологического графа (рисунок ниже) видно, что тор содержит всего два ребра и одну вершину. На основании этой информации невозможно сделать никаких выводов о замкнутости контура и «самочувствии» единственной (в этом случае) грани.
Однако с параметрическим пространством тора все куда проще. Оба его ребра являются «шовными» (то есть идущими по периоду поверхности), отчего мы имеем не две, а 4 параметрические кривые, которые и складываются в искомый замкнутый контур.
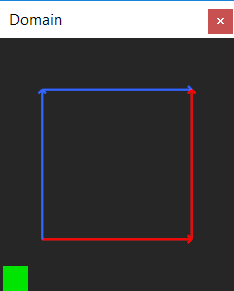
Это нетрудно понять. Тор — параметрическая поверхность, в которой параметры u и v — это два угла, изменяющиеся от нуля до 360-ти градусов. Таким образом, в параметрическом пространстве областью определения тора является квадрат со стороной два пи.
Идея проверки на замкнутость состоит в том, чтобы проанализировать многообразность стыков между параметрическими кривыми в 2D. Почему в 2D — уже понятно, а что там с многообразиями? Тут все просто. Мы утверждаем, что каждый контур корректной грани (а их может быть несколько) топологически эквивалентен окружности. Для любой внутренней точки кривой это очевидно: ее окрестность локально гомеоморфна окружности. Проблемы могут возникнуть только на стыках — их и надо исследовать.
Для проверки многообразности контура каждый стык между параметрическими кривыми ребер анализируется на валентность — количество уникальных кривых, геометрически соседствующих а данной вершине. Вот пример «хорошего», многообразного стыка с валентностью точки стыка равной двум:
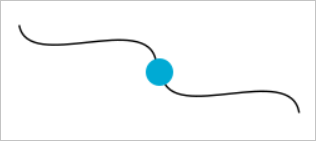
Немногообразный стык валентности 1 выглядит так:
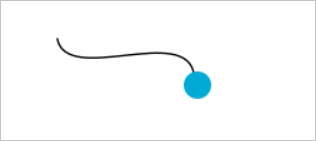
А вот валентность 3:
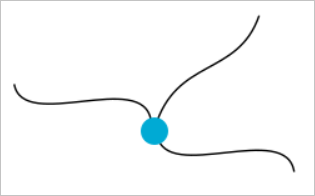
Контур грани объявляется корректным, если все стыки многообразны, то есть имеют валентность 2. При этом под «стыком» понимается не топологическая вершина, а просто концевая точка, снятая с ребра в силу его параметрической кривой.