Простейшая интерполяция кривой без ограничений
Постановка задачи
Пусть имеется набор неповторяющихся точек ${Q_k}$, где $k \in {0, 1, ..., n}$. Требуется построить кривую, точно проходящую через данные точки. Как эластичную нить можно протянуть через неподвижные бусины несчетным числом способов, так и задача интерполяции имеет бесконечное множество решений.
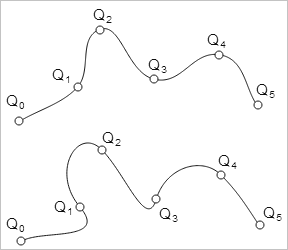
Рис. 1: задача интерполяции имеет бесконечное множество решений.
Воспользуемся уравнением B-кривой степени $p$ для ее решения:
$C(u) = \sum_{i=0}^n N_{i,p}(u) P_i$
Здесь:
- $C(u)$ — результирующая кривая (интерполянт);
- $N_{i,p}(u)$ — базисная B-сплайн функция степени $p$;
- $P_i$ — контрольная точка кривой (не точка для интерполирования!).
Кривая $C(u)$ является интерполянтом, если существует набор параметров ${\bar{u}_k}$ таких, что значение кривой для этих параметров совпадает с целевыми точками ${Q_k}$, где $k \in {0, 1, ..., n}$:
$C(\bar{u}_k) = \sum_{i=0}^n N_{i,p}(\bar{u}_k) P_i = Q_k$ : (1)
Выражение (1) определяет систему линейных алгебраических уравнений (СЛАУ) относительно координат точек контрольного полигона ${P_k}$ в случае, если набор параметров ${\bar{u}_k}$ и базис ${N_{i,p}}$ заранее выбраны. Напомним, что базисная B-сплайн функция определяется через реккурентные соотношения Кокса де Бора:
$N_{i,0}(u) = 0, u \notin [u_i, u_{i+1})$
$N_{i,0}(u) = 1, u \in [u_i, u_{i+1})$
$N_{i,p} = \frac{u-u_i}{u_{i+p}-u_i}N_{i,p-1}(u) + \frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}N_{i+1,p-1}(u)$
Таким образом, для решения задачи интерполяции достаточно применить следующую процедуру:
- Выбрать значения параметров ${\bar{u}_k}$;
- Выбрать степень базисных B-сплайн фукнций $p$;
- Выбрать узловой вектор $U$;
- Решить СЛАУ (1).
Очевидно, что если пункты 1, 2 и 3 требуют некоторого выбора, то этот выбор может быть осуществлен оптимальным (в некотором смысле) образом. Действительно, разумно поставить задачу оптимизации выбора параметризации кривой и искать необходимые значения в силу некоторого критерия оптимальности. Однако на практике часто бывает достаточно следовать определенной методике, которая хорошо зарекомендовала себя в области CAD-моделирования. Ниже мы опишем эту методику, оговорившись, что единственным критерием оптимальности для нас является субъективно воспринимаемая «оправданность» поведения интерполянта. Этот «критерий» мы оставим без строгого математического выражения и сформулируем его словестно: результирующая кривая не должна иметь «извивов», не обоснованных наличием исходных точек. Такой критерий наиболее близко отражает ожидания пользователя, применяющего алгоритм интерполяции. Степень базисных B-сплайн функций обычно выбирается невысокой (например, 3). Ниже мы проведем несколько экспериментов, чтобы увидеть каково влияние степени на поведение результирующей кривой.
Выбор параметров на кривой
Выше мы проводили аналогию между интеполяцией и пропуском нити через неподвижные бусины. Если допустить, что кривая параметризуется по длине (натуральная параметризация), то выбор параметров ${\bar{u}_k}$ позволяет нам отсечь длины сегментов нити между бусинами.
Мы рассмотрим три широко известных подхода к выбору параметров интерполянта:
- Равномерная параметризация,
- Хордовая параметризация.
- Центростремительная параметризация.
Договоримся также впредь рассматривать только нормированную параметризацию, т.е. значения параметров всегда находятся в отрезке $[0;1]$.
Равномерная параметризация
Простейший способ выбора параметров ${\bar{u}_k}$ — равномерное распределение на числовом отрезке как показано ниже:
$\bar{u}_0 = 0, \bar{u}_1 = \frac{1}{n}, ..., \bar{u}_k = \frac{k}{n}, ..., \bar{u}_n = 1$

Рис. 2: равномерная параметризация.
Забегая немного вперед, приведем типичный результат интерполяции с использованием равномерной сетки параметров:
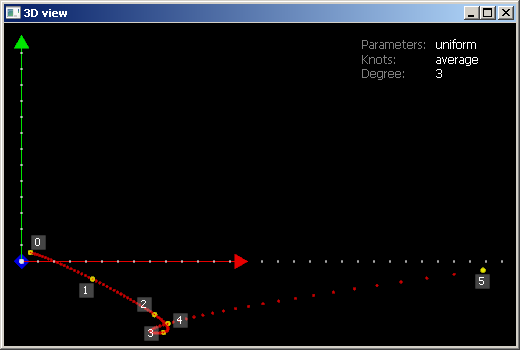
Рис. 3: интерполянт на равномерном разбиении параметрического интервала.
На рис. 3 кривая изображена точками, снятыми с некоторым (достаточно репрезентативным) параметрическим шагом. Таким образом, каждому значению параметра, растущего с фиксированной величиной шага, соответствует точка на кривой. Нетрудно видеть, что на коротких интервалах точки расположены плотно, тогда как на протяженных участках — разреженно. Таким образом, для некоторого параметрического приращения $\Delta{u}$ кривая пробегается материальной точкой быстрее на протяженных участках, так как модуль соответствующего вектора перемещения $|C(u + \Delta{u}) - C(u)|$, очевидно, больше. В рассмотренном примере использовались 6 целевых точек с монотонно возрастающей координатой $x$. Мы видим, что результирующая кривая образует петлю на точках с индексами 2, 3 и 4. Такое поведение интерполянта редко бывает допустимо в геометрическом моделировании, так как кривые с самопересечениями обычно считаются некорректными (например, в случае использования их для построения ребер при B-Rep моделировании).
Хордовая параметризация
Чтобы учесть расстояния между целевыми точками и приблизить параметризацию к натуральной, широко используется выбор параметров по хордовой длине (chord length). Длина $d$ полигона, построенного на точках ${Q_k}$, выражается следующим образом:
$d = \sum_{k=1}^{k=n}{|Q_k - Q_{k-1}|}$
Для каждой точки параметр выбирается по формуле:
$\bar{u}_k = \bar{u}_{k-1} + \frac{|Q_k - Q_{k-1}|}{d}$
Здесь $k \in {1, 2, ..., n-1}$, причем:
$\bar{u}_0 = 0; \bar{u}_n = 1$
Вернемся к примеру рассмотренному выше. Кривая, построенная при помощи хордовой параметризации, принимает вид, показанный на рис. 4.

Рис. 4: интерполянт при хордовой параметризации.
Из рис. 4 видно, что петля исчезла. Однако интерполянт теперь имеет неоправданный «извив» между последней и предпоследней точками. Несмотря на то, что поведение кривой математически корректно (она точно проходит через целевые точки), результат скорее всего окажется неожиданным для пользователя. Так или иначе, на практике метод хорд зарекомендовал себя довольно неплохо. В случае, если расстояние между точками не варьируется сильно, этот подход дает удовлетворительные результаты. Нетрудно также видеть, что в случае равномерного распределения точек этот метод идентичен предыдущему.
Центростремительная параметризация
Выше мы увидели, что хордовый метод помогает отсечь петли результирующего интерполянта за счет более адекватного подбора параметров. В отличие от равномерного распределения, в хордовой шкале учитываются расстояния между точками. Однако даже в этом случае поведение кривой может оказаться неудовлетворительным, прежде всего из-за того, что интерполянт слишком далеко отходит от ломаной, проведенной через целевые точки (рис. 5).
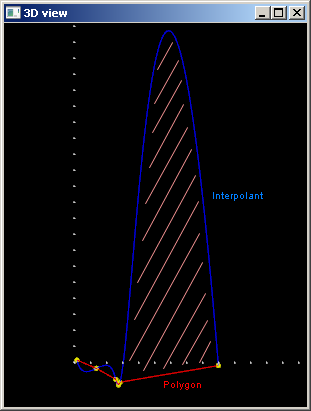
Рис. 5: интерполянт на хордовой сетке и его управляющая ломаная.
В работе [Lee89] предложен способ выбора параметров, исходя из интуитивных кинематических соображений. Автор замечает, что хордовая параметризация является прежде всего грубым приближением натуральной параметризации, целесообразность применения которой в задачах интерполяции никак не обосновывается. Вместо этого можно рассмотреть задачу движения автомобиля через набор контрольных пунктов с наибольшим комфортом для водителя. Интуитивно ясно, что для комфортной езды автомобиль должен сбавлять скорость на поворотах. В случае использования хордовой параметризации мы, напротив, стремимся сохранить примерно одинаковую скорость автомобиля между контрольными пунктами, что выглядит неоправдано.
Предположим, что $C(u)$ — результирующая кривая (траектория движения автомобиля). Имея эту кривую, можно ввести ее натуральную параметризацию $C(s)$, где $s$ — длина дуги. Очевидно, каждому значению параметра построения $u$ соответствует некоторое значение натурального параметра, т.е. $s = s(u)$. Запишем выражение для второй производной интерполянта по исходному параметру:
$\frac{d^2 C}{du^2} = \frac{d}{du} \left ( \frac{dC}{du} \right ) = \frac{d}{du} \left ( \frac{dC}{ds}\frac{ds}{du} \right ) = \frac{d^2 C}{ds^2}{\left(\frac{ds}{du}\right)}^2 + \frac{dC}{ds} \frac{d^2 s}{du^2}$
Мы совершили переход к натуральной параметризации для того, чтобы воспользоваться ее известными дифференциальными характеристиками в канонической форме:
$\frac{dC}{ds} = \overrightarrow{T}$ : (2)
$\frac{d^2 C}{ds^2} = \kappa \overrightarrow{N}$ : (3)
Выражение (2) определяет касательный вектор к кривой, причем $|\overrightarrow{T}| = 1$.
Выражение (3) определяет кривизну $\kappa$ и вектор нормали, причем $|\overrightarrow{N}| = 1$.
Окончательно имеем следующее выражение для второй производной по исходному параметру:
$\frac{d^2 C}{du^2} = \kappa \overrightarrow{N}{\left(\frac{ds}{du}\right)}^2 + \overrightarrow{T} \frac{d^2 s}{du^2}$
Договоримся искать такую параметризацию $s(u)$, чтобы членом ${d^2 s}/{du^2}$ можно было перенебречь. С кинематической точки зрения (принимая $u$ за время) это означает, что касательное ускорение автомобиля равно нулю, т.е. водитель не ускоряется на прямолинейных участках пути (движется равномерно). В результате этого упрощения имеем:
$\frac{d^2 C}{du^2} = \kappa \overrightarrow{N}{\left(\frac{ds}{du}\right)}^2$
Это выражение определяет осестремительное ускорение автомобиля. Теперь задача состоит в том, чтобы оценить время прибытия $u_i$ автомобиля в каждую точку $P_i$. Пренебрежение касательным ускорением здесь играет ключевую роль, так как указанная оценка была бы невозможна в случае, если водитель мог произвольным образом ускорять свое движение.
Следующее упрощение состоит в переходе от производной к конечной разности. Скорость движения автомобиля может быть приблизительно расчитана как отношение пройденного расстояния на время в пути:
$\frac{ds}{du} = \frac{|Q_i - Q_{i-1}|}{u_i - u_{i-1}}$
Запишем теперь выражение для кривизны, которая, как известно, есть модуль второй производной, взятой по натуральному параметру кривой.
$\kappa = \left|\frac{d}{ds}\left(\frac{dC}{ds}\right)\right| = \left|\frac{d\overrightarrow{T}}{ds}\right|$
Последняя формула выражает изменение направления касательной при бесконечно малой вариации длины дуги. Таким образом можно приблизительно записать:
$\kappa = \frac{|\overrightarrow{T_i} - \overrightarrow{T}_{i-1}|}{|Q_i - Q_{i-1}|}$
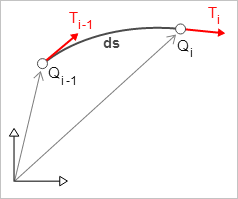
Рис. 6: касательные в точках интерполянта.
Из геометрических соображений нетрудно видеть, что изменение касательной можно представить через угол вращения касательного вектора между двумя точками (рис. 7).
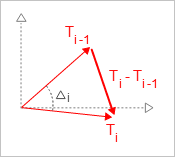
Рис. 7: угол между касательными векторами.
Причем:
$|\overrightarrow{T_i} - \overrightarrow{T}_{i-1}| = |\overrightarrow{T_i}|\sin{\frac{\Delta_i}{2}} + |\overrightarrow{T}_{i-1}|\sin{\frac{\Delta_i}{2}} = 2\sin{\frac{\Delta_i}{2}}$
Допуская, что интерполянт достаточно гладкий (на кривой нет изломов), мы можем предположить, что малому изменению длины дуги $s$ соответствует малое изменение касательной. Это означает, что угол $\Delta_i \ll 1$. Таким образом имеем:
$|\overrightarrow{T_i} - \overrightarrow{T}_{i-1}| = \Delta_i$
Следовательно, выражение для кривизны может быть упрощено:
$\kappa = \frac{\Delta_i}{|Q_i - Q_{i-1}|}$
Наконец, постулируется, что центростремительная сила, действующая на водителя, должна быть пропорциональна углу $\Delta_i$ ([Lee89]). В этом случае можно записать:
$F = m \frac{d^2 C}{du^2} = a \Delta_i$
Здесь $m$ — масса материальной точки, $a$ — некоторый коэффициент в силу нашего постулата о пропорциональности силы углу поворота. Используя выражение для второй производной, имеем:
$\kappa {\left(\frac{ds}{du}\right)}^2 = \tilde{a} \Delta_i$
Здесь $\tilde{a}$ есть некоторый новый коэффициент, значением которого мы можем управлять. Используя этот коэффициент запишем:
$\frac{|Q_i - Q_{i-1}|}{(u_i - u_{i-1})^2} = \tilde{a}$
Наконец, мы получаем выражение для времени, необходимого, чтобы добраться из пункта $Q_{i-1}$ в $Q_i$:
$u_i - u_{i-1} = \hat{a} \sqrt{|Q_i - Q_{i-1}|}$
Здесь $\hat{a}$ — новое обозначение для произвольно выбираемого коэффициента, принятое для упрощения. Нормализуем временные интервалы, полагая $u_0 = 0$ и $u_n = 1$.
$u_0 = 0$
$u_1 = u_0 + \hat{a} \sqrt{|Q_1 - Q_{0}|}$
$u_2 = u_1 + \hat{a} \sqrt{|Q_2 - Q_{1}|}$
$...$
$u_n = u_{n-1} + \hat{a} \sqrt{|Q_n - Q_{n-1}|} = \hat{a} \sum_{j=1}^{n}\sqrt{|Q_j - Q_{j-1}|} = 1$
Таким образом, получаем выражение для $\hat{a}$:
$\hat{a} = \frac{1}{\sum_{j=1}^{n}\sqrt{|Q_j - Q_{j-1}|}}$
Окончательно имеем следующие формулы для параметров ${u_i}$:
$u_0 = 0$
$u_i = u_{i-1} + \frac{\sqrt{Q_i - Q_{i-1}}}{\sum_{j=1}^{n}\sqrt{|Q_j - Q_{j-1}|}}$
$u_n = 1$
Выбор параметров в соответствии с предложенной схемой часто позволяет уменьшить осцилляции интерполянта между целевыми точками (рис. 8).
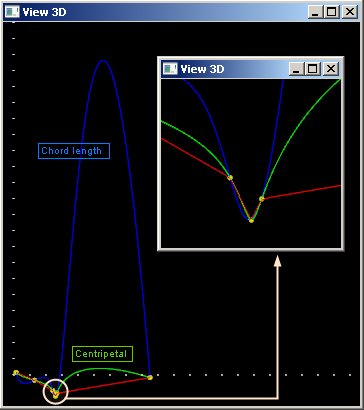
Рис. 8: центростремительная параметризация (зеленая кривая), хордовая параметризация (синяя кривая) и характеристический полигон (красная ломаная).
Нетрудно видеть, что скорость центростремительной параметризации в среднем ниже скорости хордовой параметризации (рис. 9).
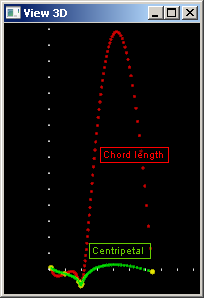
Рис. 9: сравнение скоростей для разных способов выбора параметризации.
Дополнительно о различиях
В работе [Yak05] делается попытка найти «наилучший» способ параметризации в смысле наилучшей обусловленности некоторой системы линейных алгебраических уравнений, из которой находится интерполянт. Обусловленность характеризует, насколько сильно изменится решение при незначительной модификации исходных параметров системы (плохо обусловленные системы ведут себя неустойчиво). Показано, что в смысле введенного критерия обусловленности, натуральная параметризация является наилучшей. Так как хордовая параметризация дает первое приближение натуральной, то именно этот способ рекомендован в [Yak05] как наилучший. Тем не менее, выше мы увидели, что исходя из интуитивных геометрических соображений, результаты хордовой интерполяции могут оказаться не вполне адекватными.
В работе [Yak05] представлен еще один пример (1.9.10), иллюстрирующий различия между хордовой и центростремительной параметризациями. В этом примере по набору из нескольких опорных точек восстанавливается кривая, изображающая скрипичный ключ (рис. 10).
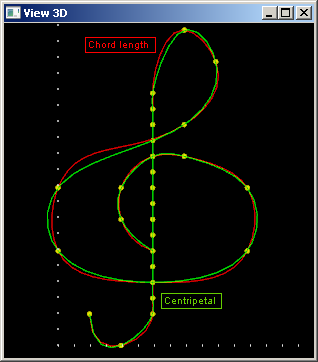
Рис. 10: сравнение разных способов выбора параметризации.
В обоих случаях форма интерполянта в целом оказывается удовлетворительной. Некоторые расхождения хорошо заметны на изгибах кривой, где хордовая параметризация может давать чуть более предпочтительные результаты (рис. 11).
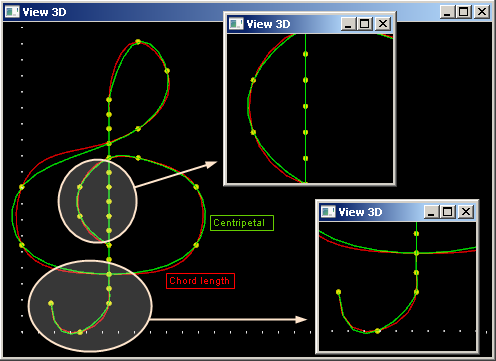
Рис. 11: сравнение разных способов выбора параметризации.
Следует заметить, что в приведенном примере используется большое количество целевых точек, многие из которых выглядят избыточными в смысле определения конечной формы. Рассмотрим случай с пониженным содержанием точек (рис. 12).
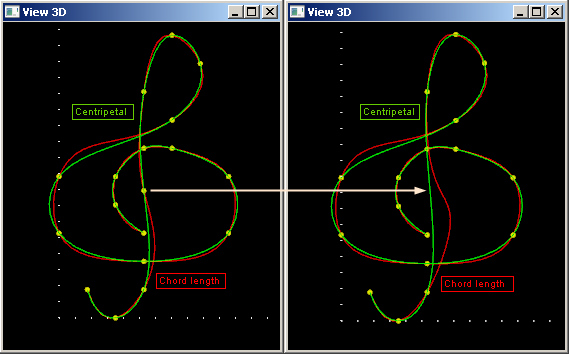
Рис. 12: сравнение разных способов выбора параметризации.
Из рис. 12 легко видеть, что хордовая параметризация дает в целом большую кривизну интерполянта. Поэтому для ее применения на реальных наборах данных желательно, чтобы целевые точки были расположены как можно более плотно.
B диссертации [Yak05] показано, что натурально параметризованный интерполянт наиболее предпочтителен с вычислительной точки зрения. Но что хорошо компьютеру, то не всегда хорошо человеку. Стремление параметризовать интерполянт по длине дуги кривой нередко приводит к неожиданной форме результата, что очень важно в приложении аппарата интерполяции к CAGD.
- [Pieg97] Piegl, L., and Tiller, W., The NURBS Book, 1997.
- [Lee89] Lee, E.T.Y., Choosing nodes in parametric curve interpolation, 1989.
- [Yak05] Якимович, А. Ю., Наилучшая параметризация в задачах приближения кривых и поверхностей, 2005.