Моделирование трубки (pipe) в OpenCascade
Сегодня мы выполним небольшое упражнение на моделирование трубки с использованием каскейда.
Классика жанра
Допустим, что нам нужна модель следующего вида:
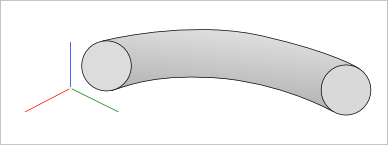
Стандартный способ построения такой геометрии дает класс GeomFill_Pipe. Для его использования нам потребуется задать профиль и траекторию, вдоль которой данный профиль будет протягиваться. Это так называемый кинематический способ построения, широко известный среди проектировщиков. Код простой как лом в разрезе:
// Initialize some path (we use Bezier here for fun) TColgp_Array1OfPnt pathPoles(1, 4); pathPoles(1) = gp_Pnt(0.0, 0.0, 0.0); pathPoles(2) = gp_Pnt(50.0, 10.0, 0.0); pathPoles(3) = gp_Pnt(70.0, 40.0, 0.0); pathPoles(4) = gp_Pnt(150.0, 30.0, 0.0); Handle(Geom_BezierCurve) path = new Geom_BezierCurve(pathPoles); // Radius const double R = 10.0; // Construct pipe GeomFill_Pipe Pipe(path, R); Pipe.Perform(); // Get the result const Handle(Geom_Surface)& S = Pipe.Surface();
В результате мы получаем трубку. Быстро и просто.

Базовой поверхностью трубки оказывается B-поверхность. Все довольно стандартно.

Более подробно говорить об утилите GeomFill_Pipe бессмысленно: исходники открыты, и каждый может почитать вариации API самостоятельно. Отметим только, что мы воспользовались чисто геометрическим API, тогда как есть варианты и для работы с топологией, например, BRepFill_Pipe.
Моделируем переменный радиус
Допустим теперь, что постоянный радиус вдоль траектории нас не устраивает. Т.е. на самом деле мы хотим построить что-то в следующем духе:
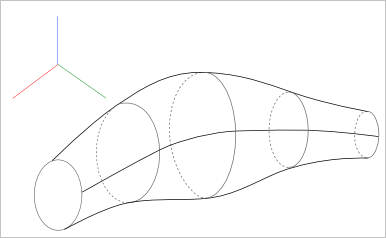
По сравнению с предыдущим случаем здесь налицо переменный радиус сечения вдоль траектории. Само сечение при этом остается круговым, т.е. симметрия трубки не нарушена (иначе это уже не трубка). Проблема перестает быть тривиальной. Утилита GeomFill_Pipe оказывается непригодной, нам нужен другой подход.
Скиннинг
Обратимся сначала к утилите скиннинга (англ. skinning — «натягивание кожи»), а именно к классу BRepOffsetAPI_ThruSections. Скиннинг — это протягивание поверхности через набор сечений. Его классическим приложением является моделирование корабельных корпусов. Да, трубка не похожа на корабль, но ведь и алгоритм не станет разбираться с гидродинамикой профиля. Поперечных сечений для трубки мы можем нарезать сколько угодно, поставив опорные кривые в характерных местах изгиба. Все сечения элементарны, и не должны вызвать затруднений для обобщенного аппарата скиннинга. Что ж, посмотрим, насколько такой вариант перспективен. Ниже мы пытаемся задействовать следующий код:
TopoDS_Shape MakeSkin(const TopTools_SequenceOfShape& wires)
{
// Initialize and build
BRepOffsetAPI_ThruSections ThruSections;
//
for ( int k = 1; k <= wires.Length(); ++k )
{
if ( wires(k).ShapeType() != TopAbs_WIRE )
{
std::cout << "Warning: section " << k << " is not a wire" << std::endl;
continue;
}
//
ThruSections.AddWire( TopoDS::Wire( wires(k) ) );
}
try
{
ThruSections.Build();
}
catch ( ... )
{
std::cout << "Error: crash in BRepOffsetAPI_ThruSections" << std::endl;
return TopoDS_Shape();
}
//
if ( !ThruSections.IsDone() )
{
std::cout << "Error: IsDone() false in BRepOffsetAPI_ThruSections" << std::endl;
return TopoDS_Shape();
}
// Return the result
return ThruSections.Shape();
}
Начинаем с двух сечений:
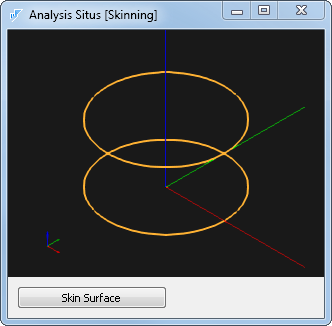
Результат очевиден:
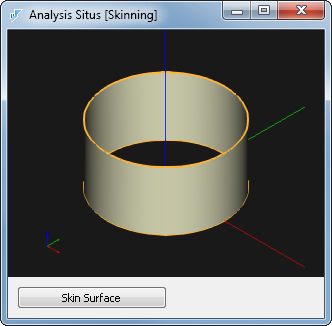
В основании лежит обрезанная цилиндрическая поверхность:
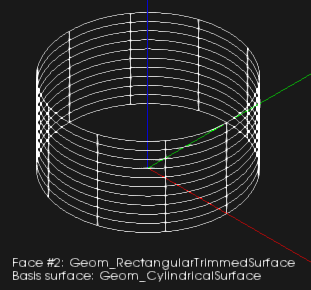
Теперь незначительно отредактируем верхнее сечение. Дадим ему небольшой угол поворота и сместим с оси цилиндра, чтобы усложнить каскейду задачу. Тот не пасует и выдает B-поверхность:
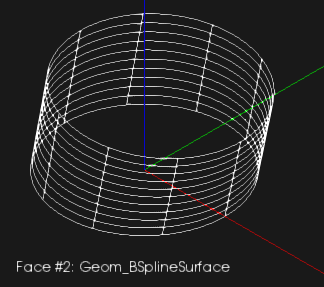
По правде говоря, в этом случае можно было обойтись и линейчатой поверхностью, т.е. лоскутом, соединяющим оба сечения сегментами прямых линий. OCCT не стал заморачиваться и выдал сплайновую геометрию. На самом деле, утилита BRepOffsetAPI_ThruSections предоставляет специальный флажок для включения режима линейчатых поверхностей. Мы не будем на этом останавливаться, а продолжим игру на большем количестве сечений.
Пробуем:
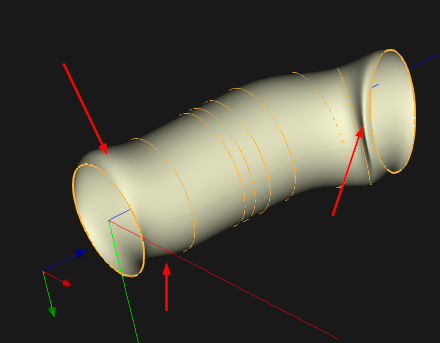
Результат получается, мягко говоря, «не очень». Даже на сечениях одинакового диаметра мы имеем множество осцилляций. При этом, добавляя сечение в конец трубки, мы рискуем испортить ее форму в начале, так как скиннинг — операция глобальная.
Для полноты картины зададим утолщение где-нибудь посередине трубки.

Ба-бах!

Утолщение получилось, но трубку нешуточно выдавило. Что ж, результат все еще математически корректен, хотя форма совершенно несносна. Вообще, конкретно этот алгоритм демонстрирует удивительное свойство, которое я бы назвал «раздражительностью». Скиннинг готов терпеть ваши сечения только до определенного момента. После добавления очередной кривой градус «раздражения» выходит за рамки разумного, и вот вы уже крутите в руках не модель, но математическую игрушку. Формально, повторюсь, абсолютно корректную.
Когда я впервые увидел этот результат, мне стало безвыходно ясно, что продолжать использовать скиннинг бессмысленно. Я даже сформулировал заповедь: «не используйте скиннинг для моделирования трубок с утолщениями, да и трубок вообще!». Но я ошибался.
Скиннинг PRO
Знающий человек смотрел мой код с использованием BRepOffsetAPI_ThruSections цокая языком, как бы говоря «ну кто же так делает». Ведь я не уделил совершенно никакого внимания настройке скиннера, то есть не инициализировал его должным образом. А правильно вот как (вместо одной строчки — три):
// Initialize and build BRepOffsetAPI_ThruSections ThruSections(0, 0, 1.0e-2); ThruSections.SetSmoothing(1); ThruSections.SetMaxDegree(5);
Пожалуй, основная модификация здесь — это включение режима «smooth» и ограничение степени результирующего сплайна. Знающий человек задумался на минуту над тем, какую степень использовать лучше всего. Мое предложение поставить число 3 (ведь нас еще в университете учили кубическим сплайнам) было отвергнуто сразу и с презрением. «Пять — лучше». Что ж, лучше значит лучше. Самое время повторить эксперимент. Подготовим нужные сечения сразу:
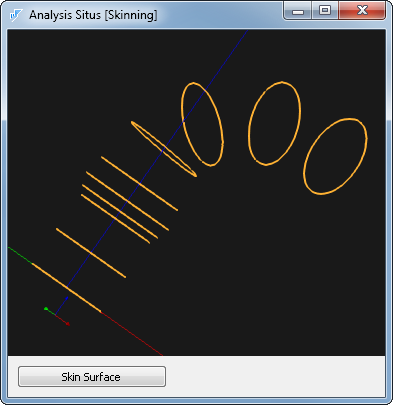
Ниже дана сводка по используемым сечениям. Tx, Ty, Tz — это смещения вдоль глобальных осей координат. Rx, Ry, Rz — это соответствующие углы поворота в радианах:
| Cечение | Радиус | Tx | Ty | Tz | Rx | Ry | Rz |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 2 | 0 | 0 | 0 |
| 4 | 1.1 | 0 | 0 | 2.2 | 0 | 0 | 0 |
| 5 | 1.2 | 0 | 0 | 2.5 | 0 | 0 | 0 |
| 6 | 1.1 | 0 | 0 | 3 | 0 | 0 | 0 |
| 7 | 1 | 0 | 0 | 4 | 0 | 0.1 | 0 |
| 8 | 1 | 0.5 | 0 | 5 | 0 | 0.8 | 0 |
| 9 | 1 | 2.2 | 0 | 6 | 0 | 1.3 | 0 |
| 10 | 1 | 4.2 | 0 | 6.2 | 0 | 1.55 | 0 |
Ничего хорошего я, признаюсь, увидеть не ожидал. Ведь на этих сечениях мною изначально был получен вот такой результат:
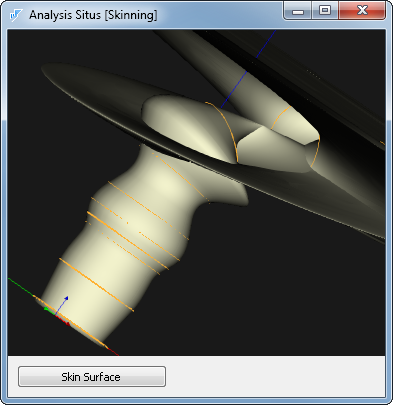
Вид из космоса:
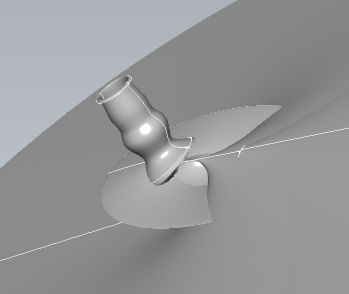
На приведенной картинке результирующая поверхность совершает какую-то чудовищную осцилляцию. Однако вот результат после модификации знающим человеком:
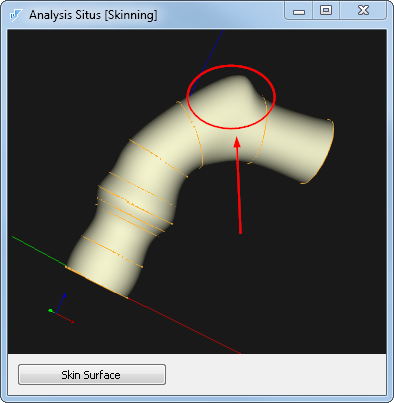
Это уже куда как лучше. Однако и здесь мы видим уродливый горб ближе к окончанию трубки. Вообще-то этот изъян по всей видимости можно вылечить путем добавления новых сечений. Но я поступил иначе. Когда знающий человек оказался достаточно далеко, я изменил степень 5 на 2, ведь более низкая степень делает полиномиальный «материал» менее податливым. И вот результат:
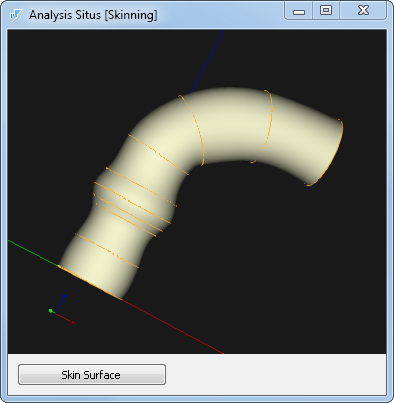
И поверхность весьма хороша:

Итак, скиннинг работает. Но в моделировании трубок это все-таки немного не тот способ, который следовало бы применять. Ведь в действительности, играя теми или иными его параметрами, мы все же слабо контролируем форму поверхности. Нам мало что известно о ее поведении между сечениями. Какому закону она подчиняется? Может быть есть более натуральный способ смоделировать трубку переменного радиуса? Такой же, например, как GeomFill_Pipe, только более гибкий...
В поисках API
OCCT — это такая огромная темная пещера с множеством ходов и мелких лазеек. Вы можете любоваться причудливыми сводами его Булевых Операций, не подозревая о том, что примерно такой же Sanctum так называемых «Старых Булевых» вознес свои более хрупкие колонны где-то неподалеку. В этой пещере нельзя включить свет. Отсюда миссия. Наш блог во многом является журналом путевых заметок: где повернуть, где пригнуть голову.
Найти подходящий API не так просто. Особенно, если заранее не знать, а существует ли он вообще. Мне помог блог Романа Лыгина. В нем дается исходный код решения, позволяющего строить трубки с переменным радиусом. Идея алгоритма довольно органично расширяет уже известный нам GeomFill_Pipe. Теперь мы указываем, что сечение вдоль кривой должно изменяться (например, скалироваться) сообразно некоторой функции, или «закону» (Law). Формально, закон задается как функция одного переменного — параметра вдоль траектории.
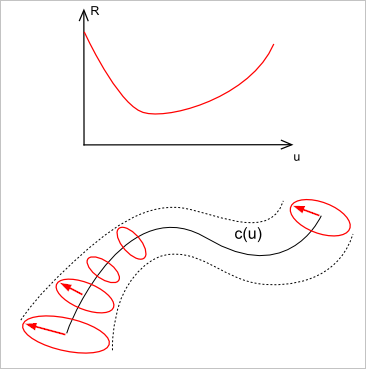
Для полноты картины приведем исходный код (немного видоизмененный код Романа) в виде команды для Draw (функция VariableSweep):
static Handle(Law_BSpFunc) CreateLawFunc(const Handle(Geom2d_BSplineCurve)& lawCurve,
const double f,
const double l)
{
//---------------------------------------------------------------------------
// Knots are recalculated from lawCurve to fit into [f, l] range
//---------------------------------------------------------------------------
const int nPoles = lawCurve->NbPoles();
TColgp_Array1OfPnt2d aPArrE(1, nPoles);
lawCurve->Poles(aPArrE);
TColStd_Array1OfReal aPArr(1, nPoles);
// Y coordinates of poles are used to build one-dimensional b-curve
for ( int i = 1; i <= nPoles; i++ )
aPArr(i) = aPArrE(i).Y();
const int nKknots = lawCurve->NbKnots();
TColStd_Array1OfReal aKArrE(1, nKknots), aKArr(1, nKknots);
lawCurve->Knots(aKArrE);
TColStd_Array1OfInteger aMArr(1, nKknots);
lawCurve->Multiplicities(aMArr);
// Redistribute knots
const double aKF = aKArrE(1), aKL = aKArrE(nKknots);
const double aKRatio = (l - f) / (aKL - aKF);
for ( int i = 1; i <= nKknots; i++ )
aKArr(i) = f + (aKArrE(i) - aKF) * aKRatio;
// Build B-spline law
Handle(Law_BSpline) aBs;
if ( lawCurve->IsRational() )
{
TColStd_Array1OfReal aWArrE(1, nPoles);
lawCurve->Weights(aWArrE);
aBs = new Law_BSpline( aPArr, aWArrE, aKArr, aMArr, lawCurve->Degree(), lawCurve->IsPeriodic() );
}
else
aBs = new Law_BSpline( aPArr, aKArr, aMArr, lawCurve->Degree(), lawCurve->IsPeriodic() );
return new Law_BSpFunc(aBs, f, l);
}
static int VariableSweep(Draw_Interpretor&, Standard_Integer, const char**)
{
//---------------------------------------------------------------------------
// Stage 1: we start with a Bezier path for fun
//---------------------------------------------------------------------------
TColgp_Array1OfPnt pathPoles(1, 4);
pathPoles(1) = gp_Pnt(0.0, 0.0, 0.0);
pathPoles(2) = gp_Pnt(50.0, 10.0, 0.0);
pathPoles(3) = gp_Pnt(70.0, 40.0, 0.0);
pathPoles(4) = gp_Pnt(150.0, 30.0, 0.0);
Handle(Geom_BezierCurve) path = new Geom_BezierCurve(pathPoles);
//
DrawTrSurf::Set("path", path);
//---------------------------------------------------------------------------
// Stage 2: build law. Y coordinates define the radius
//---------------------------------------------------------------------------
Handle(TColgp_HArray1OfPnt2d) law_pts = new TColgp_HArray1OfPnt2d(1, 3);
Handle(TColStd_HArray1OfReal) law_params = new TColStd_HArray1OfReal(1, 3);
//
gp_Pnt2d law_P1(0.0, 1), law_P2(0.5, 10), law_P3(1.0, 1);
law_pts->SetValue(1, law_P1);
law_pts->SetValue(2, law_P2);
law_pts->SetValue(3, law_P3);
//
law_params->SetValue(1, 0.0);
law_params->SetValue(2, 0.5);
law_params->SetValue(3, 1.0);
//
Geom2dAPI_Interpolate Interp( law_pts, law_params, 0, Precision::Confusion() );
Interp.Perform();
if ( !Interp.IsDone() )
{
std::cout << "Cannot build law curve" << std::endl;
return 1;
}
Handle(Geom2d_BSplineCurve) law_radius_curve = Interp.Curve();
//
DrawTrSurf::Set("evol", law_radius_curve);
//
Handle(Law_BSpFunc)
law = ::CreateLawFunc( law_radius_curve, path->FirstParameter(), path->LastParameter() );
//---------------------------------------------------------------------------
// Stage 3: now build sweep. X coordinates define the radius
//---------------------------------------------------------------------------
// Construction parameters
const double prec = 1.0e-6;
const GeomAbs_Shape continuity = GeomAbs_C2;
const int maxDegree = 25;
const int maxSegment = 1000;
// Circular profile
Handle(Geom_Circle) circProfile = new Geom_Circle( gp::XOY(), 1. );
DrawTrSurf::Set("profile", circProfile);
// Perpendicular section (Frenet makes it orthogonal)
Handle(GeomFill_SectionLaw) sectionLaw = new GeomFill_EvolvedSection(circProfile, law);
Handle(GeomFill_LocationLaw) locationLaw = new GeomFill_CurveAndTrihedron(new GeomFill_CorrectedFrenet);
Handle(GeomAdaptor_HCurve) pathAdt = new GeomAdaptor_HCurve(path);
locationLaw->SetCurve(pathAdt);
// Construct sweep
GeomFill_Sweep Sweep(locationLaw, 0);
Sweep.SetTolerance(prec);
Sweep.Build(sectionLaw, GeomFill_Location, continuity, maxDegree, maxSegment);
//
if ( !Sweep.IsDone() )
{
std::cout << "Error: cannot build evolved sweep" << std::endl;
return 1;
}
//---------------------------------------------------------------------------
// Stage 4: get the result
//---------------------------------------------------------------------------
Handle(Geom_Surface) S = Sweep.Surface();
const double err = Sweep.ErrorOnSurface();
DrawTrSurf::Set("surf", S);
std::cout << "Error: " << err << std::endl;
return 0;
}
На что здесь следует обратить внимание? Прежде всего, на функцию CreateLawFunc, которая нужна для задания закона изменения профиля. Однако сама эта функция закон не задает. Она всего-лишь извлекает его из немного хитрой формы, каковой является двумерная B-кривая. Эта кривая имеет в качестве ординаты значение радиуса, а ее абсцисса реально не используется (хотя мы и задали ее равной параметру вдоль траектории для удобства). Несмотря на некоторую избыточность, мы можем теперь визуализировать закон изменения радиуса в Draw:
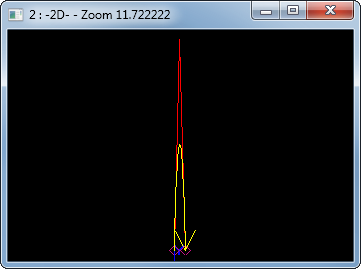
В данном примере радиус имеет пик посередине траектории. Результат моделирования представлен ниже:

Поверхность, как ожидалось, оказывается сплайном, причем весьма неплохого качества.

Вот и все
Вот так, дорогие товарищи программеры, инженеры и геометры. Этот урок построения трубок оказался неожиданно для меня увлекательным. И весьма характерным. Осваиваясь с новой библиотекой, не следует рубить с плеча. OCCT умеет много больше, чем можно было бы подумать. Вот только это сокровенное знание надо уметь извлекать. С одной стороны это, конечно, плохо. А с другой, OCCT — настоящая хакерская библиотека :).
Примечание: как работает скиннинг (BRepOffsetAPI_ThruSection)
Качественно иное поведение скиннера при включении «сглаживания» (smoothing) пробуждает интерес к тому, что же все-таки происходит там, внутри. Не вдаваясь в детали, отметим лишь общую идею алгоритма.
Сначала все сечения преобразуются к сплайновому представлению. Таким образом, наши окружности в реальности превращаются в сплайновые кривые. Насколько мне удалось понять, нерациональные (non-rational). Это выглядит немного странно, особенно, если добавить, что степень кривой получается высокой: 13. Возможно, в этом отношении алгоритм может быть доработан, надо смотреть.
Все сечения поступают на вход утилите GeomFill_SectionGenerator. Здесь они «причесываются» в соответствии с требованием классического алгоритма скиннинга о том, что опорные кривые должны быть согласованы. Согласование приводит к тому, что кривые получают одну и ту же степень (для сплайнов более низкого порядка степень повышается — degree elevation) и узловой вектор (идет вставка узлов — knot insertion).
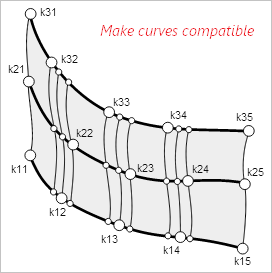
Наконец, «магия» творится инструментом GeomFill_AppSurf. Это и есть скиннер. В его вычислительной схеме реализована специальная ветвь на случай «сглаживания»: вызов аппроксимации AppDef_Variational. Это альтернатива аппроксимации при помощи класса AppDef_BSplineCompute, который используется, если «сглаживание» отключено. По сути мы имеем два абсолютно разных алгоритма. Надеюсь, в будущем нам представится возможность разобраться с ними подробнее.
2015-12-16 в 12:35:39
Читать Ваши статьи -- одно удовольствие. Конечно, это все нужно прорабатывать, но я засомневался во фразе "По сравнению с предыдущим случаем здесь налицо переменный радиус сечения вдоль траектории. Само сечение при этом остается круговым, т.е. симметрия трубки не нарушена (иначе это уже не трубка). Проблема перестает быть тривиальной. Утилита GeomFill_Pipe оказывается непригодной, нам нужен другой подход."
Вроде бы такая ситуация покрывается
GeomFill_Pipe (const Handle< Geom_Curve > &Path;, const TColGeom_SequenceOfCurve &NSections;)
Create a pipe with N sections. The section evoluate from First to Last Section
хотя нужно аккуратно попробовать.
Еще раз спасибо, особенно за две последние статьи. И еще, хотелось бы получить комментарий про GeomFill_TrihedronLaw. Что такое GeomFill_Frenet, что такое GeomFill_CorrectedFrenet?
2018-10-24 в 12:59:16
Не знаю как решить вопрос с построением вдоль траектории не имеющей скруглений. Я использую BRepOffsetAPI_MakePipe, но та же проблема присутствует в BRepFill_Pipe и BRepFill_PipeShell.
Если траектория не имеет скруглений, например, состоит из двух перпендикулярных линий имеющих общую точку, то OCCT перестает ориентировать нормаль профиля по траектории (далее приложу картинки). Одним из решений является создание скруглений в местах соединения прямых. Это хорошо обсудили тут: https://stackoverflow.com/questions/47163841/pythonocc-opencascade-create-pipe-along-straight-lines-through-points-profile/48491990
Но что, если мне нужен НЕ скругленный угол?!
Я хочу так: https://images2018.cnblogs.com/blog/534255/201804/534255-20180426211455845-1730615366.png
Но имею это: https://images2018.cnblogs.com/blog/534255/201804/534255-20180426211454207-1361314237.png
Как добиться такого результата? Я взял картинки из статьи в блоге (https://www.cnblogs.com/opencascade/p/8955053.html), но непонятно, как автор добился такого результата.
2018-10-25 в 21:10:50
В принципе авторы cn-блога дают рецепт такого моделирования. Они приводят скрипт Draw, состоящий из четырех команд:
1) mksweep: Инициализирует инструмент BRepOffsetAPI_MakePipeShell траекторией, по которой будет двигаться профиль.
2) addsweep: Инициализирует профиль (сечение), который будет двигаться вдоль траектории.
3) setsweep: Определяет эволюцию профиля в ходе его протягивания вдоль траектории. Ключ "FR" означает репер Френе.
4) buildsweep. Выполняет оператор. Ключ "C" предписывает обрабатывать стыки стратегией "Extend & Intersect".
Попробовал повторить в коде на простом профиле и траектории. Вроде получилось. Можете посмотреть код функции MISC_TestSweep1 на свалке экспериментальных команд: https://gitlab.com/ssv/AnalysisSitus/blob/master/src/cmdMisc/cmdMisc.cpp
Картинка: http://quaoar.su/imgs/blog/test-sweep1.png
2018-11-01 в 15:37:48
А есть способ получить призму по профилю со "спиленными" под углом концами? Т.е. грубо средний сегмент трубы из картинки http://quaoar.su/imgs/blog/test-sweep1.png без первого и третьего.
2018-11-01 в 16:35:50
Если сечение трубки не должно быть круговым, то самый простой способ -- протянуть призму из "косого" сечения, например, так:
Код функции MISC_TestSweep2: https://gitlab.com/ssv/AnalysisSitus/blob/master/src/cmdMisc/cmdMisc.cpp#L1079
Результат: http://quaoar.su/imgs/blog/test-sweep2.png
Или способ "в лоб": строим трубку с ортогонально нанизанным сечением, после чего отсекаем хвосты булевой операцией для формирования нужных скосов.