On the recognition of threads in CAD models

Feature recognition on CAD models is a tough topic. This is where Analysis Situs finds its niche thanks to the availability of basic shape interrogation and matching algorithms. There are different feature types and different application areas for feature recognition, including, but not limited to:

1. NC paths generation.
2. Manufacturability analysis.
3. Direct editing of CAD models.
4. CAD model simplification and idealization for numerical simulations (CAE).

The common ground for these application areas is the ability to extract as much semantics from a dumb geometry as possible. While the foundation classes of Analysis Situs are well-proven (they have been used to develop a bunch of commercial-grade software), the entire feature recognition business cries for customization. It seems to be nearly impossible to modularize the recognition algorithms in a sort of a library that would serve all the niches equally well. Features are different, and their taxonomy would vary depending on the perspective you put on them.

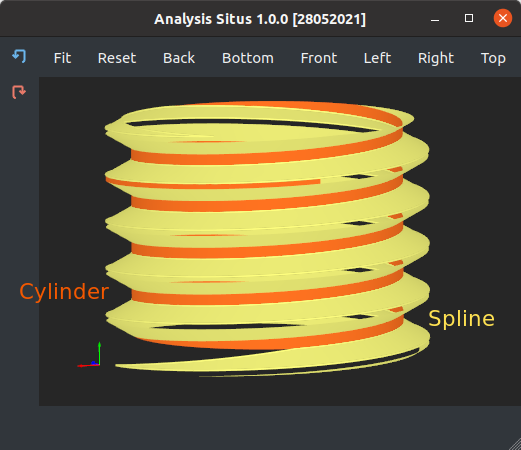Splines and cylinders constituting a typical thread feature.

Today let's speak about the recognition of threads. Thread is a feature often found in the milled and turned parts. Threads can be applied to any internal or external cylindrical face, and that is why they leave a portion of the original cylinder as a hint. As usual, an accurate threads recognition requires selecting strong geometric heuristics, such as:

1. There should be a set of spline surfaces making up the angled thread flanks (see the hand-made illustration down below).
2. The surfaces are kind of helical, i.e., they have "support" edges lying on a couple of cylinders: the major and the minor ones.
3. The radii of those cylinders should differ just slightly.
4. If one takes the osculating circles of the helical splines, their centers of curvature should coincide with the bore axis (the axes of the major and minor cylinders extracted beforehand).
5. The thread's edges could be fit with a helical curve with some standard parameters (e.g., check out the Unified Thread Standard).

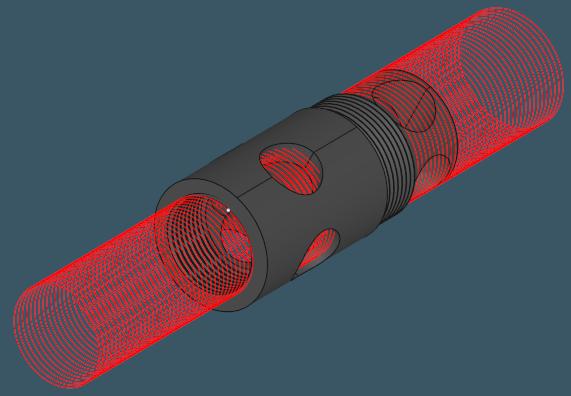Helix splines fitting into the threads for extracting pitch values.

The recognition process can be based on the Recognizer/Rule interplay that is the architectural pattern with proven capabilities of extracting well-formalized features. The careful explanation of the recognition logic will bring us too deep into the algorithmic details, and that is unlikely a good fit for blogging. Let me rather share some interesting discoveries that I made for myself in the course of implementation. The topics outlined below can serve as a good start for the follow-up blogs. Additionally, these notes would hopefully allow us to discuss some typical challenges in the thread recognition problem specifically and feature detection in general.

A cylinder from a point tuple

Looking for a cylinder fitting procedure, I came across the paper [Lichtblau, D. (2012). Cylinders Through Five Points: Computational Algebra and Geometry. Journal of Mathematics Research, 4(6)]. This paper brings up an elegant mathematical formulation for the cylinder fitting problem. Given five points on a helical curve (remember that we are recognizing helix-like threads), one could generate a set of cylinders passing through these points by solving a system of polynomial equations. Long story short, all my attempts to attack this problem with OpenCascade's math_FunctionSetRoot and alike tools were desperate. Hopefully, I will find time in the future to run it all in MATLAB (or any other well-proven math system) and check whether it's my fault or something. If there's anything exciting in there, we will come back to this topic in the future.

Analytics and standards

Searching for the thread pitch (the distance between thread peaks), it's no surprise to discover a sort of a helical path followed by the corresponding CAD edges. Sometimes, fitting an analytical and parametric entity is an elegant solution for extracting unknown feature properties. Fitting an analytical primitive is a way to attach explicit design intent to a speechless CAD part.

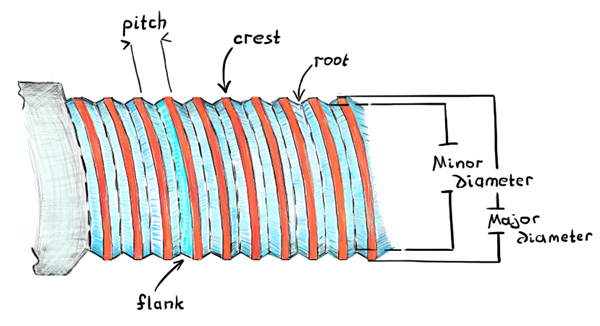Thread's subfeatures.

In fact, features are rarely random. Speaking about thread recognition, we are not solving a purely geometric problem, because all thread pitches are sort of standard. Therefore, if you happened to extract the pitch value of 0.961 mm, check it closely again. Make sure that it's not rather the standard 1.0 mm pitch that your numerical method failed to snap to. The design intention should always be kept on your mental radar. You might even want to have a resource file with a catalog of features and their allowed dimensions.

Do not go gentle evaluate osculating circles at B-spline knots

Simply do not do that. Here's a youtube video demonstrating how weird the results could be (and be informed before you jump into watching it: my wife told me it's impossible to understand). Also bear in mind that this numerical methods business is never numerically perfect.

The Method

Any geometry processing algorithm is not something as elegant as Bubble Sort if you know what I mean. The data is never perfect and the number of possible CAD variations could easily burn quite some brain cells, leaving you as a sorry idiot incapable of understanding your own code. Someone said that debugging requires twice the brainpower that one spends on developing. Therefore, if you did your best to develop, you will not be able to debug the thing. Ta-dam.

Outer thread on a chess rook (green).

Still, I have The Method for you. It is actually not my invention and it may sound stupidly simple, but here it is anyway. I could not name it as a documentation-driven or test-driven development method, because it's a mix of both. Here is just a handful of rules to follow:

• Start with a single-page memo explaining the core idea of the algorithm. The idea should be really sound, and if you are using any heuristics, they should all be as strong as possible. This is where common sense is often enough. And make sure to discuss it with somebody who cares once you wrote it down.


• Collect input data and make sure to establish a non-regression testing system for your algorithm. Without tests, you're blind and cannot experiment with the data, logic, and heuristics.


• Get back to your memo and add there a section like "TODO." In this section, you're going to put everything that comes into your mind as long as you're working on the algorithm. And by "everything" I mean all sorts of thoughts, ideas, and discoveries ranging from "discuss this and that with Carl" and ending up with the listing of problematic cases you were able to identify. Make sure to keep the TODO section up-to-date.


• Your algorithm is close to completion when most of the checkboxes in the TODO section are clicked on. For the tricky ones, you might want to create separate tickets in your Jira.

It's all trivial but I can say for sure that most people do not bother themselves with The Method and prefer something more brutal, like "do or die; no pain no gain; go hard or go home." A good algorithm takes time to develop, and you need a framework of thought that would allow you to organize your thinking process and write down all the questions branching out in your head (there would be so many that you'll never manage to memorize them).

Want to discuss this? Jump in to our forum.