Исследование двугранного угла
В некоторых задачах геометрического моделирования требуется проанализировать ребра модели на предмет их выпуклости / вогнутости. Рассмотрим типичную B-Rep модель, полагая для простоты, что все ее грани планарны. Проверка выпуклости стыка между гранями есть не что иное, как проверка выпуклости ребра. Чтобы ее осуществить, будем опираться на топологические свойства модели.
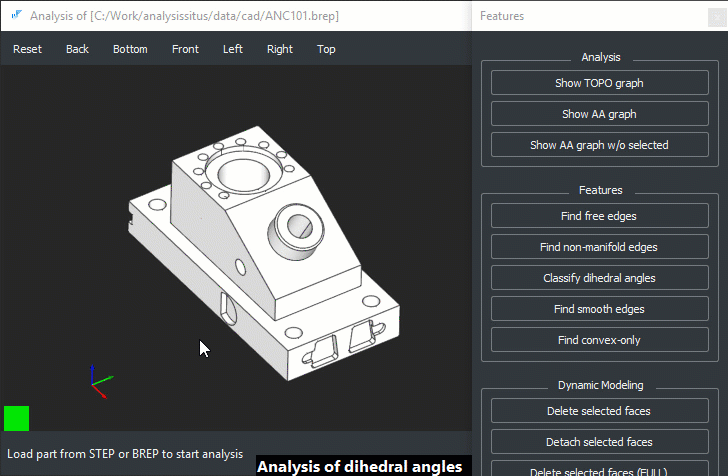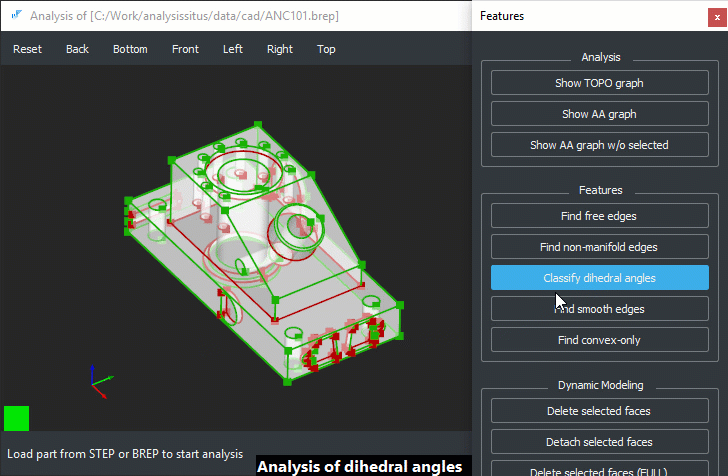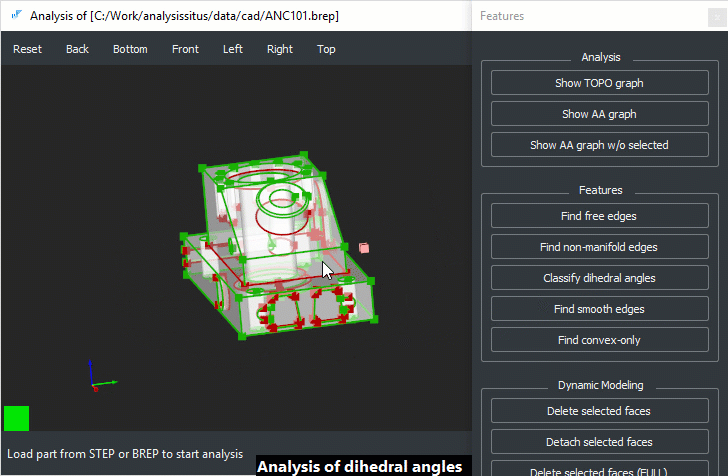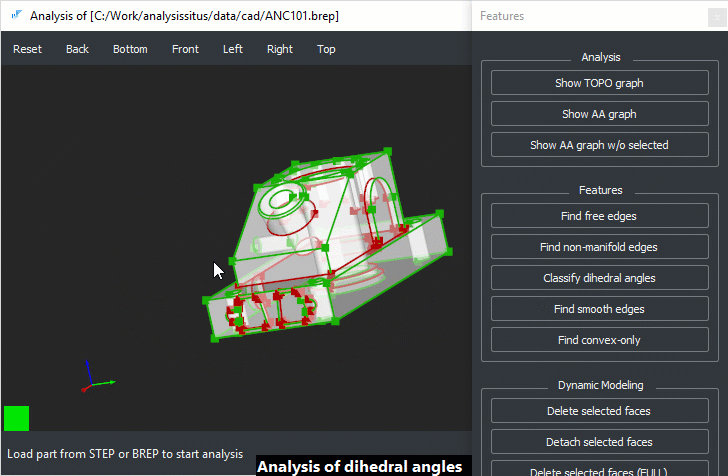
Ориентация
Граничному представлению тела присуще то свойство, что внешний контур всякой грани обходится против часовой стрелки, если смотреть на него со стороны нормали к поверхности (рис. 1).
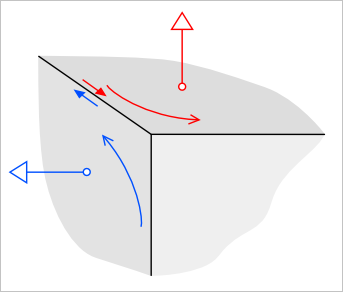
Рис. 1. Две смежные грани твердотельного объекта и их ориентации.
Сделаем по этому поводу несколько важных замечаний, которые не станут откровением для внимательных читателей данного блога.
- Направление обхода — это так называемая ориентация контура.
- Направление нормали — это ориентация грани.
- Ориентация бывает геометрической и топологической. Геометрическая ориентация полностью определяется математической формулой задания геометрии (рис. 2). Мы не желаем ее изменять, так как это повлекло бы изменение геометрии модели.
- Топологическая ориентация — это геометрическая ориентация плюс специальный флаг, с помощью которого мы можем геометрическую ориентацию обратить. По сути этот флаг выражает наше согласие или несогласие с геометрически детерминированной ориентацией.
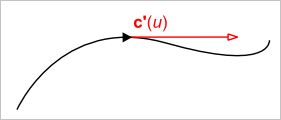
Рис. 2. Геометрическая ориентация кривой.
Итак, есть две ориентации: геометрическая и топологическая. Вернемся теперь к правилу обхода внешнего контура. Повторим это правило:
Используя наше знание об ориентациях, переформулируем:
Имея в виду это правило, мы можем эффективно жонглировать векторами ориентации контура и грани, тем самым привлекая методы простейшего векторного анализа для решения многих задач. В частности, знание о том, куда смотрят или должны смотреть векторы, связанные с ребром или гранью, помогают исследовать тело «в малом», а именно выяснять, с какой стороны содержится ограничиваемый телом объем и в каком количестве. Именно количество объема в малом для многообразной (2-manifold) геометрии дает нам представление о качестве двугранного угла: выпуклый он или вогнутый.
Проверка выпуклости
Возьмем две смежные грани F и G. Если эти грани были изъяты из корректно построенного твердого тела, то они сохраняют информацию о смежности на уровне структур данных. А именно, есть набор ребер (в простейшем случае одно ребро), принадлежащий обеим граням, и эту информацию можно извлечь. Ниже приведен кусочек кода для сбора всех ребер граней F и G (библиотека OpenCascade).
... // Extract edges for faces TopTools_IndexedMapOfShape EdgesF, EdgesG; TopExp::MapShapes(F, TopAbs_EDGE, EdgesF); TopExp::MapShapes(G, TopAbs_EDGE, EdgesG);
Данный код собирает два множества ребер (EdgesF и EdgesG) при помощи метода MapShapes() пакета TopExp (topology exploration). Выражаясь теоретико-множественным языком, эти два набора ребер нужно пересечь, то есть взять их общую часть. Сделать это можно, например, вот так:
...
// Collect common edges
TopTools_IndexedMapOfShape commonEdges;
TopoDS_Edge commonEdge;
for ( int ef = 1; ef <= EdgesF.Extent(); ++ef )
{
for ( int eg = 1; eg <= EdgesG.Extent(); ++eg )
{
if ( EdgesF(ef).IsSame( EdgesG(eg) ) )
{
commonEdges.Add(EdgesF(ef));
//
if ( commonEdge.IsNull() ) // A single common edge is enough for analysis
commonEdge = TopoDS::Edge( EdgesF(ef) );
}
}
}
Обратим внимание на проверку двух ребер методом IsSame(). Такая проверка не различает ОРИЕНТАЦИЮ ребра, то есть она распознает два вхождения одного ребра в смежные грани как одинаковые. После выполнения приведенного кода коллекция commonEdges содержит только общие ребра. Для анализа двугранного угла все смежные ребра нам не нужны, достаточно одного. Это произвольное ребро было сохранено в переменной commonEdge. Подчеркнем, что речь идет об одном ребре, имеющем два вхождения в смежные грани. При этом форма ребра в пространстве моделирования задается единственной параметрической кривой c(u), имеющей собственную ГЕОМЕТРИЧЕСКУЮ ориентацию (черная стрелка на рис. 3).
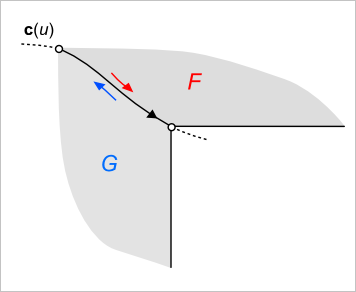
Рис. 3. Ребро имеет два вхождения и одну пространственную кривую.
На данном ребре мы выберем две точки так, чтобы они шли вслед друг за другом с учетом ориентации контура. Для этого возьмем на кривой две точки A и B (рис. 4), не уточняя заранее, какая из них считается первой, а какая второй. Упорядочить эти точки можно лишь относительно того контура, который мы рассматриваем (то есть порядок различен для граней F и G).
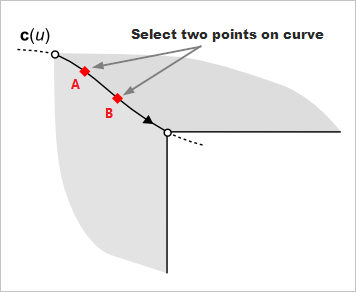
Рис. 4. Выбираем две произвольные точки на кривой.
Пример кода для выбора точек на кривой приведен ниже:
... // Get host (shared) curve double f, l; Handle(Geom_Curve) probeCurve = BRep_Tool::Curve(commonEdge, f, l); // Pick up two points on the curve const double midParam = (f + l)*0.5; const double paramStep = (l - f)*0.1; const double A_param = midParam - paramStep; const double B_param = midParam + paramStep; // gp_Pnt A = probeCurve->Value(A_param); gp_Pnt B = probeCurve->Value(B_param);
Идея проверки выпуклости заключается в следующем. Проведя через опорные точки A и B вектор Vx, и указав вектор нормали Vz, мы построим для каждой грани характеристический трехгранник (Vx, Vy, Vz). Недостающая третья ось Vy этого локального репера окажется направленной по поверхности грани ВОВНУТРЬ, если восстановить ее как векторное произведение между нормалью Vz и вектором ребра Vx (порядок имеет значение). Угол между двумя такими осями дает искомый двугранный угол (рис. 5).
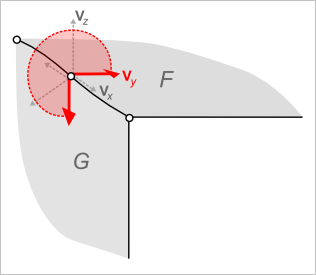
Рис. 5. Выпуклый двугранный угол.
Внимательный читатель заметит, что для правильного измерения двугранного угла требуется дополнительная референтная ось, в качестве которой можно взять вектор Vx для грани F. В результате, глядя со стороны референтной оси, искомый поворот от F к G будет совершаться против часовой стрелки.
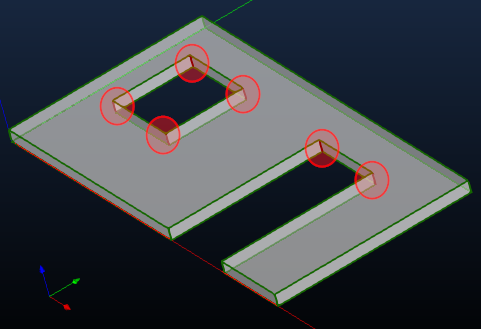
Рис. 6. Вогнутые (красный цвет, обведены) и выпуклые (зеленый цвет) двугранные углы на примитивной модели.
На рис. 6 показан результат классификации двугранных углов на простейшей модели, состоящей исключительно из планарных граней.
Криволинейные грани
Если грани вашего тела не планарны, то надо учесть некоторые нюансы. Прежде всего, опорные векторы надо конструировать локально из точки A. Кроме того, если угол между осями Vy обеих граней равен 180 градусам (что характерно для гладких сопряжений), то проверка угла может дать как положительное, так и отрицательное значение (рис. 7).
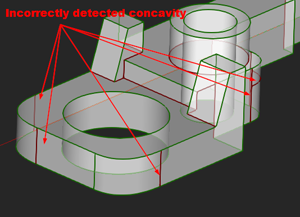
Рис. 7. Неверная и неустойчивая классификация на гладких сопряжениях.
Примитивное решение — отступить немного вдоль осей Vy для каждой грани, построить новые векторы и снова подсчитать угол. Шаг отступа при этом имеет смысл сообразовать с кривизной опорной поверхности. Такой подход уже годится для более-менее стандартных машиностроительных деталей (рис. 8).
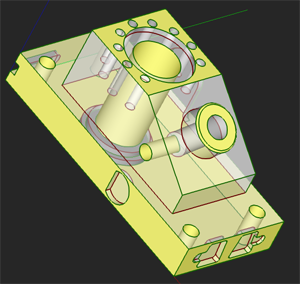
Рис. 8. Правильно классифицированные выпуклые и вогнутые ребра. Желтым подсвечены грани, все ребра которых выпуклы.
Заключение
Мы рассмотрели задачу измерения двугранного угла между гранями B-Rep модели. Эта функциональность востребована, прежде всего, в задачах распознавания конструктивных элементов модели (фичеров), о чем мы уже говорили в заметке о топологии САПР. В контексте механообработки выяснение, какая часть модели является отверстием, какая карманом и т.д. — важная составляющая процесса планирования производства. Эта задача может решаться по-разному, о чем мы еще поговорим в будущем. Атрибуция же ребер модели согласно признаку их выпуклости — один из базовых подходов, привлекаемых к решению данной задачи.