Sheet metal

1. Part 1 gives an introduction to unfolding and reviews the software packages solving similar tasks.
2. Part 2 explains how bends can be unrolled precisely.
3. Part 3 instructs how to survive the K-factor.
4. Part 4 outlines the structure of the unfolding algorithm. It also introduces the notions of "unfolding tree" and the "border trihedron" that are essential ingredients of the solution.
5. Part 5 introduces a generalized unfolding algorithm that can handle rolled parts and parts with specific design issues, such as terminating or consecutive bends.

Motivation

In this chapter, we discuss another challenging problem in sheet metal computations which is the prediction of bending sequence. Such an extension would allow us to guess the setups required to fabricate a part on a press brake, although we are not going to end up with a detailed manufacturing plan (at least, not yet). What is required for process planning is to know the restrictions on tools and bend lengths, i.e. the following questions have to be answered:

• Can we find a bend sequence where all bends are accessible by a punch?
• How many different punches are required and which geometry should they have?

Bending process starts with a flat workpiece and ends up with a folded state of the part. Bending operations are executed using various tools and holders, whereas tools consist of dies and punches of different shape and length. Tool selection and bend sequencing is driven, first of all, by geometric considerations. Our goal is to avoid interferences between the workpiece, the tool and the machine, although there are some other factors to take into account, such as tolerances, ergonomics, etc. All the latter issues we leave out of scope and stay focused on the geometric side of this entire business.

Sheet metal folding

To test a bend sequence, we have to be able to fold a flat pattern back while checking the feasibility of each successive fold. Therefore, we need to have a geometric algorithm to reverse unfolding. Let's briefly discuss some of the possible approaches, not diving too deeply in the implementation details.

Variant 1: Origami

One particularly simple way of folding consists in reimprinting the fold lines onto the flat pattern and rotating the left and right flanges by the half bend angle.

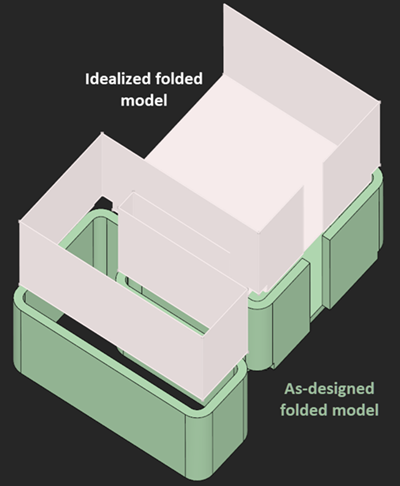(Over)Simplified folded model.

That's of course a lossy way of folding as it ignores material deformations and consequently does not revert the effects we modeled by introducing K-factor back in the days. Still, we consider such "origami" models as viable idealizations because the obtained folded models are often accurate enough to analyze bend sequence feasibility. There are many other unknowns to bending simulation, e.g., the geometric properties of punches themselves. Therefore, making the folded shapes of a workpiece as accurate as possible would not be enough for accurate simulation anyways.

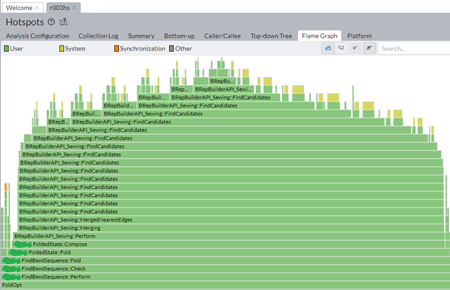Performance hotspot due to modeling overheads in one of extreme cases.

What you might expect from an "origami"-like approach is its inherent simplicity and, as a consequence, high performance of such a folding algorithm. In practice, though, simple resulting geometry does not necessarily mean speedy computations. The picture above illustrates an extreme case where the sewing operator (aimed at recovering the workpiece topology) takes forever to finish. Ideally, we wouldn't want to recover topology after each folding operation simply because folding is a homeomorphism. I.e., the topology of a part does not change from folding to folding and should be preserved at the level of the corresponding data structure.

Variant 2: Unfolding graph

A better approach to folding would be reusing the existing topology of a flat pattern that becomes available after unfolding. Reusing topology would allow us to escape from expensive modeling operations, such as edge imprinting and sewing (face stitching). We might come back to this idea in the future series.

Folding angle

In the [direct] unfolding algorithm, we used "border trihedrons" computed at face coedges to measure bend angles. In the reversed folding operation we can take advantage of the same exact apparatus. Once a part is unfolded, we get the information about the bend angles as the [angle, direction] pairs. The "direction" qualifier is either UP or DOWN depending on whether the corresponding flange comes up (elevates) or goes down with respect to a chosen side of a workpiece.

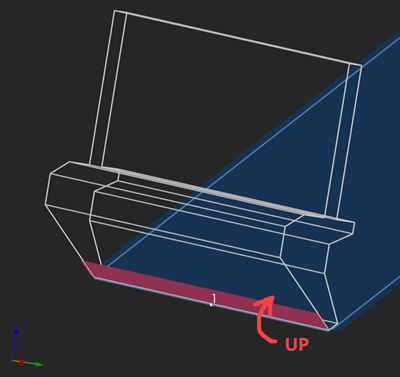UP bending direction.

To be able to distinguish between UP and DOWN directions, we should take into account the orientations of faces. Throughout the folding process, the orientations of faces (those "forward" vs "reversed" enums of OpenCascade) should be kept constant as otherwise their corresponding border trihedrons might get flipped.

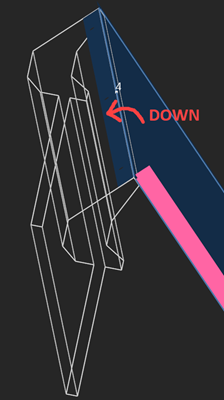DOWN bending direction.

The DOWN bending direction is a rotation around the local $\textbf{V}_x$ axis when the $\textbf{V}_z$ axes of the neighboring faces come outwards each other. The UP direction is the opposite: the $\textbf{V}_z$ axes of the border trihedrons rotate towards each other.

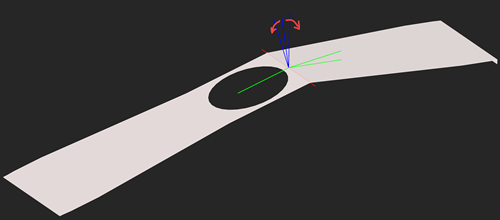Rotating border trihedrons.

The clip below shows a sequence of folding steps to make an "origami" shape. Here we are looking at subsequent intermediate folded states of geometry and not at the bending process as such. If you're seeking a realistic simulation (like in OSH Cut), you'll need to interpolate those folded states.

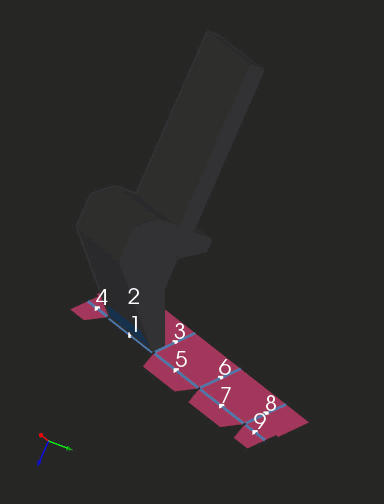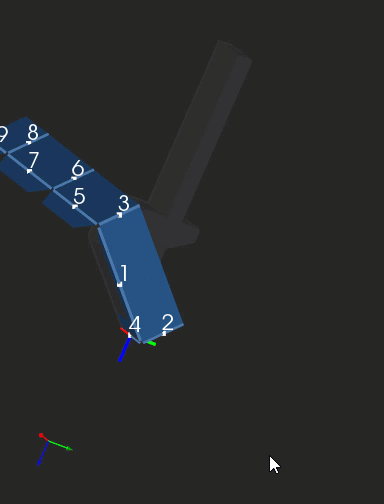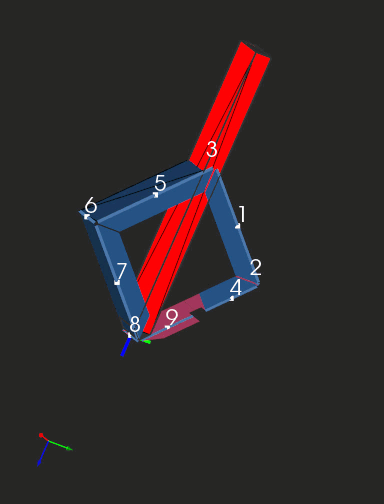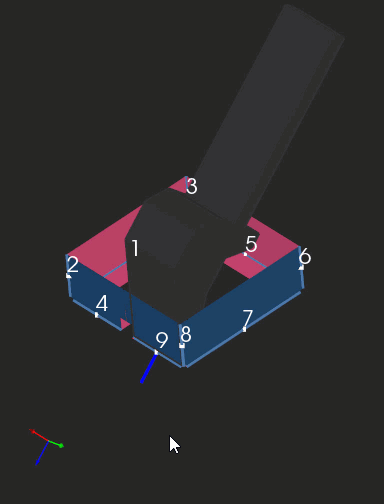Folding sequence with collision detection.

Tooling

Sheet metal bending is a process in which bends are formed using a combination of a punch and a die. Tool shapes should be such that there is no tool-part interference. Therefore, if we wanna simulate the process, each bending op has to be verified by a collision checker.

In their paper from 2001, U. Alva and S.K. Gupta describe how to build parametric models of punches for bending multiple parts in a single setup. They come up with the following criteria for a punch shape:

1. Compatibility with bend geometry: The punch radius should be compatible with the inside radius of the bend. The angle of the punch should be smaller than the bend angle.
2. Punch strength: The punch should be strong enough to withstand the bending forces.
3. Interference: The shape of punch should be such that there is no part-tool interference between the punch and any intermediate workpiece shape.

In what follows, we presume that a manufacturer has a variety of punches on hand and will not design a new punch to tackle an incoming sheet metal design. That is a reasonable assumption for mass-market products. Furthermore, punch strength is irrelevant as long as these punches exist and are happily employed in production.

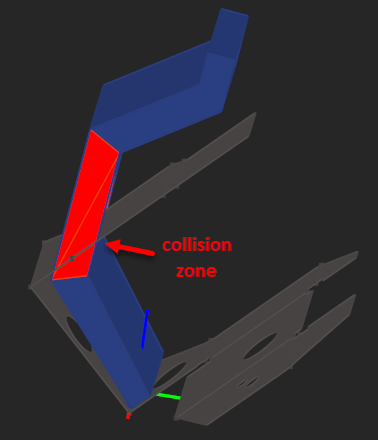Collision zone between a gooseneck punch and a sheet metal origami.

Punches should be chosen based on the sheet metal's geometry. Not every punch can fit into the next folded state of geometry obtained after the previous folds. That is the real difficulty, because a manufacturer must choose a manufacturing plan based on available facilities rather than abstract theoretical geometry.

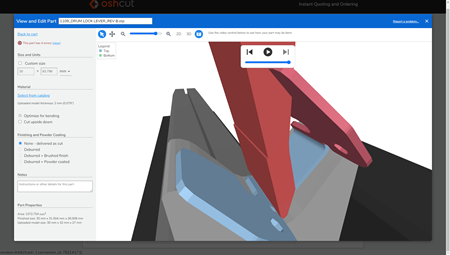Bending simulation in OSH Cut.

From the algorithmic perspective, we need a modeling "subsystem" responsible for generating tool punches and providing them to the collision checker. This can be a dictionary of tools or a simple parametric modeling function giving out punch solids for each bend being processed. The punch tools are simple prismatic shapes that can be easily constructed with OpenCascade modeling API.

Collision detection

Inexact collision checking approaches should be preferred when looking for a performant solution for bend sequence simulation. It is not even necessary to return the contact zone between the colliding solids. The collision checker must detect the hitting situation and return a Boolean flag as a result. A quick and reliable collision checker can be easily developed on top of OpenCascade's meshes, but we'll cover that in a later series.

Search space

Folding, punch modeling and collision checking are the essential algorithms that make bend sequence prediction possible. Nonetheless, they are insufficient. We still need to automatically choose the best folding sequence representing a sensible manufacturing plan. Assuming that all bends are enumerated like [1, 2, 3, 4, ... n], we would end up with at least $\mathcal{O}(n!)$ permutations (not taking into account flat pattern flipping). Checking them all is a desperate exercise, and that is why even professional simulation packages tend to search for a "good enough" suboptimal solution (or let you, as a user, hit a somewhat "Enough!" button). Let's take a look at how to browse this combinatorial space of variants.

Duflou's TSP

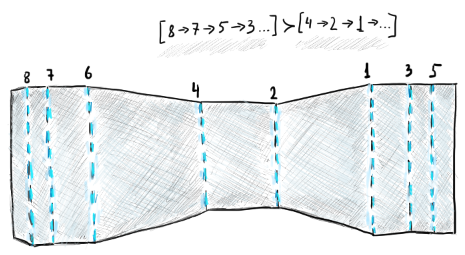Shape-determining bends are to be done after smaller-flange bends.

In the figure above, we have a flat pattern with all bend lines numbered. One pragmatic observation reflecting the manufacturing reality is that smaller flanges are often done before the larger ones (hence the "better" relationship between the two sequences in the figure). Duflou et al. (1999) come up with a bunch of empirical heuristics that are supposed to speed up finding better bend sequences.

In his paper, Duflou proposes two types of constraints: "hard" and "heuristic." By a "hard" constraint $a_{ij}$, he means that the bend $i$ should always be done before the bend $j$. The "heuristic" constraints are based on the empiric observations that formalize the process planner's experience.

The optimization technique adopted by Duflou is graph-based, assuming that the precedence relationships between bends are naturally turned into graph links. The graph nodes represent the folded states of geometry. It is quite evident that different bend sequences can bring us to the same state of folded geometry (at least, that would necessarily happen at the end), and that is why we have a graph and not a tree.

Furthermore, each graph link (i.e., folding operation) has its inherent "cost" value, and Duflou states that such a value should not be static. According to him, a "good cost estimate can only be made based on the knowledge of all previously passed nodes in the path under construction, and thus needs to be calculated dynamically during the search procedure." Duflou formulates this combinatorial optimization problem as TSP (traveling salesperson problem) and proceeds with a somewhat formal algorithm to solve it in an abstract way. In his formalism, all constraints are turned into numerical weights that are used to populate a penalty matrix being recomputed for each intermediate state of a workpiece.

This TSP-driven approach looks appealing due to its generality, although it remains completely unclear how good the approach is, given that there is no public implementation of this algorithm to test out. It is therefore even more appealing to stick to a somewhat stupidest possible approach based on blind permutations and gain some more experience on why it is actually such a bad idea.

Stupid simple → wise?

So, we know that a bend sequence like [1, 2, 3, ...] is unlikely an optimal solution as well as all its blind permutations. Now, here is the idea:

1. Let's assign some weights to each bend using the manufacturing-based heuristics.
2. Let's NOT sum up those weights into one meaningless "penalty" number.
3. Let's introduce not only absolute, but also relative weights to express that the applicability of one bend might depend on the preceding bends.
4. Finally, let's use all these weights to permute bend sequences in a somewhat intelligent way.

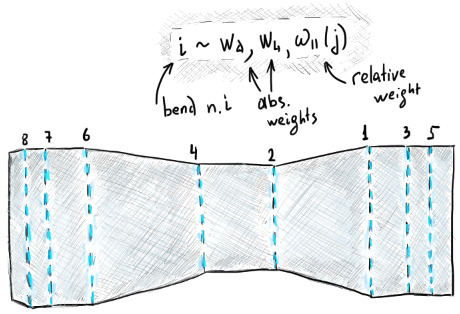Each bend might be associated with a weight or several weights.

The image above illustrates one possible suite of bend weights:

1. $w_d$ is the absolute weight associated with the distance from a bend line to the bounding rectangle of the flat pattern. This distance indicates how influencing this bend is w.r.t. the overall shape of the workpiece.
2. $w_l$ is the absolute weight associated with the bend length. According to Duflou, longer bends are preferably formed after significantly shorter ones.
3. $\omega$ is the relative weight such that $\omega_i(j) = 1$ if the $j$-th bend is parallel to the $i$-th one and zero otherwise.

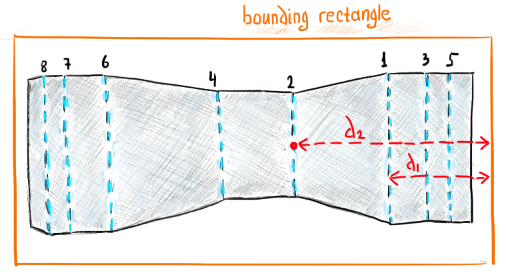The distance to the bounding rectangle is a measure of shape influence encoded by the weight $w_d$.

Now, having these weights, we can formulate the corresponding suite of permutation operators:

1. $P_w$ sorts the given sequence by descending absolute weights (global permutation).
2. $P_{\omega}$ permutes the given sequence by making sure that parallel bends follow each other (local permutation).
3. $P_{w + \xi}$ does that same thing as $P_w$ but adds small random perturbations $\xi$ to the used weights (global permutation).
4. $P_s$ is a global blind shuffle applied to the given sequence.

Combining those operators and applying them one after another in different ways, we can end up with a permutation strategy. This idea is attractive due to its inherent simplicity, although it obviously lacks any provable convergence properties and looks like a typical "engineering" solution: stupid and simple.

For example, why not using the following strategy?

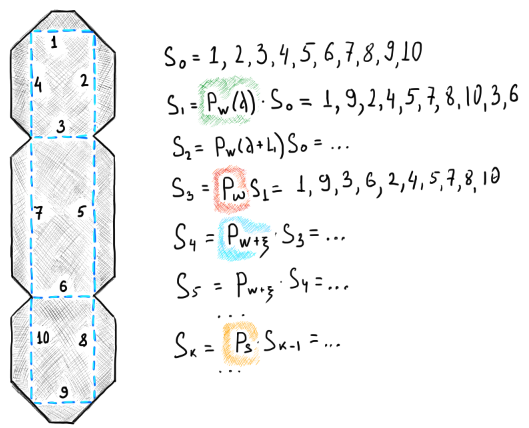Sequence permutation strategy based on 4 types of permutation operators (highlighted).

Let's comment a bit on this image. We start with sorting all bends by their absolute weights using the distance criterion: $P_w(d)$. Then, we add the bend length criterion by simply summing it up with the distance weight: $P_w(d + l)$. Next, using the $P_{\omega}$ operator, we enforce parallel bends go one after other. If this does not work out well, we apply random perturbations $P_{w + \xi}$ to the global weights and do several (how many?) iterations like this. After that, if nothing worked, we start to randomly shuffle bend IDs in the hope to cover the search space in a more uniform way and find a feasible solution: $P_s$.

From the architectural point of view, it makes sense to derive all permutation operators from a single base class and arrange the permutation strategy using the virtual functions of the base operator. This way, our computation would not end up limited with the prescribed suite of operators and we would be able to add more constraints and new types of weights later on.

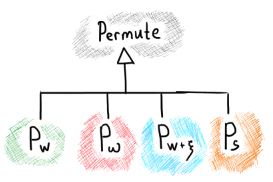Permutation operators (highlighted) can subclass the same base class.

Of course, permutations are blind, and it is unclear whether there is a practical method for using them wisely. Nevertheless, if you can make the entire computation as fast as possible you may conduct many more permutations and explore the search space in greater depth. Then, if there is still no solution after, say, 500 iterations, the tested design is probably suspicious and can be questioned by a human.

Want to discuss this? Jump in to our forum.