Sheet metal

1. Part 1 gives an introduction to unfolding and reviews the software packages for solving similar tasks.
2. Part 2 explains how bends can be unrolled precisely.
3. Part 3 instructs how to survive the K-factor.
4. Part 4 outlines the structure of the unfolding algorithm. It also introduces the notions of the "unfolding tree" and the "border trihedron" which are essential ingredients of the solution.
5. Part 5 introduces a generalized unfolding algorithm that can handle rolled parts and parts with specific design issues, such as terminating or consecutive bends.
6. Part 6 is the introduction to another challenging problem of sheet metal processing, which is bend sequence simulation.
7. Part 7 explains how to properly insert machined holes into a flat pattern.

Motivation

Is this a tube or a rolled sheet metal part?

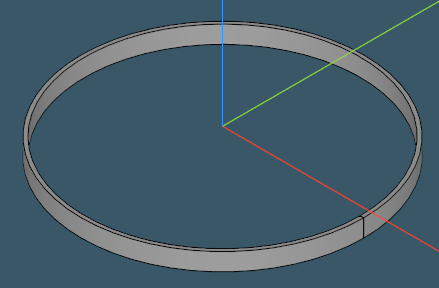And this?

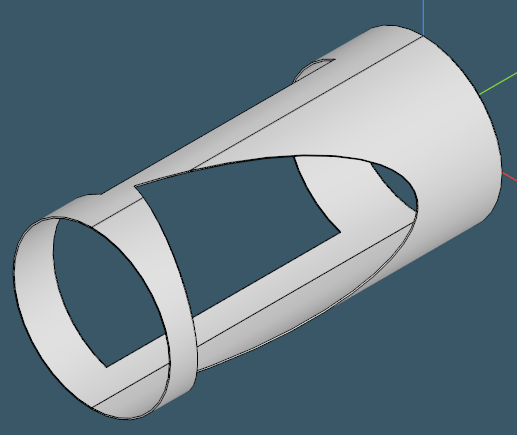Well, it can be both.

Struggling with edge cases is a particularly frustrating aspect of feature recognition algorithmization. At the same time, adding more and more specialized treatment to the recognition system improves the overall maturity of the computation. Ten years after we briefly discussed the "ecosystem" aspect of computing software, I'm more sure than ever that this metaphor turned out to be useful. Educating the algorithm to handle edge cases comes with the desire to keep the calculation structure tidy and straightforward, which is not always possible. That is why it is especially important to inject such improvements carefully and leave them sufficiently documented in the code.

So what makes a rolled part so different from a round tube, given that they sometimes have just about the same look? The distinction is the topology. A rolled part can be unfolded without adding extra cuts, while a tube is fundamentally closed. If we get rid of all inner features, then it will be safe to say that genus of a rolled part is 0, while for a tube it is essentially 1.

Let's discuss some of the computational approaches to detecting the unfoldability property of a round tube. Unfoldability requires the input part to have a border because we cannot flatten out a closed cylinder without making a cut. If there is such a seam cut, we may no longer recognize the object as a tube and should instead favor the rolled sheet metal type.

Search for angular gaps

A simple way to identify the presence of a border cut is to check whether the spanned angle of all consecutively rolled flanges is below 360 degrees.

In the engine room, we can examine the parametric domain of all cylindrical surfaces and sum up their U-ranges, which correspond to angular dimensions in OpenCascade's parameterization.

We use the same approach as one of the heuristics in the drilled hole recognizer.

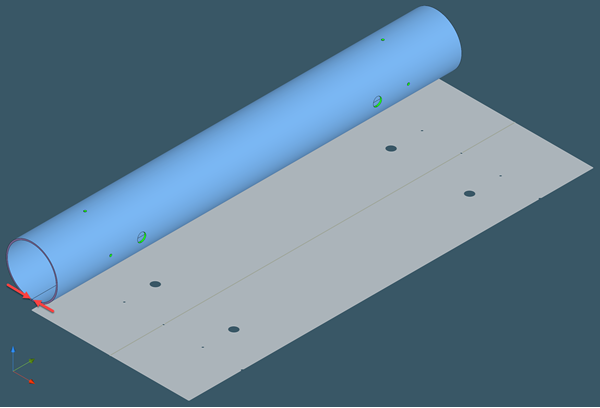This approach is not truly topological because it mainly deals with the analytical geometry of a part. A hardworking reader may notice, however, that this strategy would fail for some fancy types of seam cuts, such as when a cut is not straight (as shown in the images above) but rather zigzag-ish in shape:

In such cases, the spanned angle is perfectly 360 degrees (or even greater, if we compute the sum) because the border cut is not aligned with the curvilinear V axis of a cylindrical surface. Therefore, the geometric check is not enough.

Any better approach?

As we previously noted, topology must be considered when distinguishing between rolled parts and tubes. A real topological approach to detecting seam cuts will allow us to solve the following problems:

• Zigzaggy cuts won't be a problem anymore.

• If a seam cut is made without proximity (i.e., there is no real gap in the part along its cut), then our angular gap heuristic is simply useless. At the same time, the very presence of a seam cut, even without a clearance, is pretty likely an intentional thing that we should not ignore.

In topological language, the requirement of having a seam cut can be formulated, for example, as follows:

Here $n$ is the neighborhood operator returning all faces adjacent to the given set of faces $s$. The implementation of the expression above is fairly trivial:

bool CheckTopoCut(const asiAlgo_Feature&     sheetIds,
                  const asiAlgo_Feature&     innerIds,
                  const asiAlgo_Feature&     thicknessIds,
                  const Handle(asiAlgo_AAG)& aag,
                  ActAPI_PlotterEntry        plotter)
{
  // Get thickness connected components.
  std::vector<asiAlgo_Feature> T;
  //
  aag->PushSubgraph(thicknessIds);
  {
    aag->GetConnectedComponents(T);
  }
  aag->PopSubgraph();
  
  // Get sheet connected components.
  std::vector<asiAlgo_Feature> S;
  //
  aag->PushSubgraph(sheetIds);
  {
    aag->GetConnectedComponents(S);
  }
  aag->PopSubgraph();
  
  // If there EXISTS `t` in `T`...
  for ( const auto& t : T )
  {
    bool any = true;
    
    // ... that for ANY `s` from `S`...
    for ( const auto& s : S )
    {
      // ... `n(s)` ...
      asiAlgo_Feature ns = aag->GetNeighbors(s);
      
      ns.Subtract(innerIds); // exclude inner faces
      
      // ... is a subset of `t`.
      if ( !ns.IsSubset(t) )
      {
        any = false;
        break;
      }
    }
    
    if ( any )
      return true;
  }
  
  return false;
}

With such a heuristic, we can identify a wider range of situations, i.e. a greater diversity of tube-like rolled shapes

As practice proves, the best results are obtained when the geometric check is paired with the topological one. For example, we first verify the spanning angle to ensure that it is close to 360, and then perform a topological check.

More examples

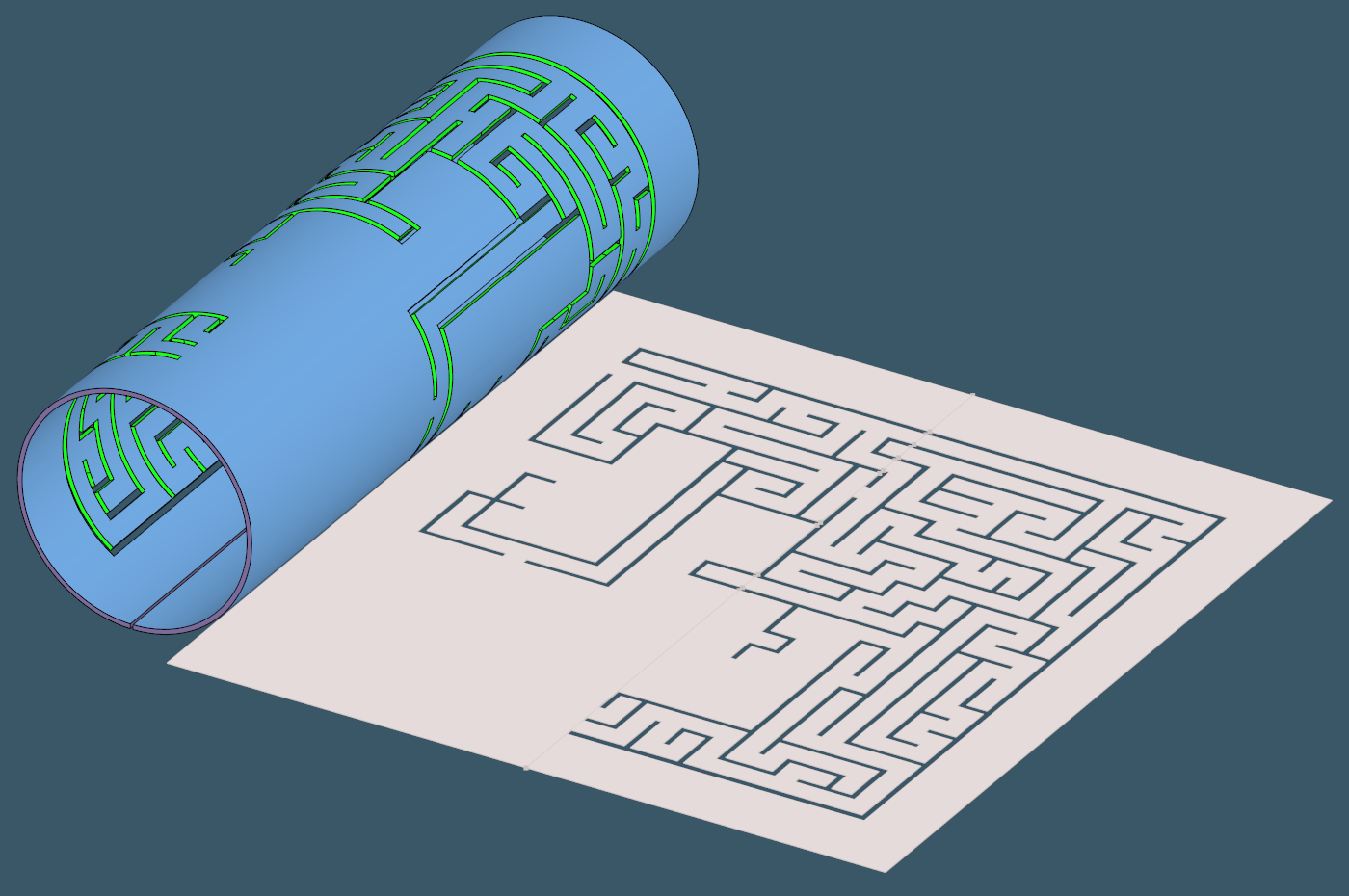
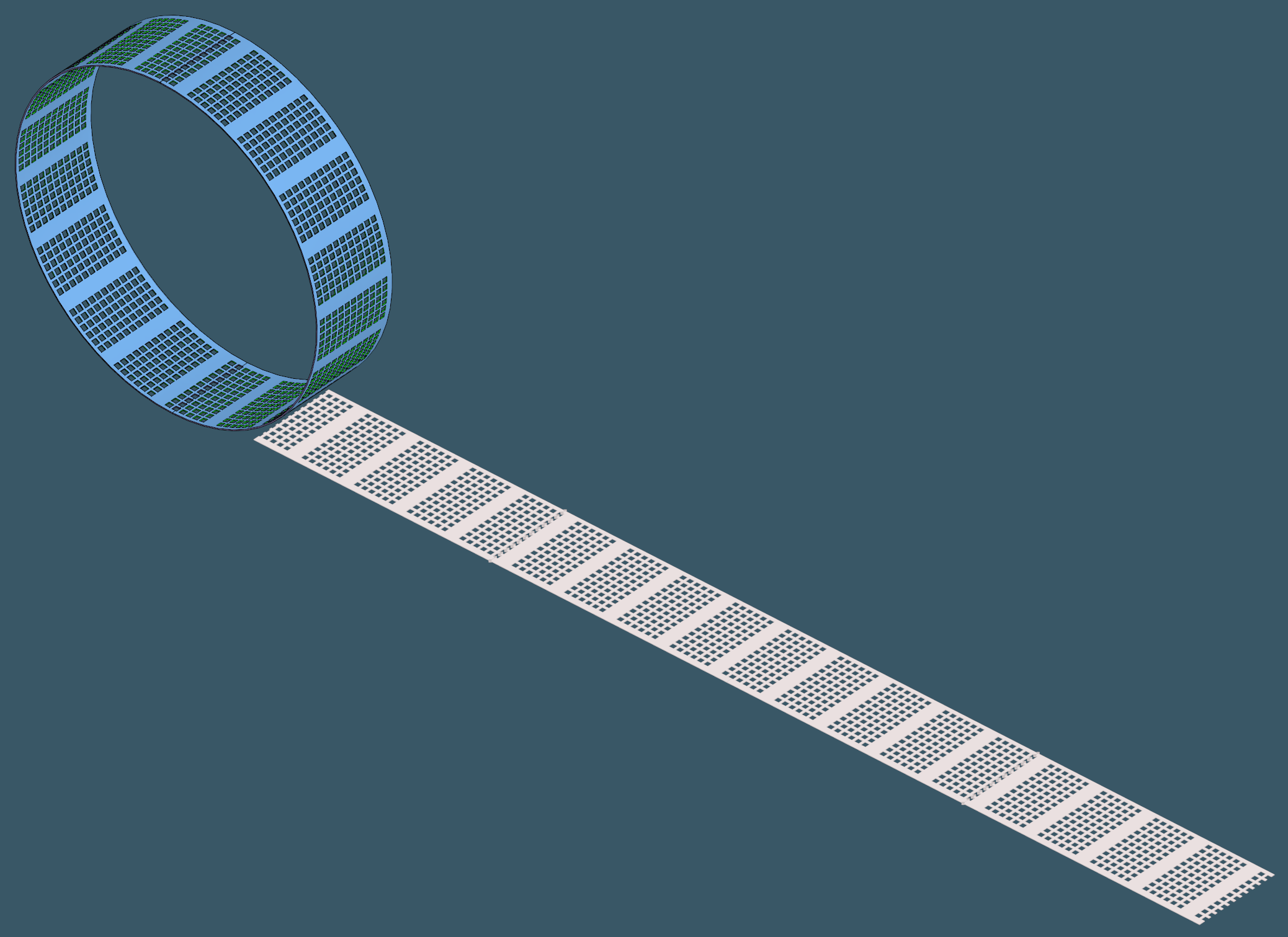
Some examples unlocked thanks to the reworked unfoldability test are presented below.

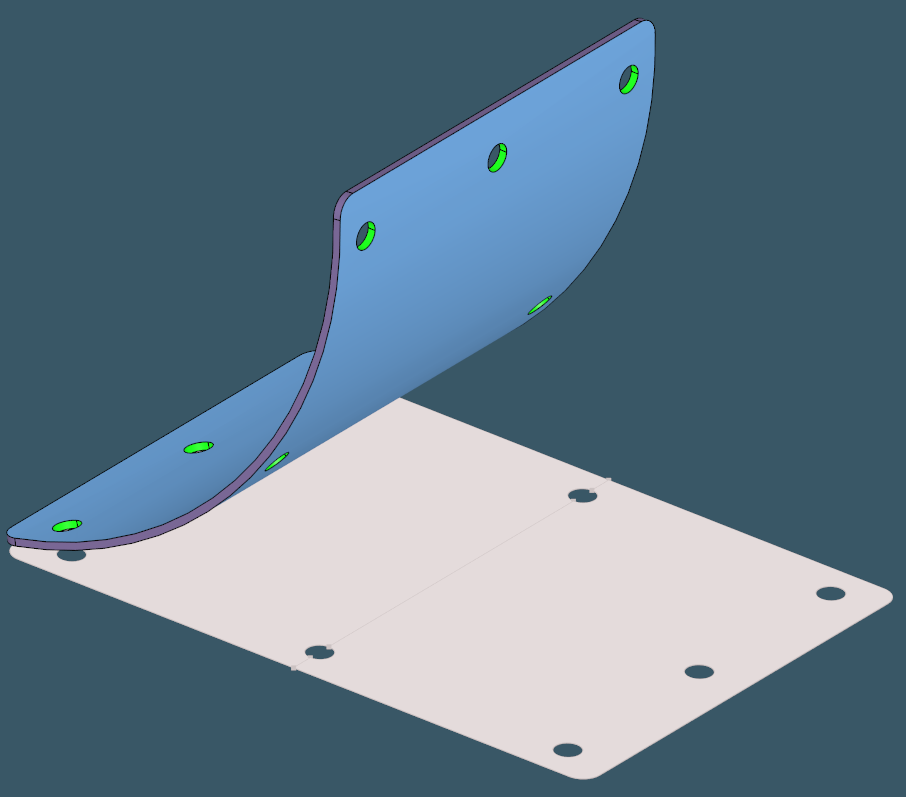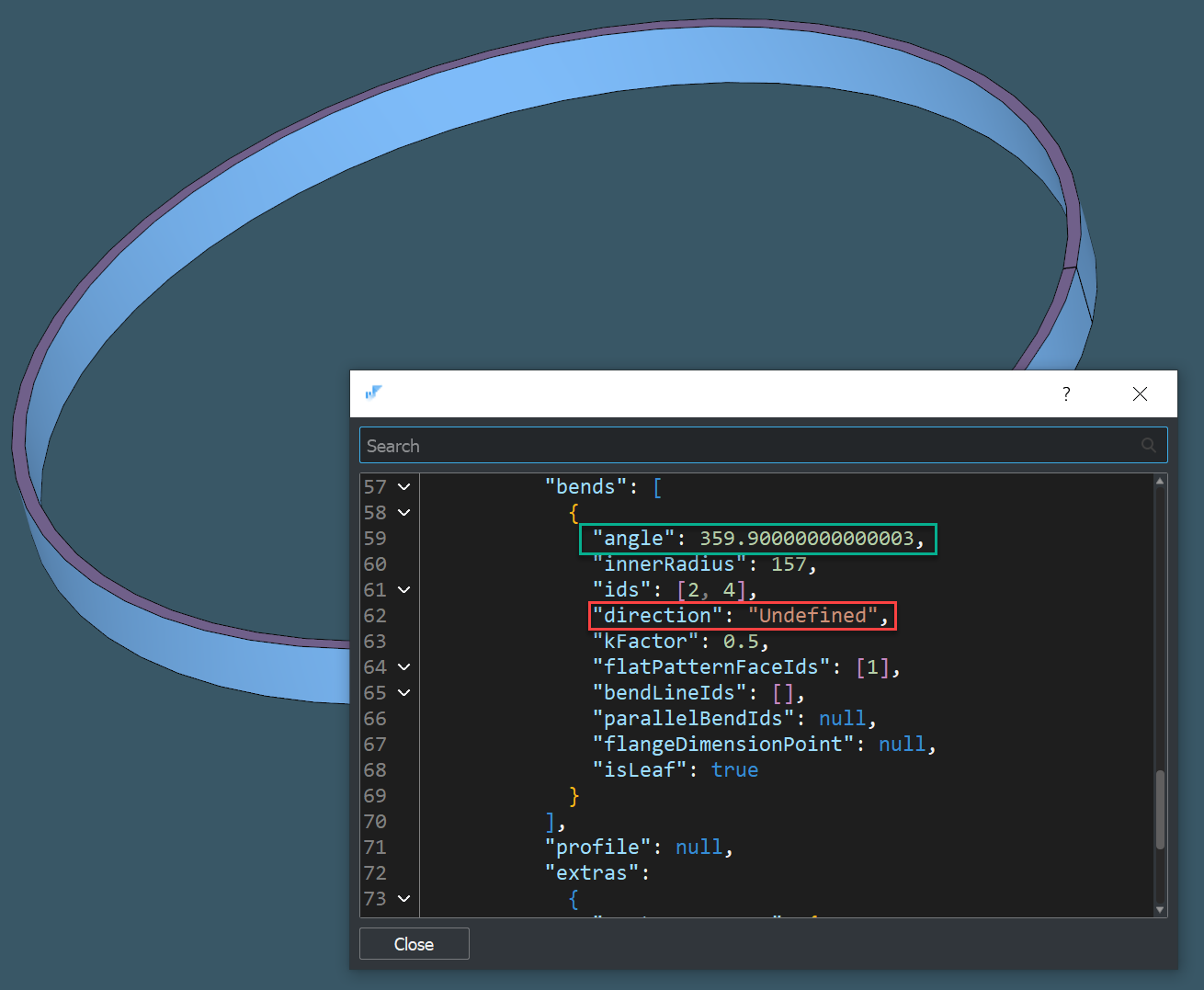Most of these cases look pretty trivial. However, we must not forget that these are primarily extreme cases, and their treatment in the algorithm should not harm the computational architecture of the baseline unfolder. Such enhancements are difficult to implement since mature algorithms typically begin to "resist" any attempt to change their logic. Here can observe the famous Pareto principle. The remaining 20% of the desired output is obtained with 80% of the work.

Want to discuss this? Jump in to our forum.