Булевы операции на B-Rep (введение)
«Природа не терпит голой сингулярности» (Роджер Пенроуз).
Что такое булева операция на B-Rep?
Введение
В мире геометрического моделирования существует некоторое классическое, «стандартное» множество операций, позволяющих конструктору, не привлекая сложной математики, создавать объект почти произвольной формы. Хотя никакого жесткого регламента здесь нет, за многие десятилетия развития трехмерного моделирования в САПР устаканился «джентельменский набор», непременно содержащий такие инструменты, как вытягивание профиля, построение тела вращением контура вокруг оси, скосы, фаски, скругления и прочее. Можно долго и утомительно заниматься классификацией известных нам операций, группировать их по некоторому признаку и сравнивать CAD-системы в их полноте относительно реализуемых функций. Мы не будем заниматься этим нужным и важным делом, а копнем немного глубже. Дело в том, что значительное множество моделирующих функций (подчеркнем, — далеко не все) технически представляют собой не что иное, как специальным образом «заряженные» булевы операции.
Булева операция (БО) в геометрическом моделировании — это «простая» теоретико-множественная операция, объектами которой являются CAD-модели. Булева операция дает инженеру полную свободу в формообразовании, не привлекая каких-либо кинематических соображений (как, например, операция «заметания» вдоль траектории). Платой за гибкость является повышенная сложность подготовки операндов, так как булев алгоритм не является предметно-ориентированным (т.е. формируя конструктивный элемент посредством БО, инженер должен сам позаботиться о соблюдении всевозможных ограничений моделирования). Мы будем говорить только о таких булевых операциях, которые работают на структурах B-Rep (от англ. «Boundary Representation», — граничное представление) в двух режимах:
- Поверхностный
- Твердотельный
Разница между режимами состоит в типе операндов. В первом случае операция выполняется на оболочках, во втором — на телах, ограниченных замкнутыми оболочками. Под оболочкой будем понимать исключительно двумерное многобразие (2-manifold). Базовыми, как известно, являются следующие операции:
- Объединение
- Пересечение
- Вычитание
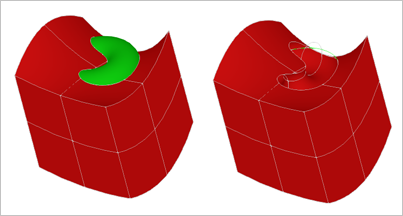
Рис. 1. Результат вычитания тора из криволинейного параллелепипеда (Open CASCADE Technology).
Не уменьшая общности, будем называть объекты (операнды) булевых операций телами, делая оговорки для двумерных оболочек лишь там, где это принципиально важно. Результатом операции объединения двух тел является третье тело, содержащее точки, принадлежащие обоим операндам. Результатом операции вычитания являются все точки первого тела, не содержащиеся во втором. Результатом операции пересечения являются общие точки двух тел. Основной задачей булева алгоритма является конструирование границ финальной модели. Иногда (см., например, [1]) эти алгоритмы называют алгоритмами вычисления и слияния границ (boundary evaluation and merging), что явно подчеркивает их чисто топологическую натуру.

Рис. 2. Тестовая модель Gehause Rohteil, построенная при помощи булевых операций (Open CASCADE Technology).

Рис. 3. Тестовая модель ANC101, построенная при помощи булевых операций (Open CASCADE Technology).
Общая идея булева алгоритма довольно проста и наглядна. Но за этой простотой нас поджидают многие трудности. Дело в том, что «сверхзадачей» булева алгоритма является способность работать и выдавать адекватный результат на произвольных пользовательских данных. В подтверждение общепризнанной сложности дела приведем пару цитат из работ, посвященных булевым операциям:
The more restrictions are imposed on the operations used to create objects one wants to model, the more robust the modeler turns out to be. Creating a robust modeler without imposing restrictions on input and output objects and on the operations the user can perform with these objects is a very difficult task, and still remains a challenge to the developers of geometric modeling systems. [2]
Boolean operation algorithms are among the most complex in solid modeling. They also are among the most difficult to implement reliably, in the presence of round-off errors. [3]
В целом, для булевых алгоритмов следует выделить три ключевых критерия качества:
- Точность. Это первое требование к любой вычислительной схеме. Оно заключается в том, что результат операции должен быть близок к «истинному» результату, причем степень близости (точность) контролируется тем или иным способом. В некоторых случаях, особенно, если операнды соприкасаются, точное вычисление произвести непросто. Случай касания вообще оказывается краеугольным и иногда для того, чтобы подчеркнуть его особый статус, используется слово «сингулярность». Это сильный термин (вспомните хотя бы о космологической сингулярности), но он хорошо отражает суть дела: попав в «сингулярность», мы оказываемся в зоне локально плохой, недоопределенной геометрии, с которой нужно как-то разбираться, исходя из конкретного типа аномалии. Другим источником неточности вычислений являются привычные ошибки округления, связанные с ограниченным представлением вещественных чисел в памяти компьютера. Мы отмечаем здесь этот общеизвестный факт, т.к. существуют некоторые вариации булева алгоритма, пытающиеся бороться именно с этой, второй проблемой.
- Надежность (устойчивость по входным данным) — важнейший критерий качества булева алгоритма. Это понятие, также как и точность, является фундаментальными для вычислительных схем (численных методов). Требование состоит в том, чтобы при незначительном изменении входных данных результат также изменялся незначительно. Скажем, если немного «пошевелить» два операнда так, чтобы они вышли на взаимное касание, то результат булевой операции не должен радикально отличаться от результата в случае без касания. В частности, это означает, что результат должен быть топологически и геометрически корректен.
- Эффективность, понимаемая в смысле расхода памяти и времени процессора. Булевы операции — традиционно тяжеловесные алгоритмы, которые не могут похвастаться быстрым временем отклика, а потому их интенсивное использование в интерактивном режиме на сегодняшний день практически невозможно. Для примера можно взять задачу интерактивного фрезерования (material removal), в процессе решения которой пользователь наблюдает за тем, как исходная модель подвергается булеву вычитанию вдоль некоторой траектории. Если геометрия модели нетривиальна (т.е. состоит не из одних плоских зон), то частые вызовы булева алгоритма (для каждого нового положения фрезы) могут катастрофически сказаться на производительности системы.
Несмотря на бурную историю развития геометрического моделирования, нельзя утверждать, что существует некий единый принцип, согласно которому должен строиться булев алгоритм. В литературе эта функциональность практически всегда описывается без тщательного формализма, предлагая читателю удовлетвориться лишь руководящей идеей алгоритма и, иногда, некоторыми конкретными вычислительными рецептами. После вдумчивого изучения предметной области, приходишь к выводу, что подобный поверхностный стиль скорее всего неизбежен. Дело в том, что стремление охватить булев алгоритм во всей его полноте неизбежно приводит к необходимости описать все патологические случаи, с которыми он способен работать. В рассмотрении этих случаев часто страдает систематичность, поскольку они возникают, как правило, из инженерных задач, представляющих собой неисчерпаемый источник всевозможных патологий. Тот героический автор, который задался бы целью разложить все «по полочкам», скорее всего, был бы вынужден набрать петитом целый справочник аномальных случаев в дополнение к не столь уж громоздкому описанию тела алгоритма. Но мало описать аномалию, надо еще «назначить лечение». И в этом отношении тоже далеко не все благополучно, так как некоторые вычислительные схемы принципиально не способны обработать тот или иной патологический случай. Кроме того, если подобного рода справочник и существует в природе, то едва ли его циркуляция выходит за пределы компании, где ведется разработка алгоритма. Компоненты геометрического моделирования слишком дорогостоящи, чтобы разбрасываться готовыми инструкциями по их реализации.

Твердотельное моделирование в Sketchpad (фото). Справа показаны границы, подлежащие вычислению.
Итак, индустриально надежный булев алгоритм должен иметь достаточно острые зубы и цепкие когти, чтобы выжить в неласковом мире «реальных инженерных моделей», которые нередко далеки от математически совершенного граничного представления (B-Rep). Иногда конкретный вид несовершенства модели оказывается тупиковым для принятой вычислительной схемы, требуя принципиально невозможного улучшения алгоритма. В силу отсутствия какой-либо энциклопедии патологий B-Rep, оценка надежности булевых операций всегда отчасти субъективна. Принимая во внимание бесчисленное множество видов таких аномалий, нужно заключить, что абсолютно надежный булев алгоритм нереализуем. Ниже мы рассмотрим булевы алгоритмы, исходя из общих теоретических оснований, постепенно раскрывая сущность возникающих на нашем пути проблем. В конце обзора мы выведем на сцену общедоступный алгоритм библиотеки Open CASCADE Technology и, тем самым, подготовим почву для более глубокого обсуждения алгоритмов этого класса.
Свойства булева алгоритма
Опишем основные свойства булева алгоритма:
- Булев алгоритм — это чисто топологический алгоритм, т.е. реальный тип геометрии, на котором построены вершины, грани и ребра, не имеет значения. Так или иначе, мы будем иметь в виду параметрически заданную геометрию, как стандарт де-факто в моделировании для САПР.
- Согласно [4] булев алгоритм может только уничтожать границы, но не добавлять новые (речь идет об «отвлеченных» геометрических границах многообразий, а не о топологическом графе B-Rep):
- Булев алгоритм должен быть регуляризованным. В этом аспекте он отличен от формальной теоретико-множественной операции, которая допускает наличие вырождений (в случае точных касаний). В [5] проф. Ари Рекувич приводит чертеж, изображенный на рис. 4.
- $\setminus$ удаляет общие границы, тогда как $\setminus^*$ — нет;
- $\cap$ оставляет общие «висячие» границы, тогда как $\cap^*$ — нет;
- $\cup$ и $\cup^*$ идентичны.
- В результате булевой операции может оказаться, что несколько граней лежат на одной поверхности и поэтому допускают слияние в одну грань (называемую «максимальной» в [4]). Соответствующий механизм упрощения должен присутствовать во всяком булевом алгоритме во избежание нарастающего дробления модели в результате применения серии теоретико-множественных операций. С другой же стороны такое упрощение может быть иногда излишним (это зависит от намерений проектировщика), поэтому должно быть доступно как опция.
- Согласно [1], необходимость рассмотрения множества специальных случаев для взаимного расположения операндов является спецификой булева алгоритма, не зависящей от его конкретной реализации. Мы уже обсудили этот вопрос во введении, отметив, что невозможно создать абсолютно надежный булев алгоритм. Нам важно теперь подчеркнуть эту особенность как характерное свойство алгоритма. После машинной реализации БО вносить принципиальные изменения в вычислительную схему (при возникновении аномалий на входе) будет дорого, а иногда и попросту невозможно. Поэтому изначально жизненно важно продумать структуру алгоритма так, чтобы она была по возможности максимально гибкой.
- Множество 2-многообразий («два-многообразий») незамкнуто относительно регуляризованных булевых операций. Под 2-многообразием понимается фигура, всюду локально подобная (гомеоморфная) диску окружности. Если для любой точки нашей поверхности мы можем вообразить, что ее окрестность непрерывно переходит в круг, то такая поверхность является 2-многообразием. Многообразные поверхности — это хорошо, поскольку в них нет внутренних перегородок (усложняющих работу с моделью) и они реализуемы «в железе» (нет бесконечно истонченных сопряжений, толщиной «в один атом»). Проще говоря, реализовать геометрическое ядро, работающее на немногообразной геометрии — задача более сложная, чем в случае, когда мы ограничиваемся 2-многообразиями. Возвращаясь же к булевым операциям, нетрудно видеть, что на многообразных операндах они, вообще говоря, выдают немногообразный результат (рис. 6).
$\delta ( A \otimes B ) \subseteq ( \delta A \cup \delta B )$
Здесь символ $\delta$ обозначает границу многообразия ($A$ и $B$), а знак $\otimes$ — теоретико-множественную операцию (объединение, пересечение или вычитание). Это основное соотношение («boundary inclusion relationship» — отношение включения границ) является в то же время алгоритмичным, т.к. указывает способ получения результата. Сначала мы объединяем все границы в одно множество, а затем реализуем конкретную операцию $\otimes$ путем уничтожения лишних границ в соответствии с типом операции.
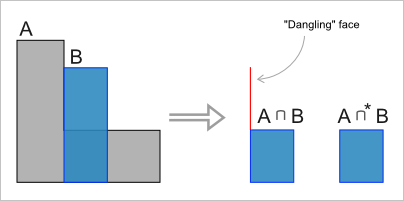
Рис. 4. Нерегулярный и регулярный объекты в результате операции пересечения (вид сбоку).
Из рис. 4 мы видим, что в результате операции пересечения образовалась «висячая» («dangling») грань, наличие которой с формальной точки зрения неизбежно, т.к. она принадлежит обоим операндам и, следовательно, войдет в результат теоретико-множественного действия. Этот эффект наглядно свидетельствует о том, что размерность объекта не является инвариантом теоретико-множественных операций (при операции над трехмерными объектами образовалась двумерная область). С инженерной точки зрения полученная грань бессмысленна, т.к. она является бесконечно тонкой. Для преодоления этой трудности вводится понятие регуляризованной булевой операции $\cup^*$, $\cap^*$ и $\setminus^*$. Идея состоит в том, чтобы в результате операции над регулярными объектами (которыми являются тела в геометрическом моделировании) снова получался регулярный объект. Напомним, что область пространства называется регулярной, если она в точности совпадает с топологическим замыканием своей внутренности. Таким образом, регуляризованные булевы операции над телами всегда возвращают топологически корректное (возможно пустое) тело без «висячих» граней, ребер и вершин.
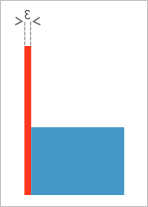
Рис. 5. Тонкий «паразитный» слой.
Регуляризованные теоретико-множественные операции являются общепринятыми в твердотельном моделировании. В сравнении с классическими теоретико-множественными операциями отметим следующее:
Попросту говоря, регуляризованная операция деликатно обходится с границами объекта, не допуская деградации размерности и нарушения компактности (замкнутости и ограниченности) результата.
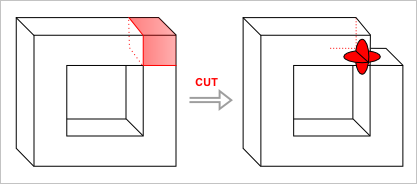
Рис. 6. Немногообразный стык.
Понятно, что запретить булевой операции выдавать результат, проиллюстрированный на рис. 6, мы не можем (иначе она перестает адекватно работать). Но это и не нужно. Если мы хотим избавиться от немногообразной геометрии, достаточно разрушить информацию о принадлежности ребра на стыке сразу четырем граням, введя два геометрически совпадающих ребра, принадлежащих не более, чем двум граням каждое (рис. 7). Альтернативным решением будет допущение немногообразной топологии, но в этом случае мы должны быть уверены, что все прочие моделирующие алгоритмы способны обработать такую ситуацию корректно. Так, например, способен ли алгоритм построения скруглений расщепить единственное немногообразное ребро на два в случае, если это ребро было выбрано пользователем для построения поверхности сопряжения? Проблемы подобного рода могут настолько усложнить дело, что дешевле становится запретить немногообразную геометрию, чем пытаться с ней корректно работать на общих основаниях.
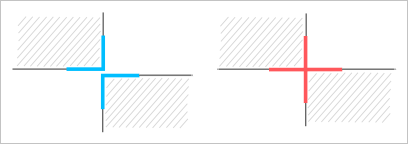
Рис. 7. Многообразный и немногообразный стыки (вид сбоку). Зазор, изображенный слева, на самом деле не существует.
Обзор литературы
Давайте разберемся, какова история булева алгоритма и что заинтересованный инженер-программист от САПР может почитать по данному вопросу. Среди всех материалов, особого внимания, на наш взгляд, заслуживают следующие:
- A.G. Requicha (Ари Рекувич) [4] и [5]. Опубликованная в 1984 году брошюра «Boolean Operations in Solid Modeling: Boundary Evaluation and Merging Algorithms» [5], может считаться одной из первых теоретических работ, посвященных регуляризованным теоретико-множественным операциям в твердотельном CSG и B-Rep моделировании. Это работа общего плана, дающая математическую модель задачи и некоторые рецепты для реализации численного алгоритма. С практической точки зрения работа подкреплена реализацией алгоритма в системе PADL, созданной в университете Рочестера. Также Рекувич читал специальный курс, посвященный геометрическому моделированию, в котором булевым операциям и смежным алгоритмам была посвящена отдельная глава. Следует, однако, заметить, что лекционные материалы [4] больше похожи на черновики, и не отличаются ни полнотой, ни стройностью изложения.
- C.M. Hoffmann (Хоффманн) [1]. Этот труд Хоффманна упоминается в популярной статье Н. Снытникова [6] как дающий «стандартный» подход для реализации булева алгоритма. Он был издан в 1989 году, но не теряет своей ценности и по сей день. Изложение опирается на полигональное представление геометрии, хотя общность постановки задачи от этого не страдает (что явно подчеркивается автором). Математическая модель в работе Хоффманна не играет первую скрипку. Руководствуясь триадой А.А. Самарского «Модель-Алгоритм-Программа», можно заметить, что собственно математическому моделированию задачи внимания уделяется мало. По существу, здесь описывается только алгоритм.
- В работе [2] M.C. Arruda (Арруда) занимается развитием подхода проф. Мантила (Martti Mantyla, фин.) [7] и указывает на успешное применение разработанного алгоритма в конкретной бразильской CAD-системе. Однако изложение фокусируется преимущественно на классификации и удалении границ (boundary merging), каковая является вторым шагом общей схемы алгоритма. Вопросы создания модели слияния (boundary evaluation) не рассматриваются, и в целом повествование лишено деталей, особенно в части рассмотрения патологических случаев.
- В работе [8] J. Keyser (Кейзер) рассматривает задачу точного вычисления границ для криволинейных тел (curved solids). Результатом его работы стала некая система ESOLID (надо полагать, первая буква означает «Exact»), применяемая для вывода граничного представления моделей в форме CSG, причем базовая геометрия модели представлена полиномами невысоких степеней (2-4). Если встречаются объекты высших порядков, то должна быть проведена операция декомпозиции на несколько более простых объектов. Работа Кейзера оригинальна в том плане, что предлагаемый булев алгоритм избавлен от ошибок округления, благодаря внедрению в алгоритм вычислений с произвольной точностью (exact arithmetic). Мы, однако, не станем концентрироваться на данной работе, поскольку для ее практического внедрения требуются слишком жесткие ограничения на вычислительную систему в целом. Именно, мы должны ограничиться объектами в формате CSG, выпуская из внимания любые модели, где допускается небрежность стыков (толерантная геометрия). Так, защита от каких угодно ошибок округления не сильно нам поможет в случае, если операнды БО читаются из файла STEP, записанного при помощи CAD-системы, где с ошибками округления (и более существенными источниками неточностей) никто и не думал бороться. Таким образом можно ставить крест на обмене данными. Другая проблема, очевидно, проистекает из крайней ресурсоемкости точных вычислений, ухудшающих быстродействие системы на порядки (что и отмечает Кейзер в своей работе).
- S. Krishnan et al (Кришнан) [9] и [10]. Эти работы более современны по сравнению с «классикой». В частности, Кришнан обсуждает вопросы параллельных вычислений границ B-Rep объектов, указывая, что разработанный метод отличается высокой точностью и скоростью. Здесь мы имеем дело с достаточно общим алгоритмом, требующим представления исходных моделей в виде лоскутов Безье. Последнее обстоятельство не является слишком серьезным препятствием, так как даже сложные NURBS-поверхности сводимы к этой форме (см., например, [11]). Следует обратить самое пристальное внимание на оригинальный способ поиска пересечения двух поверхностей, используемый в работах Кришнана. Работа [9] не должна остаться без внимания также еще и потому, что в ней приводятся конкретные вычислительные рецепты для неполигональных моделей. В частности, Кришнан перечисляет некоторые патологические случаи, множество которых, вообще говоря, отлично от того, что мы имеем для чисто планарной геометрии. Типы вырождений, перечисляемые Кришнаном, общие вычислительные принципы и даже архитектурные аспекты реализации булева алгоритма — все это может и должно быть учтено исследователем. Система, описываемая Кришнаном, назвается BOOLE и уже по названию мы можем заподозрить некоторое сходство с системой ESOLID Кейзера, описанной выше. В самом деле, оба автора работали рука об руку, соревнуясь, какой алгоритм лучше: точный и медленный, либо неточный и быстрый? Едва ли уместно давать готовый ответ на этот вопрос, не поставив вычислительный эксперимент. Однако стоит сказать, что алгоритмы вычислительной геометрии по преимуществу реализуются в среде неточной арифметики.
- Н.Н. Голованов [12] описывает алгоритм, реализованный в геометрическом ядре C3D. Здесь дается общая схема вычислений без конкретизации деталей, в которых, как известно, прячется дьявол. Вычислительная схема дана пунктирно, так как в формате небольшой монографии вдаваться в подробности булева алгоритма было бы неразумно. С этим описанием, равно как и со всей монографией Н.Н. Голованова, следует обязательно ознакомиться и даже иметь у себя на столе.
Ниже мы сфокусируемся главным образом на работe Рекувича [5]. Хоффманну были известны работы Рекувича — некоторые упоминаются в монографии [1]. По нашему мнению, эта работа Хоффманна смещает акцент с чисто математического взгляда на проблему в сторону ее машинной реализации. Не умаляя достоинств работы Хоффманна, мы все-таки согласимся с точкой зрения Рекувича о том, что геометрические алгоритмы проще всего понять, если они описываются, исходя из общих соображений, используя математический язык (благо, здесь он не требует глубокого владения топологическим аппаратом). Наличие математической модели избавляет нас от необходимости удерживать ускользающие сквозь пальцы чисто словесные формулировки и их комбинации. Такие формулировки обычно плохо структурированы, нелаконичны и невзвешенны в том смысле, что помимо чисто теоретических резонов, в них вживляются конкретные вычислительные рецепты. Эти, последние, хотя и важны на практике, должны опираться на строго вычерченную теоретическую концепцию, выявляя ее детали в прикладных приложениях. Работа Хоффманна [1] не дает математической формулировки для регуляризованных теоретико-множественных операций. Однако в ней могут быть найдены ценные советы общего плана, такие как «avoid asking the same geometric question more than once», что позволяет не просто повысить надежность наших алгоритмов, но и выбрать для них правильную руководящую идею.
Reliable geometric algorithms cannot be designed in the absence of a clear mathematical statement of the problem to be solved. [13]
В своей брошюре [5] Рекувич опирается на классификацию «пробы» (probe) $X$ относительно модели $S = A \otimes B$, где $\otimes$ обозначает булеву операцию. Суть дела сводится к выбору множества проб и их классификации указанным образом. Множество проб в случае B-Rep должно получаться из исходных границ моделей $A$ и $B$. Классификация пробы синтезируется из ее классификации относительно операндов $A$ и $B$, которая может осуществляться только при наличии дополнительной информации о взаимном расположении операндов. Эта информация вводится в рассмотрение через понятие окрестности (neighborhood) граничных точек. Работа Рекувича развивает работу Тилаува (Tilove) [13] от 1980 г. Обе работы используют по существу один и тот же язык («рочестерский жаргон»). Более того, описываемой общей схемы придерживается и Арруда в [2], чего, однако, нельзя сказать о Хоффманне в [1], что еще больше отрывает его работу от «рочестерской школы». С другой стороны Хоффманн так или иначе использует те же подходы, что и Рекувич. Читая работы Хоффманна и Рекувича, нельзя также не заметить, что многие специальные замечания Хоффманна проистекают из соображений повышения надежности алгоритма, тогда как Рекувич делает акцент на производительности. В целом, обе работы дополняют друг друга. В порядке их изучения имеет смысл придерживаться естественной хронологии, т.е. начать с работы Рекувича [5], после чего обратиться к монографии Хоффманна [1] за дополнительными разъяснениями некоторых технических тонкостей. Работа Кришнана [9] в этой схеме может играть дополняющую роль, так как в ней, помимо ценных теоретических указаний, содержатся сведения о внедрении параллелизма в основные этапы булева алгоритма. Мы не могли бы с легкостью использовать [9] с самого начала, так как это потребовало бы предварительной разработки основополагающих геометрических алгоритмов и подходов, таких как пересечение поверхностей и способ представления твердых тел. Едва ли такая серьезная работа должна быть выполнена в случае, если мы хотим оставаться в рамках некоторого конкретного геометрического ядра с его наличествующими геометрическими функциями, например, ядра Open CASCADE Technology.
Ниже мы рассмотрим структуру алгоритма Рекувича для твердотельных булевых операций над B-Rep.
«Пугливый» алгоритм Рекувича

Рис. 8. Ари Рекувич — один из пионеров геометрического моделирования. Его отличает строгий подход к математической формализации проблемы.
В работах [4] и [5] представлена упрощенная версия алгоритма, реализованного в системе PADL-2 (Part & Assembly Description Language). Эта система разрабатывалась в рамках проекта по автоматизации производства (PAP = Production Automation Project) в университете Рочестера, начиная с 1972-го и по 1987 год. PAP был основан профессором Гербертом Велкером (Herbert Voelcker) для нужд программирования станков с ЧПУ (см. главу 2 в [14]). В 1973 году к Велкеру присоединился Ари Рекувич, после чего группа исследователей переключилась на задачи твердотельного моделирования. В результате была создана система PADL-1, совмещающая в себе технологии CSG и B-Rep. Проект PADL-2 был инициирован в начале 1979 года, а первая версия вышла в 1981 году. Обе системы были написаны на языке FORTRAN. Они использовались не только для обучения студентов геометрическому моделированию, но также для подготовки персонала САПР промышленных предприятий (см. [15]).
В [5] Рекувич указывает, что предлагаемый булев алгоритм был создан в середине 1970-х, но никогда прежде не излагался. На момент написания меморандума [5] булевы операции твердотельного моделирования, хотя и были реализованы в некоторых CAD-системах, но соответствующих им научных или технических публикаций в широком доступе не существовало. Пятнадцатилетний рочестерский период дал многое для развития САПР. Формировалось теоретическое ядро твердотельного моделирования, а вместе с ним и язык, который профессор Рекувич именует «рочестерским жаргоном». Многое из этого жаргона вошло в современную терминологию, которой мы и будем пользоваться ниже.
Requicha and Voelcker are true solid modeling pioneers, who shaped the field. Their research and education efforts will be felt for years to come. [16]
Классификация граней
В [4] предлагается следующая концептуальная схема алгоритма для регуляризованной булевой операции $S = A \otimes B$:
Generate_Tentative_Faces(A, B);
for each face F do
{
FwrtS = Classify_wrt_Solid(F, S)
Add_to_BRep(FonS);
}
Здесь явно выделены следующие этапы:
- Поиск «эффективных» граней (Generate_Tentative_Faces);
- Классификация эффективной грани относительно результирующего тела $S$ (FwrtS означает «Face with respect to Solid»);
- Сборка границ (boundary merging) итоговой модели (Add_to_BRep). Учитываются только те грани (точнее их части), которые лежат на границе $S$.
Предложенная схема, хотя и была оформлена Рекувичем посредством псевдокода, не является технологичной. По существу, она дает лишь первый шаг в серии аналитической декомпозиции общей постановки задачи на более конкретные этапы. Мы могли бы предложить читателю, не откладывая, итоговую версию алгоритма, но такой путь был бы слишком «варварским» и, двигаясь по нему, мы не увидели бы ни изначального хода рассуждений Рекувича, ни многих тонкостей, представляющих особый интерес.
Классификация ребер
Общая схема, представленная выше, предполагает классификацию граней относительно результирующего тела (FwrtS). Для этого нам понадобится соответствующая утилита — «классификатор граней». Однако, учитывая, что мы работаем с представлением B-Rep, классификацию граней можно заменить классификацией ребер (понизив тем самым размерность задачи). Заметим здесь (и это важно), что какой бы классификацией мы не пользовались, существо дела остается неизменным: его можно выразить парадигмой generate-and-classify (или, что то же самое, generate-and-test). В первом случае мы говорим о схеме generate-and-classify на гранях, во втором — на ребрах. Таким образом ставится задача о конструировании реберного представления тела $S$, для которой можно по аналогии предложить следующую схему:
Generate_Tentative_Edges(A, B);
for each edge E do
{
EwrtS = Classify_wrt_Solid(E, S)
Add_to_BRep(EonS);
}
В этом псевдокоде ничего существенно не изменилось. Нетрудно видеть, что в результате булевой операции возможно появление новых граничных кривых — кривых пересечения граней. Это обстоятельство можно отнести на счет процедуры Generate_Tentative_Edges, которая теперь не только разыскивает ребра-кандидаты среди границ операндов $A$ и $B$, но и берет на себя функцию пересечения граней для получения новых ребер. В этом состоит отличие реберной схемы от той, что предложена выше: там новые ребра должны были появиться на этапе классификации. Итак, мы имеем здесь следующие этапы:
- Generate_Tentative_Edges — создание множества пробных (probe, tentative) ребер (рис. 9);
- Классификация ребра относительно тела. Заметим здесь, что классификаторы ребер, принадлежащих $A$, известны: $EonA$. Остается провести классификацию относительно $B$, после чего, воспользовавшись правилами Тилаува (изложенными в [5] и [13]), получить классификацию ребра относительно $S$, т.е. вывести классификатор $EwrtS \in \{EinS, EonS, EoutS\}$. Аналогично мы поступаем с ребрами $B$. Что же касается ребер пересечения, то их, вообще говоря, классифицировать не надо, т.к. они уже в силу самого способа их построения должны войти в результат в отношении $EonS$. Ниже мы, однако, сделаем вслед за Рекувичем одно замечание по этому поводу.
- Добавление ребра в результирующую структуру B-Rep. На этом этапе необходимо связать одиночные ребра друг с другом, формируя итоговый топологический граф.
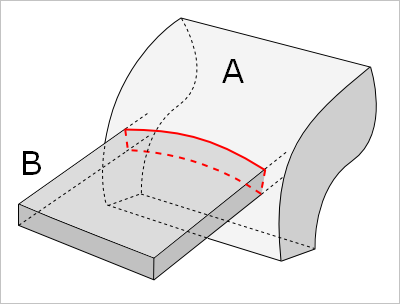
Рис. 9. Новые ребра образуются в результате пересечения граней операндов.
Рекувич выделяет два типа ребер: self-edges (собственные ребра), как подмножества ребер исходных операндов $A$ и $B$, и cross-edges (ребра пересечения), получаемые в результате пересечения граней. В совокупности два этих набора определяют все множество кандидатов для последующей классификации. Отметим также, что эти два термина (self-edges и cross-edges) хорошо прижились в литературе по булевым операциям для B-Rep.
Теперь мы готовы дать простой, но исчерпывающий псевдокод для булева алгоритма.
Схема алгоритма Рекувича
Итак, все ребра операндов $A$ и $B$ можно взять в качестве собственных ребер для классификации. Ребра пересечения нужно получить путем пересечения граней, после чего эти ребра автоматически отправляются в результирующее тело $S$.
//------------------------------------
// Full procedure for self-edges of A
//------------------------------------
for each face F of A do
{
for each self-edge E of F do
{
EwrtA = (E, Neighborhood(E, A)); // Read from the B-Rep of A
EwrtB = Classify_Edge_wrt_Solid(E, B); // Classify against B
EwrtS = Combine_Classifications(EwrtA, EwrtB, OPERATION);
Add_to_BRep(EonS);
}
}
//------------------------------------
// Full procedure for self-edges of B
//------------------------------------
for each face F of B do
{
for each self-edge E of F do
{
EwrtB = (E, Neighborhood(E, B)); // Read from the B-Rep of B
EwrtA = Classify_Edge_wrt_Solid(E, A); // Classify against A
EwrtS = Combine_Classifications(EwrtA, EwrtB, OPERATION);
Add_to_BRep(EonS);
}
}
//------------------------------------
// Full procedure for cross-edges
//------------------------------------
for each face F of A do
{
for each face G of B do
{
if not Surf(F) == Surf(G) then
{
E = IntersectFacesWithAllContours(F, G);
Add_to_BRep(E);
}
}
}
Мы видим здесь, что классификация ребер сопровождается некоторой дополнительной информацией об их окрестности, что отмечено в коде посредством функции Neighborhood. Ниже мы обсуждаем, для чего эта информация была введена в алгоритм. Забегая вперед, отметим, что без информации об окрестности комбинация принадлежностей $[XinA, XonA, XoutA]$ и $[XinB, XonB, XoutB]$ в $[XinS, XonS, XoutS]$ была бы невозможна.
Здесь же мы остановимся на другой важной тонкости. Приведенный псевдокод избавляет нас от необходимости заниматься классификацией ребер пересечения. Это и понятно, ведь конструктивно такие ребра не могут иметь иной классификации, кроме как $XonS$. Рекувич делает важное замечание по этому поводу. Дело в том, что конструирование ребер пересечения — задача далеко не тривиальная. Помимо необходимости поиска линии пересечения поверхностей (что само по себе доставляет немало трудностей), мы должны учесть контуры граней, которые, вообще говоря, отсекают не только внешние области поверхностей, но и моделируют, например, отверстия в них. Эта сложность целиком спрятана в функции IntersectFacesWithAllContours, и мы могли бы удовлетвориться таким описанием, не вдаваясь в детали ее реализации. Однако следует заметить, что указанная сложность может быть преодолена без необходимости введения принципиально новых для нас алгоритмов. Схема, предлагаемая Рекувичем, может быть описана следующим образом:
//------------------------------------
// Full procedure for cross-edges
//------------------------------------
for each face F of A do
{
for each face G of B do
{
if not Surf(F) == Surf(G) then
{
C = IntersectSurfaces(Surf(F), Surf(G));
СwrtF = Classify_Edge_wrt_Face(С, F);
СwrtG = Classify_Edge_wrt_Face(С, G);
E = RegularizedCommon(СinF, СinG)
Add_to_BRep(E);
}
}
}
Таким образом, мы переходим от пересечения граней (рис. 10) к пересечению поверхностей (рис. 11) и сводим обработку контуров граней к двумерной классификации ребра относительно $F$ и $G$ с последующей одномерной булевой операцией взятия общего (рис. 12).
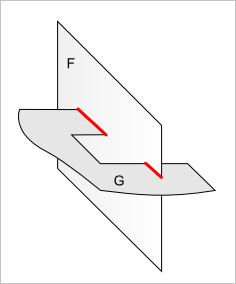
Рис. 10. Пересекаются две грани с внешними контурами сложной формы.
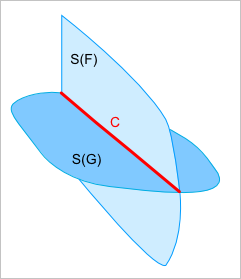
Рис. 11. Вместо пересечения граней ищем пересечение поверхностей.
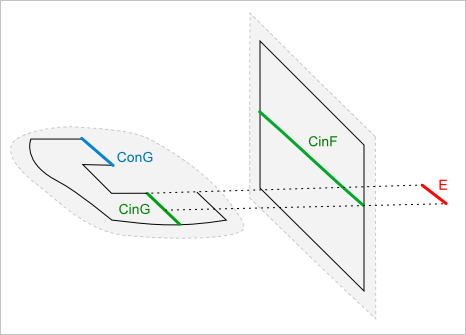
Рис. 12. Для получения итогового ребра используем одномерную булеву операцию. Заметим, что сегмент $ConG$ выводится из рассмотрения.
Из рис. 12 видно, что сегмент $ConG$, представляющий собственное ребро грани $G$, не может войти в результат, так как мы условились использовать функцию RegularizedCommon на множествах $CinF$ и $CinG$. Сделаем по этому поводу два дополнительных замечания:
- Во-первых, не следует тревожиться о том, что сегмент $ConG$ окажется потерян. В действительности он будет обработан другой частью алгоритма как собственное ребро грани $G$.
- Во-вторых, здесь мы имеем дело с сингулярностью, а именно со случаем частичного касания грани $G$ и грани $F$. Касание, в силу каких-либо причин, связанных с погрешностями ли округления или с точностью самого этого касания, может обернуться тем, что сегмент $ConG$ будет опознан как $CinG$. С одной стороны, никакой беды в этом нет, ведь классификатор $CinG$ по существу означает, что данный сегмент не может являться собственным ребром $G$. С другой стороны, — и это важно заметить, — данный сегмент разыскивается процедурой, которая не имеет никакого отношения к обработке собственных ребер, а значит, чисто теоретически, может оказаться, что собственное ребро получает классификатор $CinG$ и будет обработано дважды! В известном смысле здесь нарушается принцип Хоффманна: «avoid asking the same geometrical question twice». Однако вместо того, чтобы пытаться как-то предотвратить подобного рода трудность, возникающую из-за того, что ребра пересечений могут найтись среди множества собственных ребер, имеет смысл обратить пристальное внимание на функцию Add_to_BRep. А именно, следует потребовать от данной функции тщательной выбраковки тех ребер, которые не могут принять участия в итоговой структуре B-Rep в силу того, что их место уже невакантно.
Мы коснулись здесь очень важного вопроса обработки сингулярностей. Ниже мы увидим, что, всякий раз, встретив сингулярность, следует задаться вопросом: нельзя ли ее обойти? Попытка обработать сингулярность всегда менее надежна, чем ловкий способ «сбежать» от нее. Мы еще вернемся детально к этому вопросу в будущем, но пока отметим, что алгоритм Рекувича может стать существенно ненадежным именно из-за «плохой» реализации функции Add_to_BRep. Так, из самой структуры алгоритма видно, что предлагаемая вычислительная схема инкрементальна, то есть последовательна. Шаг за шагом классифицируя новое ребро, мы добавляем его в результат, не оказывая явным образом влияния на те ребра, что были помещены туда на предыдущих этапах. Это — рискованный подход, и в будущих заметках мы обсудим, почему.
Окрестность и граничный переход (neighborhood and transition)
Термин «transition» используется в работе Рекувича для обозначения эволюции признака ${in, out, on}$ вдоль кривой или луча, пересекающего грань тела. Всюду ниже мы используем словосочетание «граничный переход» в качестве его русскоязычного эквивалента. Граничный переход — это эволюция признака принадлежности. Он назначается в каждой точке пересечения кривой с телом, характеризуя процесс качественного изменения окрестности точки вдоль этой кривой (рис. 13). Понятно, что говорить о граничных переходах нельзя безотносительно направления, выбранного вдоль кривой.
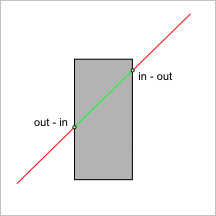
Рис. 13. Точки граничного перехода позволяют выделить внутреннюю часть ребра.
Итак, мы определили граничный переход, как изменение качества окрестности точки, но ни слова не сказали о природе этой окрестности. Необходимость привлечения окрестности обсуждается Рекувичем в работе [5] в связи с недостаточностью рассмотрения только лишь классификации точки относительно множества. Чтобы убедиться в такой недостаточности предлагается модельный пример (рис. 14).
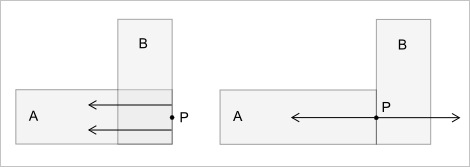
Рис. 14. Точка $P$ имеет классификаторы $PonA$ и $PonB$, но мы не можем сказать, как тела $A$ и $B$ расположены относительно этой точки, пока не изучим ее окрестность.
Отношения $in$ и $out$ однозначно позиционируют точку относительно тела в том смысле, что сколь угодно малая ее окрестность либо сплошь состоит из других точек тела, либо не содержит их вовсе. Сложнее дело обстоит с отношением $on$, так как здесь возможны несколько вариантов, и какой реализуется на самом деле мы знать не можем. Чтобы избежать этой неоднозначности классификатор $on$ должен быть обогащен информацией о типе окрестности, которая наличествует в данной точке. Только теперь, исходя из соотношения окрестностей, т.е. привлекая свойства геометрии «в малом», мы можем вывести конкретный тип граничного перехода (рис. 15).
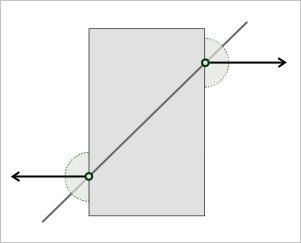
Рис. 15. Граничный переход вычисляется при помощи информации об окрестности в данной точке.
Рекувич выделяет два способа задания окрестности: явный (геометрический) и неявный (топологический). В случае явного задания мы имеем дело с конкретным геометрическим описанием формы окрестности. В случае неявного задания окрестность представляется в виде указателей на смежные граничные элементы. Рекувич указывает, что неявный способ сопряжен с трудностями на этапе комбинирования окрестностей, поэтому он отдает предпочтение явному способу. В будущих заметках мы обратимся к некоторым типам окрестностей, использование которых полезно на практике.
Классификация Точка-Тело
В теории множеств вводится понятие индикаторной функции или, проще говоря, индикатора:
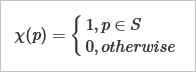
Функция $\chi$ указывает для всякого элемента $p$, принадлежит ли он целевому множеству $S$. В геометрическом моделировании мы хотели бы иметь для каждого тела $S$ аналог этой функции. Однако, коль скоро речь идет о граничном представлении тел, то разумно потребовать от индикаторной функции немного большего, а именно, различать те случаи, когда пробный элемент $p$ лежит на границе. Эта «улучшенная» функция в англоязычной литературе имеет название point membership classification (PMC) или, по-русски, классификация точки на принадлежность. Формализуем:
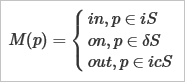
Здесь через $iS$ обозначена внутренность тела, $\delta S$ — его граница, а $icS$ — это внутренность дополнения к $S$.
В зависимости от того, какой способ представления выбран для тела $S$, используется тот или иной численный метод для нахождения значений $M(p)$. Нас интересует граничное представление (B-Rep), для которого может быть адаптирован очень простой алгоритм «испускания лучей» или рейкастинг (ray casting). Из пробной точки $p$ в произвольном направлении строится луч и подсчитывается количество пересечений луча с гранями тела $S$ (или ребрами замкнутого полигона в двумерном случае). Если это число оказывается нечетным, то точка $p$ лежит внутри, в противном случае — снаружи (рис. 16).
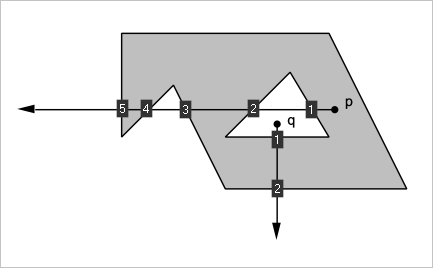
Рис. 16. Метод испускания лучей, хорошо работающий для идеальной геометрии.
Следует заметить, что на практике эта простота обманчива. Во-первых, в предложенном алгоритме нет ни слова о принадлежности точки границе (классификатор on). Во-вторых, испускаемый луч может случайно пройти через одну из вершин или выйти на касание с одной из границ. Как считать пересечения в этих неприятных ситуациях? Рекувич приводит пример одного «совсем испорченного» полигона, где указанные проблемы предстают во всей красе (рис. 17).
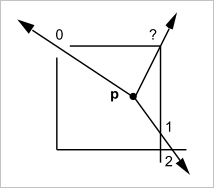
Рис. 17. А реальный мир, как обычно, сложнее.
На рис. 17 мы видим «неудачно» испущенные лучи, попадающие в окрестности вершин, где имеется стык между ребрами. Всюду мы оказываемся в затруднительном положении из-за некачественной геометрии или прямого попадания в вершину, где формально существует сразу два пересечения. В любом случае мы найдем четное число пересечений (ноль или два) и будем вынуждены сделать вывод о том, что пробная точка находится вне полигона, т.е. погрешить против очевидной истины. Чтобы поправить дело можно исходить из того, что представленные патологические случаи все-таки являются редкостью. Договорившись испускать луч в произвольном направлении с одинаковой вероятностью, мы должны заключить, что при разумной мере геометрических ошибок (эта мера должна быть близка к нулю), попадание в «нехорошие» зоны не должно происходить слишком часто. Если же таковое попадание случилось, то вместо попытки детального разбора обнаруженной патологии, связанного с выяснением ее нередко весьма причудливой природы, разумно было бы испустить новый луч, полагаясь на случай. Так можно продолжать бесконечно долго, но интуитивно понятно, что слишком много итераций нам не потребуется. Вопрос состоит лишь в том, как с алгоритмической точки зрения формализовать попадание в «нехорошие» зоны, которые мы договорились называть сингулярностями. Сингулярность — это эффект двоякой этиологии. С одной стороны он практически неизбежно порождается ошибками округления, связанными с конечнозначностью машинного представления иррациональных чисел. С другой стороны, невозможность точного стыка часто является результатом применения того или иного итерационного процесса, работающего с заданной точностью. Так, в общем случае нельзя найти аналитическую формулу для пересечения произвольных параметрических поверхностей, поэтому на практике вычислитель удовлетворяется некоторой разумной точностью, принося в жертву идеальность стыка и порождая вдоль него неизбежную патологию. Средство борьбы с такими патологиями известно довольно давно — толерантная геометрия.
Руководствуясь изложением [5], мы, вслед за Рекувичем, откажемся от алгоритма «наивного» испускания лучей в пользу более интеллектуальной процедуры классификации. Суть дела состоит в следующем. На первом этапе мы проверим, принадлежит ли пробная точка $p$ границе и, если да, то этим и удовлетворимся. В противном случае мы выпустим луч из пробной точки в произвольном направлении, вычисляя его пересечения со всеми гранями модели. В ближайшей точке пересечения мы должны будем удостовериться, что патологическую область удалось миновать и, если нет, то испустить новый луч. В случае же попадания в «хорошую» зону, мы проверим локальную окрестность точки пересечения и выясним, снаружи или внутри материала находится наша точка $p$. Следующий псевдокод формализует изложенное:
function Classify_Point_wrt_Solid(p, S)
{
for each face F of solid S do
{
if Point_IsOn_Surface(p, Surface(F)) then // Check host surface
{
// Classification without neighborhood
if Classify_Point_wrt_Face(p, F) == (in or on) then return on;
}
}
do forever
{
R = CastRay(p); // Pick a random ray
IntList = {}; // Empty set of intersections. Each intersection point is
// identified by its parameter along the ray and a specific
// "singularity" flag triggered if we find ourselves in a vertex
// or in interior of some edge
for each face F of solid S do
{
if not Ray_LiesOn_Surface(R, F) then
{
PList = Intersect_Ray_Surface(R, Surface(F)); // There can be many intersections
// in a curved case, so put all
// them into the list of parameters
for each point q in PList do
{
q_class = Classify_Point_wrt_FaceN(q, F); // Classification plus neighborhood (N)
if q_class == on then q.singular = true; // We fell on edge or vertex. Notice
// that we don't panic here as
// there is still a chance to find
// a non-singular point which is
// closer to p
else q.singular = false;
if q_class == (in or on) then Append(q, IntList);
}
}
}
if IntList is empty then return out; // No intersections for a good ray, so
// our point is outside
r = PointWithMinParameter(IntList); // Point with minimal u value
if r.singular then continue loop choosing another ray; // Panic: we do not want to
// deal with singularities
if Transition(r) == (in -> out) then return in else return out;
}
}
Нетрудно видеть, что этот алгоритм реализует своеобразное «бегство» от сингулярностей. Всякий раз, как мы попадаем впросак с очередным лучем, безо всяких попыток дополнительного разбора алгоритм «пугливо» (т.е. абсолютно произвольно «шарахаясь») выбирает новое направление. В нашей версии выбор направления происходит вслепую, хотя более продвинутые («менее паникующие») вариации алгоритма могли бы привлекать некоторую тактику «прицеливания», ориентируясь на фактическое расположение границ модели. Заметим, что предложенный алгоритм не «паникует» в случае если луч все-таки лежит на поверхности одной из граней. Мы видим, что такие грани пропускаются, т.к. касание одной грани должно неизбежно означать пересечение смежной с ней (рис. 18).
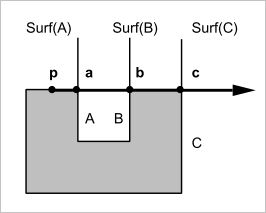
Рис. 18. «Бегство» от сингулярности в случае принадлежности луча грани.
Понятно, что, пропуская касательные грани, мы не упустим точки $a$, $b$ и $c$ из рассмотрения, так как рано или поздно они будут получены в итерациях по граням $A$, $B$ и $C$.
Выбор произвольного направления для испускаемого луча легко организовать через его сферические координаты, дважды используя генератор псевдослучайных чисел для углов $\phi$ и $\psi$ в интервале $[0, 2\pi]$ (рис. 19).
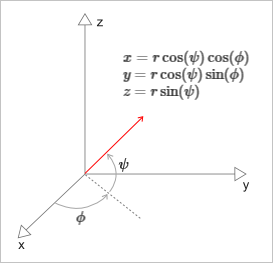
Рис. 19. Использование сферических координат дает простой способ испускания луча в произвольном направлении.
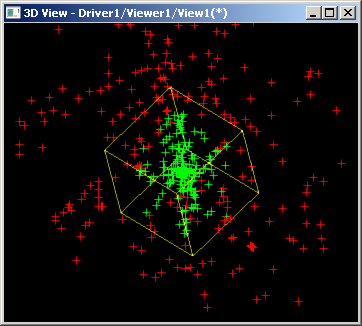
Рис. 20. Вычислительный эксперимент для предложенной схемы классификации точка-тело (среда Open CASCADE Technology). Зеленым цветом обозначены точки с принадлежностью $in$, красным — с принадлежностью $out$.
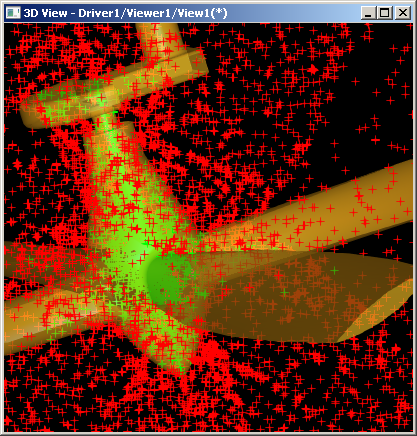
Рис. 21. Еще один вычислительный эксперимент для предложенной схемы классификации точка-тело. Используется тело сложной формы (среда Open CASCADE Technology). Зеленым цветом обозначены точки с принадлежностью $in$, красным — с принадлежностью $out$.
Классификация Ребро-Тело
Как было сказано ранее, мы свели проблему вычисления и слияния границ (boundary evaluation and merging) к задаче на ребрах, т.е. без явного привлечения классификации граней друг относительно друга. Последнюю классификацию мы заменяем классификацией ребер относительно результирующего тела $S$, для чего нам понадобится специальная процедура. Мы рассмотрели классификацию точки относительно тела, приведя для решения этой задачи простейший «пугливый» алгоритм, наделенный свойством произвольного выбора направления испускаемого луча классификации. Этот алгоритм будет играть роль «кирпичика» в классификации более сложного типа — ребра относительно тела. Именно эта, последняя, классификация подводит нас вплотную к реализации собственно булева алгоритма. Мы будем опираться на предложенную Рекувичем процедуру классификации типа Линия-Тело, псевдокод которой приведен ниже:
function Classify_Edge_wrt_Solid(E, S)
{
IntListNC = {}; // Empty set of intersections. Each intersection point is
// identified by its parameter along the edge, "singularity"
// flag, neighborhood and classification (NC) information
for each face F of solid S do
{
if not Curve_LiesOn_Surface(Curve(E), Surface(F)) then
{
PList = Intersect_Curve_Surface(Curve(E), Surface(F)); // There can be many intersections
// in a curved case, so put all
// them into the list of parameters
for each point p in PList do
{
p_class = Classify_Point_wrt_FaceN(p, F); // Classification plus neighborhood
if p_class == (in or on) then Append(p, IntListNC);
}
}
} // Loop by faces
if IntListNC is empty then
{
// No intersections, so E is entirely in, on or out. We pick an arbitrary
// point of E and classify it
q = SelectPt(E);
// Classify this point against solid
return Classify_Point_wrt_Solid(q, S);
}
// If we are here, then the intersection list is not empty. The points from
// this list will be used to check their associated transition values. Let's
// enrich the working list with extremities having Unknown neighborhoods
Append(E.FirstVertex, IntListNC);
Append(E.LastVertex, IntListNC);
// Sort the points by their parameters along the edge's curve
Sort(IntListNC);
// Remove duplicated points
RemoveDuplications(IntListNC);
// Bind membership information to each intersection point
for each point p in IntListNC do
{
if p.Nbh == unknown then p.Membership = unknown
else
{
// Assess transition and associate the corresponding membership
// information with our current point
transition = Transition(p);
if ( transition == (in, out) or (out, out) )
p.Membership = out;
else if ( transition == (out, in) or (in, in) )
p.Membership = in;
else
p.Membership = unknown;
}
} // Loop by intersection points
// There can be some points with unknown classification just because
// these points correspond to singularities at vertices. If E intersects
// the solid in a vertex, we agree to set unknown classification to such
// points
for each point p in IntListNC and point p_next as next and excluding last do
{
if p.Membership == unknown then
{
q = MidPoint(p, p_next);
p.Membership = Classify_Point_wrt_Solid(q, S);
}
}
// Neighborhood information is not useful anymore
CleanNeighborhood(IntListNC);
// Return classification results
return IntListNC;
}
На начальном этапе процедура ищет точки пересечения ребра со всеми гранями. При этом случай, когда геометрия ребра оказывается вложенной в геометрию грани, представляет опасность для численных методов поиска пересечений, поскольку пересечением будет являться континуум точек. Во избежание этих неприятностей, алгоритм проверяет наличие наложений между ребром и гранями с тем, чтобы оставить такие сингулярности без внимания. Так же, как и в случае классификации Точка-Тело, мы не упустим, действуя подобным образом, точки пересечения, т.к. найдутся смежные грани, где сингулярность отсутствует. Все точки пересечения помещаются в список вместе со своими окрестностями, которые будут нужны на этапе вычисления граничных переходов. Заметим также, что на этом этапе необходимо вычислить касательный вектор кривой ребра в каждой найденной точке пересечения. Касательный вектор укажет направление обхода ребра, что является существенным для правильной маркировки граничных переходов. Случай, если ни одна точка пересечения не была найдена, означает, что ребро находится либо полностью внутри, либо полностью вне тела. Этот случай обрабатывается проще всего: достаточно взять любую точку ребра и выполнить ее классификацию относительно тела.
На следующем этапе необходимо классифицировать каждую точку пересечения вдоль ребра согласно осуществляемому в этой точке граничному переходу. Предварительным этапом такой классификации является обогащение списка точек вершинами ребра, сортировка точек по параметру вдоль кривой и уничтожение дубликатов точек. Затем в каждой точке рассчитывается тип граничного перехода, в соответствии с которым точка получает собственный классификатор принадлежности, указывающий, вовнутрь или вне тела попадает ребро, будучи проходимым в направлении своей натуральной ориентации. По сути основная работа сделана: ребро разбито на однородные сегменты, вдоль каждого из которых справедлив тот или иной классификатор. Однако в завершении алгоритм отрабатывает еще один специальный случай, связанный с попаданием ребра в вершину. В этом случае простейшим выходом из ситуации будет рассмотрение другой точки, лежащей посередине между вершиной и следующей точкой пересечения.
В итоге алгоритм возвращает список классифицированных точек, задающих разбиение оригинального ребра по признаку принадлежности его сегментов телу.
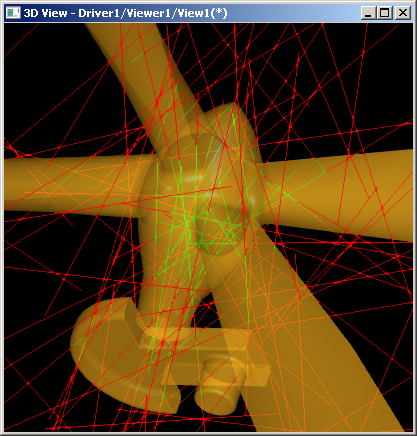
Рис. 22. Вычислительный эксперимент для предложенной схемы классификации ребро-тело. Используется тело сложной формы (среда Open CASCADE Technology). Зеленым цветом обозначены сегменты с принадлежностью $in$, красным — с принадлежностью $out$.
Комбинирование классификаций
Без рассмотрения осталась функция Combine_Classifications, которая должна распознать принадлежность ребра телу $S$ притом, что известна его принадлежность как телу $A$, так и телу $B$. Указанные известные принадлежности получаются следующим образом:
- Для собственных ребер $A$ принадлежность к $A$ есть заведомо $on$.
- Для собственных ребер $B$ принадлежность к $B$ есть заведомо $on$.
- Для собственных ребер $A$ принадлежность к $B$ ищется функцией Classify_Edge_wrt_Solid.
- Для собственных ребер $B$ принадлежность к $A$ ищется функцией Classify_Edge_wrt_Solid.
- Для ребер пересечения принадлежность к $A$ и $B$ нам не понадобится, т.к. эти ребра по построению автоматически должны войти в результат. Выше, однако, мы сделали несколько замечаний по поводу тонкостей работы с такими ребрами.
Займемся теперь непосредственно комбинированием классификаций. Допустим, что нам известны две тройки множеств: $(XinA, XonA, XoutA)$ и $(XinB, XonB, XoutB)$. Требуется получить тройку $(XinS, XonS, XoutS)$ притом, что $S = A \otimes B$. Таким образом мы желаем вывести классификацию ребер для тела $S$, зная классификации ребер для операндов. В [5] Рекувич отмечает, что комбинирование классификаций является «фундаментальным алгоритмическим инструментом» для задач вычисления и слияния границ. Он же отсылает читателя к работам Тилаува [13] за детальным обсуждением проблематики.
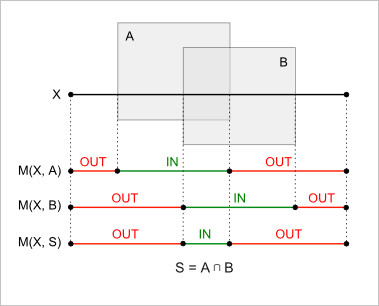
Рис. 23. Комбинирование классификаций для операции пересечения тел.
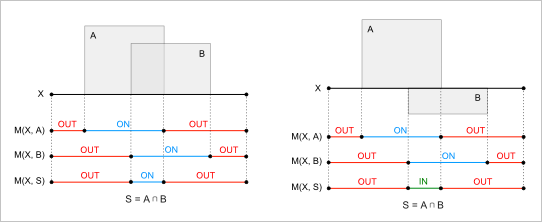
Рис. 24. Комбинирование классификаций для операции пересечения тел.
Из предложенного примера видно, что для операции пересечения $S = A \cap B$:
- $XinS = XinA \cap^* XinB$
- $XoutS = X \setminus^* XinS$
Таким образом, комбинирование классификаций может осуществляться вдоль параметрического интервала каждой из кривых. Именно это обстоятельство послужило основной причиной, почему мы отказались от классификации граней относительно тела и свели задачу к классификации ребер. Выше мы, однако, видели, что ситуация становится качественно сложнее в том случае, если границы объектов накладываются друг на друга. Если такие ситуации реализуются, то простым комбинированием логических признаков $in$, $on$ и $out$ нам уже не обойтись, и требуется привлекать также чисто геометрическую информацию о поведении окрестностей.
Что же Add_To_BRep?
Эта функция не получила сколько-нибудь обстоятельного описания в работах Рекувича, однако ее значение нельзя недооценивать. Дело в следующем. Мы видели, как, используя различные классификаторы, можно получить своеобразный суп из ребер, раскрашенных «цветами» $in$, $on$ и $out$. Эти ребра возникали в результате пересечения граней, а также претерпевали разбиение на сегменты в результате классификации. Рассмотренные нами алгоритмы образуют главную часть булевой операции. Эта часть подобна лесорубу, который выбирает сосны для строительства деревянного дома, готовит бревна и сбрасывает их в кучу. Функция Add_To_BRep в предлагаемой схеме должна осуществлять складывание бревен в итоговую постройку, то есть обеспечивать выбраковку, сортировку и подгонку по месту. В этом отношении все выглядит весьма логично. Однако в данной схеме серьезные требования предъявляются к лесорубу. Он должен подготовить бревна так, чтобы в процессе сборки дома не пришлось рубить дополнительные деревья. Ошибок быть не должно. Строительного материала должно хватить: алгоритм не предполагает повторной классификации.
Высокие требования к подготовительному (и в то же время основному) этапу булева алгоритма на практике могут привести к существенному усложнению вычислительной схемы. Отметим это и завершим пока описание вычислительной схемы Рекувича. В будущих заметках мы вернемся к обсуждению обработки сингулярностей для этого класса алгоритмов. Отметим основные свойства предложенной схемы:
- Сердцем схемы является пересечение кривых и поверхностей. Пересекаются всегда кривые с кривыми и поверхности с поверхностями.
- Накопление ребер — последовательный процесс. Должна быть гарантия, что накопленного материала хватит для конструирования итоговой модели.
Толерантный булев алгоритм
Мы видели, что строительным блоком алгоритма Рекувича является ребро, причем на всех этапах схемы мы выясняем, не реализовалась ли ситуация сингулярности. Если сингулярность имеет место, то алгоритм избегает ее обработки, так как геометрия в области сингулярности локально плохо определена или не определена вовсе. Обработка таких «плохих» зон оказывается проблемой повышенной сложности. Особенно это относится к тем алгоритмам, которые изначально были спроектированы для «точной геометрии», то есть таким, где мера сингулярных случаев считается равной нулю. В такой постановке все сингулярные случаи получают статус особых, а алгоритм вынужденно реализует некоторые побочные ветви вычислений, иногда плохо коррелирующие с руководящей идеей алгоритма. Так, при некоторых обстоятельствах может потребоваться изменение «пугливого» поведения алгоритма Рекувича, то есть внедрение специальных функций обработки сингулярностей, что, вообще-то, плохо укладывается в рассмотренную нами схему. Но есть и другая, с позволения сказать, «школа» булевых операций, которая предлагает обобщенную постановку вопроса об отношениях геометрических объектов.
С точки зрения этих, других, алгоритмов никаких сингулярностей нет. При этом необходимо использование так называемой «толерантной геометрии», то есть расширенного описания B-Rep, где к чисто геометрической информации добавляется информация о неточности — «толеранс» (или «допуск»). Толеранс нужен для того, чтобы придать не имеющей геометрического истолкования сингулярности геометрическое обличие, как правило, примитивное. Так, с вершиной связывается шаровая окрестность, центром которой является сама вершина, а содержимое внутренности шара нам безразлично. Ребро «раздувается» до трубки, внутри которой это ребро может совершать какие угодно осцилляции и даже иметь самопересечения — для нас это опять-таки не имеет значения — мы работаем с самой трубкой. Аналогично, грань приобретает толерантный слой, превращаясь из бесконечно тонкого листа в актуально тонкую пластину. Что же булев алгоритм?
Реализуемая над толерантными объектами, булева операция получает дополнительную свободу. Речь идет прежде всего о свободе от сингулярностей. Действительно, куда бы ни был испущен луч в схеме Рекувича, мы попадаем в зону, где геометрия, если и не определена точным математическим выражением, то во всяком случае застрахована объемлющей толерантной областью. Заметим здесь, что для выяснения отношений между объектами уже нельзя рассуждать в терминах только кривых и только поверхностей, как это делалось выше. В действительности для толерантного моделирования имеет значение лишь взаимное расположение толерантных объемов (шариков, трубок и слоев). В этом и состоит ключевое отличие толерантной булевой схемы от алгоритмов типа Рекувича. Для толерантной булевой операции строительным блоком является уже не только ребро или поверхность, но обобщенный толерантный объем, что приводит к необходимости рассмотрения следующих взаимных пересечений (подробнее см., например, [17]):
- Вершина — Вершина,
- Вершина — Ребро,
- Вершина — Поверхность,
- Ребро — Ребро,
- Ребро — Поверхность,
- Поверхность — Поверхность.
Следует держать в уме, что под пересечением здесь всегда понимается пересечение толерантных объемов, поэтому фраза «вершина пересекается с вершиной» не должна смущать читателя. Чтобы подчеркнуть это важное отличие между точным и толерантным пересечением иногда используется английское слово «interaction» — взаимодействие. В библиотеке Open CASCADE Technology принят собственный жаргон, и там тот же смысл вкладывается в слово «интерференция».
Интерференция — это влияние одной геометрии на другую. Результат этого влияния проявляется на границах исходных моделей локально, т.е. затрагивая, вообще говоря, не всю границу, а только ее часть. Кроме этого свойства локальности, интерферирующие области могут иметь различные типы, в зависимости от того, какие конкретно топологические объекты вступают в отношение интерференции. Для обогащения исходного граничного представления модели информацией об интерференциях, булев алгоритм может использовать вспомогательные структуры данных. Так или иначе, всякая интерференция должна быть решена. Разрешение интерференции может происходить по-разному, в зависимости от ее типа. Так, в случае пересекающихся ребер необходимо образовать в зоне взаимодействия толерантных объемов новую вершину. В случае же взаимного наложения ребер разумно будет построить новое ребро, «отбив» его двумя вершинами по границам зоны наложения. Если интерференция не может быть разрешена в силу тех или иных причин, то алгоритм завершается с ошибкой.
Заключение
Как было отмечено ранее, создание надежного булева алгоритма — нетривиальная задача, решение которой практически никогда невозможно считать исчерпывающим из-за обилия патологических случаев, возникающих в реальной инженерной практике. Следует сказать, что введение толерантной геометрии не есть панацея. Отказавшись от пугливой стратегии бегства от сингулярностей, мы вывели на сцену альтернативный аппарат толерантного моделирования и получили взамен новую проблему разрешения интерференций. Достаточно сказать, что не все интерференции разрешаются легко (слово «легко» при должном уровне скептицизма можно убрать из этого предложения).
В работе [5], которой мы уделили так много внимания, возникает тот же принципиальный вопрос. Что лучше: работать с сингулярностями или избегать их? Рекувич задает этот вопрос, но с честностью настоящего ученого оставляет его открытым. В 1984 году геометрическое моделирование еще не было таким развитым, каким мы находим его сегодня. Однако и теперь, насколько нам известно, ничего определенного по поводу сравнения двух подходов сказать нельзя. Конечно, наш вопрос — не проблема тысячелетия. Кроме того, уже интуитивно ясно, что ответ едва ли может быть получен без четкой формализации понятия патологии. Так или иначе, критерии точности, надежности и эффективности должны быть руководящими в нелегком деле создания оптимального булева алгоритма.
- [1] C. Hoffmann. Geometric and Solid Modeling. — 2002
- [2] M.C. Arruda. Boolean Operations on Non-Manifold and B-Rep Solids for Mesh Generation. — 2006
- [3] R. Rossignac, A.G. Requicha. Solid Modeling // Review article. — 1994
- [4] A.G. Requicha. Geometric Modeling: A First Course, Fundamental Algorithms
- [5] A.G. Requicha, H.B. Voelcker. Boolean Operations in Solid Modeling: Boundary Evaluation and Merging Algorithms // Technical Memorandum. — 1984
- [6] Н. Снытников. Эволюционное и революционное будущее геометрических 3D-ядер // isicad.ru. — 2013
- [7] M. Mantyla. An Introduction to Solid Modeling. — 1988
- [8] J. Keyser, T. Culver, M. Foskey, S. Krishnan. ESOLID — A system for exact boundary evaluation. — 2004
- [9] S. Krishnan et al. BOOLE: a Boundary Evaluation System for Boolean Combinations of Sculptured Solids. — 2001
- [10] S. Krishnan, M. Gopi, D. Manocha, M. Mine. Interactive Boundary Computation of Boolean Combinations of Sculptured Solids. — 1997
- [11] L. Piegl, W. Tiller. The NURBS Book
- [12] Н. Голованов. Геометрическое моделирование
- [13] Tilove. Set membership classification: A unified approach to geometric intersection problems
- [14] D. E. Weisberg. The Engineering Design Revolution: The People, Companies and Computer Systems That Changed Forever the Practice of Engineering
- [15] Черепашков А.А. Методы и средства обучения автоматизированному проектированию в машиностроении
- [16] A. Requicha and H. Voelcker, the 2007 Pierre Bezier Award Recipients, http://solidmodeling.org/bezier-award/a-requicha-and-h-voelcker/
- [17] D. Jackson. Boundary representation modelling with local tolerances // Parasolid Business Unit, EDS Unigraphics. — 1995