A long note on prototyping
For the past few months I have been working on a couple of prototypes without any clear specification at hand. One was related to bend sequence planning in sheet metal, and another was (and still is) about generating technical drawings. While these topics have almost nothing in common from the algorithmic perspective, I have found myself exploiting a somewhat similar prototyping strategy. Here is the thing.
When you start developing something geometric for the first time, you might have only a fuzzy idea on what the result should actually be looking like. This is where you normally start prototyping, i.e., trying this and that with the goal to improve your own understanding of the problem and increase the chances to solve it. Prototype is so important that 8 years ago we started our Analysis Situs project that was supposed to serve as a workbench for the newly developed algorithms. That was our key idea for transitioning from academia to industry. This idea is nothing new, of course, and the same principle can easily be identified behind the OpenCascade's native DRAW app. Analysis Situs was supposed to take over the idea of DRAW and develop it further. It is not me to decide whether it was success or not, but it is safe to say that our team is using Analysis Situs productively exactly for this sole purpose: to prototype a thing.
Architecturally, Analysis Situs offers the following tools to facilitate prototyping:
- Extendable data framework (ActiveData) for presenting new domain-specific objects without redeveloping the entire app.
- Imperative plotter.
- VTK-ActiveData bridge whose history can be traced decades back, when we developed some commercial pre-/post-processors under the umbrella of OCC company.
- Reusable tools and classes, too many to list them here.
Imperative plotter is basically the same idiom as the one used behind `DrawTrSurf` and `DBRep` classes of OpenCascade. This is nothing than a visual debugging facility, just a graphical counterpart for C++ `cout`. It appeared so handy over the years that almost every algorithm I developed myself was enriched with the imperative plotter diagnostic tool from the day one.
What I rather realized these days was that I barely use other powerful prototyping idioms, namely points 1 and 3 in the list above (i.e., the customization of the data model). To go further, I'll take this drawing generation app as an illustration. Let's suppose we have a flat shape representing an unfolded sheet metal part. What we want to know is all characteristic distances over this flat shape to be able to put together a PDF drawing. A technical drawing is a composition of a geometric view (or views), annotations, legends and frames. And the most important part of a drawing is, of course, the geometry with dimension lines. Something like this:
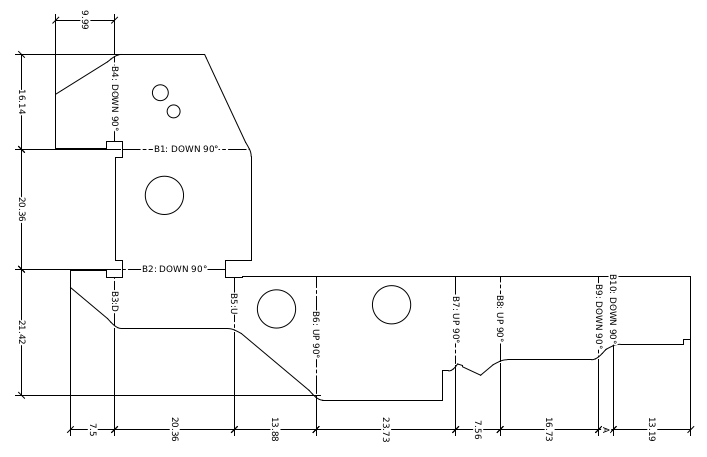 |
Computationally speaking, to generate a drawing, you must perform a sequence of geometric measurements. In sheet metal, it could be the distance between two bends, or the distance between a bend line and the boundary. When you look at a drawing, you can easily tell if some dimensions are off, but at the level of computing, everything is just a number. A prototyping framework should aid in matching numbers with visuals, and this is where custom data models can help.
 |
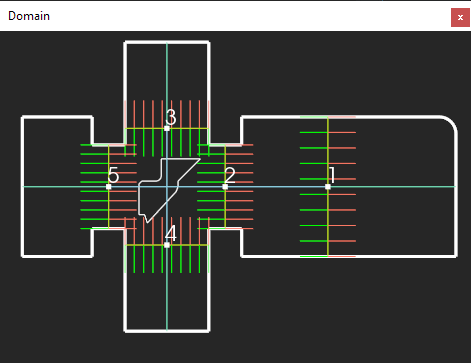
According to the visualization architecture of Analysis Situs, each rendered presentation corresponds to a persistent OCAF data object. There is a bunch of predefined object types, including curves, surfaces, vectors, point clouds and shapes. These objects serve as a backbone for the imperative plotter. Although primitive entities can be used to render a variety of things, it is typically far better to generate bespoke types for your domain-specific objects. In our example with drawings, we may introduce specific types for matters like a bend line and its accompanying measurement. This is object-oriented design, a well-known principle with one notable distinction that its primary objective is to better organize your computations.
 |
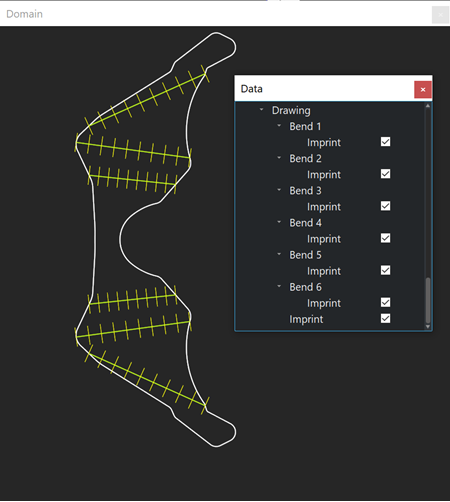
Object-oriented design changes the way of thinking. The algorithm becomes more data-centric, focusing on how to populate a specific data structure rather than the computation mechanics as such. In some ways, the data structure you are about to populate absorbs some of the intrinsic complexity of the algorithm and rebalances the "data vs computation" burden. The picture below is another illustration for dimensioning on a sheet metal part. A flat pattern is represented with a two-dimensional drawing (living in the "UV" space of a reference plane). Each bend line is rendered as a hedgehog glyph that indicates the "positive" (red) and "negative" (green) measurement directions. Notice that the bend lines are numbered, so it is easy to match them up with the corresponding OCAF data object (that uses the same index in its name).
 |
This prototype is not intended for use in production. Its sole objective is to provide you (as a programmer) with enough graphics to easily maintain your algorithm without having to spend many desperate hours debugging numbers. What is especially important about persistent objects is that using them, you do not have to think too carefully about somewhat strongly optimized data structure. Neither should you think about the structure of your algorithm too early. You just organize the place where your data is stored and draw it on the screen. That is totally fine at prototyping phase.
Someone smart said once that if you are about to take down a tree, you'd better spend 90% of time sharpening your axe. That's basically the entire idea behind preparing a prototyping workbench: you do it once and then enjoy your computation.
Want to discuss this? Jump in to our forum.