Несимметричные трубки в Open CASCADE Technology
В заметке о моделировании трубки мы рассмотрели вариант с переменным радиусом сечения. Попробуем расширить возможности этого подхода, а заодно понять, как оно работает в целом.
Работать будем с пакетом GeomFill библиотеки TKGeomAlgo. Эта библиотека содержит основные геометрические алгоритмы OCCT. TKGeomAlgo — своеобразное сердце системы в ее геометрической ипостаси. В ней находятся инструменты пересечения кривых и поверхностей, утилиты аппроксимации, собственно моделирования (на низком уровне) и прочее. Нам потребуется класс GeomFill_Sweep, который реализует кинематическое построение поверхности, то есть протягивание профиля вдоль траектории. В предыдущем примере мы работали с сечением в виде окружности, заставляя его менять радиус по ходу «движения». При этом мы заметили, что ни о каких радиусах GeomFill_Sweep не знает, и что в действительности мы имеем скалирующее преобразование общего вида. Использованный нами подход замечательно работает, если мы хотим сохранить симметрию профиля относительно траектории. Однако иногда инженеру требуется больше свободы. Так возникает задача на построение несимметричной трубки, то есть тела, не дающего в разрезе окружность. Будем считать, что термин «трубка» к такого рода телам все еще применим, хотя бы ради удобства.
Инициализация GeomFill_Sweep, требует задания двух так называемых «законов»: закона изменения сечения (section law) и закона положения (location law). Первый выражает эволюцию сечения вдоль траектории. Эволюция в нашем случае означает скалирование, причем оно осуществляется в локальных координатах сечения (часто — в плоскости эскиза). Второй закон (закон положения) погружает сечение в трехмерное пространство моделирования, привязывая его к каждой точке вдоль траектории и ориентируя нужным образом. Стандартный способ ориентации дает так называемый трехгранник Френе, сопровождающий траекторию. Полный листинг инициализации GeomFill_Sweep был дан ранее, поэтому ограничимся небольшой выжимкой, где эти законы вводятся:
Handle(GeomFill_SectionLaw) sectionLaw = ... Handle(GeomFill_LocationLaw) locationLaw = ... // Construct sweep GeomFill_Sweep Sweep(locationLaw, 0); ... Sweep.Build(sectionLaw, ...);
Нетрудно догадаться, что это довольно мощный механизм. Путем наследования мы можем определить свои законы сечения и положения (section law, location law), получив тем самым больше свободы для формообразования. Например, можно смоделировать что-то совершенно бессмысленное:

Но можно пойти и осмысленным путем. Мы знаем, что классическая трубка обладает симметрией. Эта симметрия чаще всего выражает истинное намерение проектировщика (design intention), поэтому считать ее ограничением было бы странно. Как минимум, это полезное ограничение. Но полезным бывает и нарушение симметрии, например, в задачах оптимизации. Допустим, что требуется рассчитать оптимальную форму воздуховода, не ограничивая пространство решений только его симметричными формами. Конечно, здесь можно обойтись без кинематического моделирования вовсе, но это усложняет задачу построения формы.
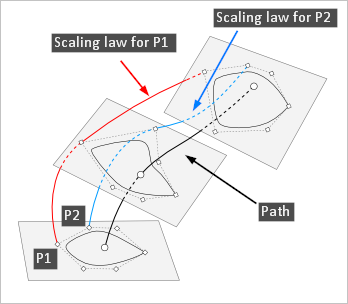
Когда мы говорим о симметричной трубке, мы имеем в виду изотропное скалирование сечения вдоль траектории. До сих пор мы ограничивались единственным законом, который описывал, как изменяется скалирующий множитель, то есть как траектория «притягивает» и «отталкивает» сечение. Запрограммировать такую эволюцию позволяет класс GeomFill_EvolvedSection, который мы и использовали в упражнении раньше.
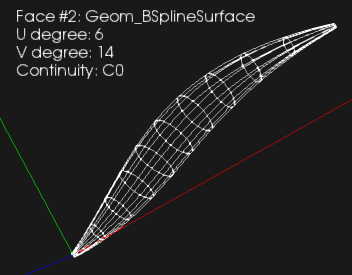
Теперь усложним задачу. Будем считать, что сечение задано не окружностью, но сплайновой кривой. Так, если мы имеем окружность, то ее предварительно нужно сконвертировать в NURBS-представление.
// Let's convert our circle C to b-curve BC Handle(Geom_BSplineCurve) BC = GeomConvert::CurveToBSplineCurve(C, Convert_QuasiAngular);
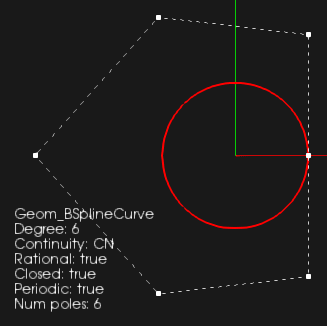
В результате такого преобразования мы получаем рациональную периодическую кривую шестой степени с шестью контрольными точками. Постараемся на этот факт опереться. Пусть у каждой контрольной точки есть свой индивидуальный скалирующий закон. В этом случае мы имеем неизотропное масштабирование, нарушающее круговую симметрию сечения. Это нам и нужно.
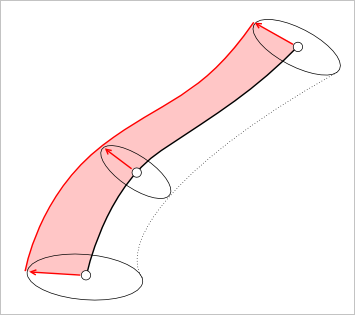
Следует явно оговорить одно важное обстоятельство. Оно состоит в том, что в результате скалирования (изотропного или нет) сечение никогда не перестанет быть плоским (если, конечно, оно изначально было плоским). Это происходит из-за того, что скалирование работает в локальных координатах сечения, безотносительно его привязки к траектории и реперу Френе. Это действительно очень хорошее свойство, так как контрольные точки сечения в своем движении относительно траектории будут иметь всего одну степень свободы (вместо трех в общем случае некинематического моделирования). Меньше степеней свободы — меньше шансов испортить форму. Кроме того, выше было вскользь упомянуто о задачах оптимизации для САПР. Так вот, ограничение степеней свободы снижает размерность задачи оптимизации: вместо трех координат $X$, $Y$, $Z$ для каждой контрольной точки мы имеем дело с единственным скалярным множителем.
Чтобы смоделировать неизотропное масштабирование контрольных точек, нам нужно унаследовать новый тип от GeomFill_SectionLaw. Назовем наш класс MorphedSection.
DEFINE_STANDARD_HANDLE(MorphedSection, GeomFill_SectionLaw)
//! This law gives each control point a freedom to evolve independently.
class MorphedSection : public GeomFill_SectionLaw
{
public:
// OCCT RTTI
DEFINE_STANDARD_RTTI(MorphedSection, GeomFill_SectionLaw)
public:
MorphedSection(const Handle(Geom_Curve)& C,
const NCollection_Sequence<Handle(Law_Function)>& Laws);
virtual Standard_Boolean
D0(const Standard_Real Param,
TColgp_Array1OfPnt& Poles,
TColStd_Array1OfReal& Weigths);
...
Для экономии места в приведенном листинге я оставил только две принципиально важные функции: конструктор и метод D0. Конструктор принимает кривую сечения и набор законов, ассоциированных с каждой контрольной точкой. Для окружности, преобразованной в NURBS-кривую, количество таких законов должно равняться шести. Метод D0 задает собственно эволюцию сечения. Приведем его код:
Standard_Boolean MorphedSection::D0(const Standard_Real U,
TColgp_Array1OfPnt& Poles,
TColStd_Array1OfReal& Weights)
{
myCurve->Poles(Poles);
for ( Standard_Integer ii = 1; ii <= Poles.Length(); ++ii )
{
const Standard_Real val = myLaws(ii)->Value(U);
Poles(ii).ChangeCoord() *= val; // Magic here!
}
myCurve->Weights(Weights);
return Standard_True;
}
Этот код почти полностью повторяет вычисления, производимые в оригинальном GeomFill_EvolvedSection (откуда все и было, в общем-то, скопировано). Разница лишь в том, что здесь мы выбираем скалирующий множитель для каждой контрольной точки отдельно. Реализация метода D0 позволяет нам строить поверхность качества C0. Для обеспечения лучшей гладкости потребуется также реализовать методы D1 (гладкость порядка C1) и D2 (гладкость порядка C2). Понятно, что стремиться нужно именно к гладкости порядка C2. Ниже приведен результат моделирования трубки с одновременным применением двух различных законов скалирования:

Если вы возьметесь немного поэкспериментировать, то довольно скоро обнаружите проблему. Несмотря на запрошенную гладкость результата C2, итоговая поверхность часто страдает вполне очевидными изломами. Об их наличии можно судить визуально, не привлекая никакой аналитики.

Это серьезно портит дело.

Но причина, вообще-то, очевидна. Достаточно посмотреть на то, как выглядит сплайн эквивалентный окружности (как вы помните, мы начали с преобразования окружности в NURBS-кривую). Мы видим, что стартовая контрольная точка принадлежит кривой (кратность соответствующего узла здесь равна степени B-сплайна). Следовательно, любое шевеление контрольной точки неминуемо приведет к образованию острого края, что мы и наблюдаем на итоговой поверхности.
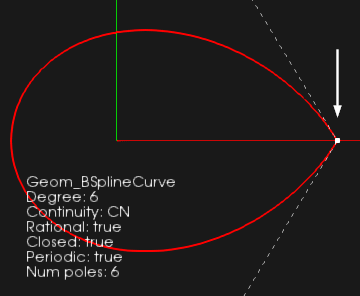
Чтобы предотвратить этот паразитный эффект контрольные точки номер 2 и 6 должны двигаться согласовано с контрольной точкой 1. А именно, сегменты 1-2 и 6-1 всегда должны оставаться параллельными.
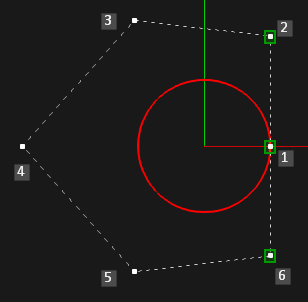
Выходит, что законы эволюции, ассоциированные с оригинальными контрольными точками, вообще-то зависимы. Правда, это касается только контрольных точек 1, 2 и 6. На остальные ограничений нет.
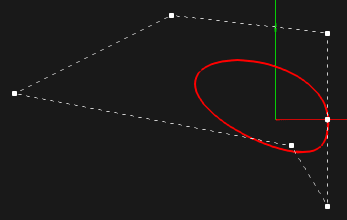
Связь между точками нетрудно вывести. Выражаясь словами А. А. Андронова, это «дико тривиальная тригонометрия». Заметим, что скалирование оставляет неизменным угол $\phi$ между векторами контрольных точек $v_1$, $v_2$ и $v_3$.
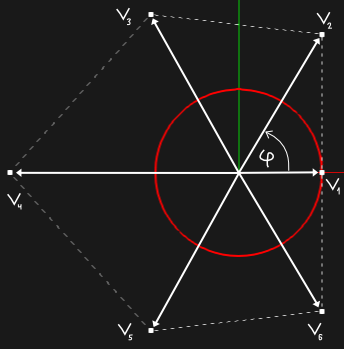
Из условия параллельности сегментов мы получаем, что законы скалирования точек 1, 2 и 6 должны совпадать. Другой вариант — позволить углу $\phi$ изменяться, но это будет уже не скалирование (хотя такой случай тоже представляет интерес). Зафиксировав в трех точках одинаковые законы, мы обеспечиваем гладкость результата не хуже C2.
