Автоматический реинжиниринг объектов свободной формы (часть 1)
"Mesh data is so important for so many reasons. It is how things are displayed by a graphics card, the format is used in medical imaging, games, movie making, allowing morphing shape transitions, FEA and other simulations. This kind of data has to be able to be integrated into engineering data, in fact, we really need to be able to use mesh as engineering data. But obviously, we need NURBS accuracy for manufacturing.
If we had good enough tools, we could work the entire model as a mesh model, and then output it as NURBS as needed. The mesh workflow more closely resembles direct edit than history-based modeling, but mesh has more sophisticated selection tools to allow different types of edits. NURBS/mesh fluidity would allow all sorts of topological edits that haven’t been available before."
(source)
Введение
Воссоздание точной цифровой модели объекта из неполного описания его геометрической формы остается актуальной инженерно-конструкторской проблемой [1]. Задачами реконструкции занимается дисциплина, известная как обратный инжиниринг (реинжиниринг) или DSR (Digital Shape Reconstruction). Ключевым этапом промышленного реинжиниринга является моделирование геометрической формы объекта в виде его граничного представления (boundary representation, B-Rep) [2], исходя из заданного облака точек, либо полигональной сетки. Криволинейное граничное представление является, на сегодняшний день, стандартом де факто для систем автоматизированного проектирования (САПР). Как отмечают авторы обзора [1], CAD-модель (в граничном представлении) является своеобразным «языком», на котором общаются различные средства автоматизации проектирования и производства. Существенной проблемой, поэтому, является обеспечение совместимости различных инженерных программных сред, и реинжиниринг здесь может рассматриваться как одна из типовых подзадач.
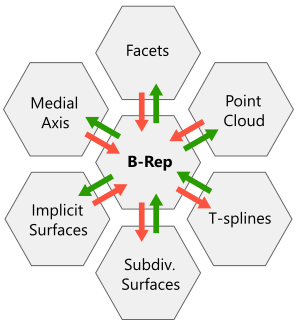 |
Ключевая роль граничного представления в инженерном ПО. Стрелками показано преобразование из одной схемы представления геометрической модели в другую. Цвет стрелки соответствует сложности преобразования (красный — проблемная область, зеленый — типовые алгоритмы). |
В инженерной практике задачи реконструкции имеют различные истоки. Например, если объект создавался без использования САПР, то его цифровое представление отсутствует изначально. Иногда геометрическая модель оказывается недоступна в силу иных причин, таких как устаревание или исчезновение оригинальной CAD-системы. В таких случаях целью реинжиниринга является получение ранее не существовавшей или утраченной цифровой модели. Восстановленная геометрия может использоваться для дальнейшего редактирования CAD-модели, автоматизированного изготовления детали на станке с ЧПУ, а также для решения частных расчетных задач (исследование прочности, термический анализ, аэродинамический анализ и т.д.) или параметрической оптимизации формы. Если параметрическая оптимизация осуществляется на полигональной модели, то проблема реинжиниринга может возникать при обратном переходе от деформированной сетки [3] к CAD-представлению. Подходы обратного инжиниринга находят применение и в качестве основного средства моделирования еще не существующих объектов [4]. Так, в автомобильной промышленности часто используется техника оцифровки физического макета, выполненного скульптором для демонстрации внешних обводов изделия. Иногда геометрическое моделирование выполняется изначально в полигональном виде, после чего реинжиниринг обеспечивает переход к точному граничному представлению [5]. В последнем случае, техники реконструкции играют, в сущности, ту же роль, что и традиционные техники моделирования «снизу-вверх» с той разницей, что вместо работы «с чистого листа» используется вспомогательная полигональная «подложка». Так или иначе, в задачах реконструкции инженер имеет дело с некоторым опорным геометрическим представлением в виде неупорядоченного или структурированного облака точек, либо поверхностной триангуляции. Опорная геометрия направляет процесс моделирования и служит для сопоставления целевой и воссозданной эталонной формы объекта.
В зависимости от целей обратного инжиниринга, можно рассмотреть различные критерии успешности процесса реконструкции. Например, при создании цифровой копии физического макета, требуется обеспечить минимальную геометрическую невязку между CAD-моделью и ее полигональным представлением. В автомобильной промышленности также предъявляются строгие требования к эстетическим качествам изделия, поэтому в процессе моделирования должны использоваться т.н. «поверхности класса А». С другой стороны, при воссоздании цифровой модели поврежденной детали, либо детали с большим износом, высокая точность реконструкции не только не требуется, но является нежелательной в тех пространственных зонах, где реальная форма существенно расходится с эталонной. Минимизация исключительно геометрической невязки приводит к тому, что результирующая модель оказывается лишенной таких ключевых качеств, как, например, осевая симметрия, параллельность или ортогональность граней и т.п. Таким образом, обратный инжиниринг есть многокритериальный процесс, в котором набор и строгость привлекаемых критериев регулируется в зависимости от конкретного индустриального приложения и планируемой технологии изготовления.
Идеальный реинжиниринг должен быть полностью автоматическим. С другой стороны, реальность такова, что без привлечения инженерной экспертизы реконструируемые объекты оказываются всего лишь геометрическими «артефактами», более или менее пригодными для решения узкого класса задач. Например, для реконструкции экстрерьера автомобиля важно не только обеспечить минимальную геометрическую невязку между данными оцифровки и итоговой моделью, но и дать внятное топологическое покрытие этой модели. Топология не выбирается произвольно, но очерчивает конструктивные элементы модели. На сегодняшний день, в такой постановке эта задача подсильна лишь квалифицированному инженеру. Даже респектабельные коммерческие пакеты, чья стоимость измеряется десятками тысяч долларов, не являются всесильными, в чем недавно убедился и автор этих строк. Более того, на рынке открытого программного обеспечения для решения задач промышленной (САПР) реконструкции не сделано ровным счетом ничего стоящего. Это и понятно, ведь реинжиниринг как таковой — проблемная область геометрического моделирования, в которой нет простых решений, а есть только комплексные. Грубо говоря, нельзя реализовать один «алгоритм реинжиниринга», который решит задачу геометрической реконструкции во всем ее многообразии. Скорее придется реализовать полновесную САПР, что и демонстрируют коммерческие игроки, такие как Geomagic или Mesh2Surface. Решение задачи реинжиниринга «по-взрослому» немыслимо без соответствующей научной деятельности, организуемой внутри R&D-подразделений коммерческих организаций или в рамках внешних исследовательских групп.
Реконструкция по сети кривых
Занимаясь реинжинирингом CAD-моделей, следует разграничивать определенные классы геометрических форм, диктующие, до известной степени, сам принцип реконструкции. Объекты, созданные природой, включая тело человека, имеют свободную форму, точное представление которой обеспечат NURBS, поверхности подразделения или T-сплайны. Объекты искусства, такие как скульптуры, в этом отношении похожи, поскольку и в них сложность формообразования не подчинена жестким ограничениям. Другое дело инженерные объекты, хотя и они бывают разными. Так, функциональные, т.е. сообразующиеся с аэродинамическим потоком, изделия, имеют свободную, но не произвольную форму. Лопатка турбины должна органично вписываться в поток, оставаясь притом технологичной. На другом конце этого условного спектра находятся типовые машиностроительные детали, чье формообразование наилучшим образом выражается канонической геометрией, т.е. плоскостями, цилиндрами, сферами, конусами и торами. Сюда же отнесем и токарные изделия, где не обойтись без поверхностей вращения. Охватить такое разнообразие в едином программном комплексе — задача не из простых.
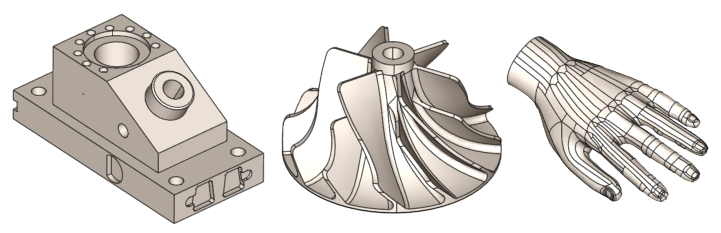 |
Различные типы геометрических объектов. Слева-направо: типовая машиностроительная деталь (ANC 101), рабочее колесо турбины, кисть человека. |
Мы рассмотрим т.н. скульптурные поверхности, в которых топология выбирается если не произвольно, то с минимальным количеством ограничений. Существующее открытое программное обеспечение позволяет приблизиться к решению задачи автоматической реконструкции на этом классе объектов (ниже мы увидим, как именно это делается). Начнем с цикличной схемы процесса реконструкции, каждый блок которой, вообще-то, соответствует целому ряду алгоритмов, применяемых или нет в зависимости от конкретной задачи.
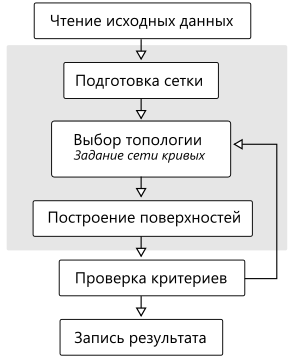 |
Блок-схема алгоритма реконструкции на сети кривых. |
Реконструкция начинается с чтения исходных полигональных данных, и здесь мы ограничиваемся STL как наиболее распространенным форматом описания фасетной геометрии. Исходная триангуляция, как правило, требует предобработки, такой как децимация (снижение количества полигонов), заполнение зазоров, устранение мелких деталей и т.п. Все эти операторы сами по себе нетривиальны, но их можно найти в открытых программных продуктах, таких как VTK, OpenMesh или MeshLab.
 |
Исходная триангуляция после децимации. |
Ключевым этапом процесса реконструкции является сегментация, то есть разбиение сетки на регионы, отвечающие различным конструктивным элементам изделия. Сегментация вручную — процесс затратный и требующий не только квалифицированного пользователя, но и специальным образом спроектированного ПО, по сложности интерфейса едва ли уступающего полновесной САПР. Привлекательной во всех отношениях, поэтому, выглядит полностью автоматическая реконструкция. Опубликованные в научных изданиях методы, такие как [6], не сопровождаются соответствующим программным обеспечением, а реализация подобных алгоритмов «с нуля» потребует больших усилий. В качестве компромиссного варианта, позволяющего сделать ретопологию «в лоб», мы выбрали программу Instant Meshes. С ее помощью осуществляется переход к сетке из четырехугольных элементов.
 |
Сетка из четырехугольных элементов, построенная программой Instant Meshes. |
Топология проецируется на исходную сетку, после чего каждое ребро аппроксимируется B-кривой. В результате имеем сеть кривых, заданных на триангуляции. Следующий этап состоит в заполнении каждой криволинейной ячейки B-поверхностью, для чего, в случае четырехугольных элементов, идеально подходят порции Кунса. Поверхности могут быть уточнены путем аппроксимации внутренних узлов триангуляции.
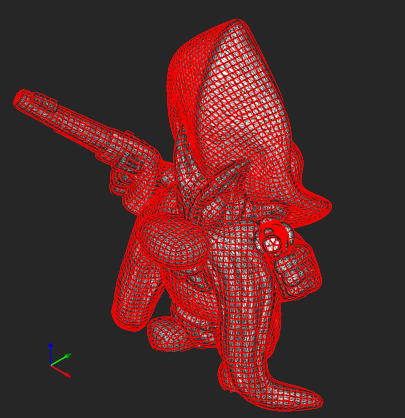 |
Сеть кривых на триангуляции. |
Использование четырехугольных элементов ретопологии позволяет ограничиться лоскутами B-поверхностей в натуральных границах, без обрезок. Это, в свою очередь, упрощает процедуру гладкого сопряжения для регулярных ребер (регулярное ребро — это такое ребро, каждая вершина которого имеет валентность, равную четырем).
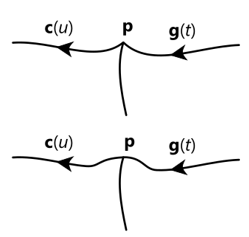 |
Модификация стыка кривых для обеспечения гладкости порядка G1. |
Особого внимания заслуживают нерегулярные ребра, но вопросом их гладкой стыковки мы займемся в другой раз.
Источники
- [1] Geng Z. and Bidanda B. Review of reverse engineering systems – current state of the art. Virtual and Physical Prototyping, vol. 12, no. 2, 2017, pp, 161-172.
- [2] Requicha A.G. Representations for Rigid Solids: Theory, Methods, and Systems. ACM Computing Surveys vol. 12, no. 4, 1980, pp. 437-464.
- [3] Sederberg T.W. and Parry S.R. Free-form deformation of solid geometric models. In Proc. of the 13th annual conference on Computer graphics and interactive techniques (SIGGRAPH’86), 1986, pp. 151-160.
- [4] Bradley C. and Currie B. Advances in the Field of Reverse Engineering. Computer-Aided Design and Applications, vol. 2, no. 5, 2005, pp. 697–706.
- [5] Gulanová J., Gulan L., Forrai M., and Hirz M. Generative engineering design methodology used for the development of surface-based components. Computer-Aided Design and Applications vol. 14, no. 5, 2017, pp. 642-649.
- [6] Eck, M. and Hoppe, H. 1996. Automatic reconstruction of B-spline surfaces of arbitrary topological type. Proceedings of the 23rd annual conference on Computer graphics and interactive techniques - SIGGRAPH '96, ACM Press, 325-334.